Triangle Angle Sum Theorem: Engaging Worksheet for Quick Learning

🎨 Note: The Triangle Angle Sum Theorem (or Triangle Sum Theorem) states that the sum of the three interior angles of a triangle is always 180 degrees.
Understanding the Theorem

The Triangle Angle Sum Theorem isn’t just a rule; it’s a cornerstone in understanding triangles. To grasp this concept:
- Define Triangle: A triangle is a polygon with three sides and three angles.
- Sum of Angles: The internal angles always add up to 180 degrees, regardless of the triangle’s shape or size.

This theorem applies to any type of triangle:
- Equilateral (all sides equal, all angles equal to 60°)
- Isosceles (two sides and angles are equal)
- Scalene (no sides or angles are equal)
Learning through Practice

Engaging in practice helps solidify understanding of this mathematical principle. Here are some interactive ways to learn:
- Paper Cutting Experiment: Draw a triangle on paper, cut it out, and tear off the corners. When placed together, they will form a straight line.
- Dynamic Geometry Software: Use software like GeoGebra to drag and alter triangles, watching the angles change yet sum to 180°.
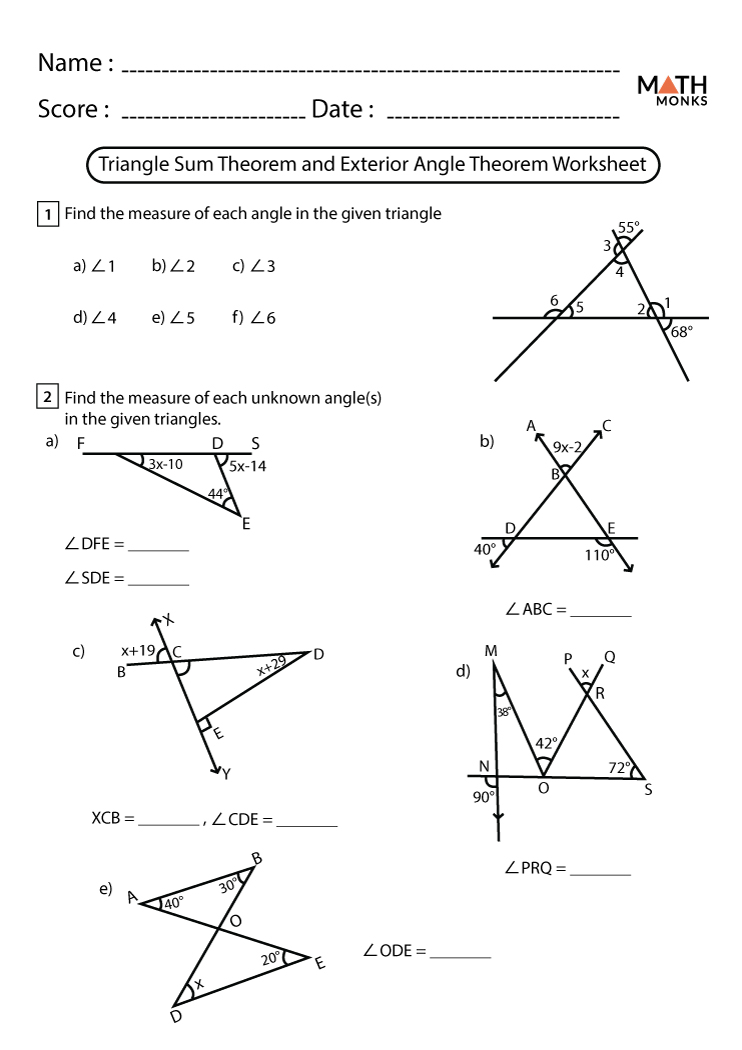
Worksheet for Quick Learning

To reinforce the Triangle Angle Sum Theorem, try this worksheet:
| Problem | Solution |
|---|---|
| Find the third angle in a triangle if the other two are 35° and 45°. | The third angle is 100° because 180° - (35° + 45°) = 100°. |
| Calculate the sum of the angles of an equilateral triangle. | The sum of angles in any equilateral triangle is always 180°. |
| If one angle of an isosceles triangle is 80°, what are the other two? | The other two angles would be 50° each, since (180° - 80°)/2 = 50°. |
| Verify that all angles of any triangle add up to 180°. | By drawing or measuring any triangle, you'll find the sum is indeed 180°. |

📐 Note: When performing the worksheet problems, pay attention to the type of triangle, as it can simplify angle calculations.
Real-Life Applications
The Triangle Angle Sum Theorem is not just theoretical; it has practical applications:
- Architecture: In designing structures, architects ensure that the angles of load-bearing triangles meet to distribute weight evenly.
- Navigation: Pilots and sailors use triangles in triangulation for locating positions or calculating distances.
Teaching the Theorem

Here are some tips for teaching the Triangle Angle Sum Theorem effectively:
- Visual Aids: Use diagrams and manipulatives to show how angles form a straight line.
- Hands-On Activities: Encourage students to cut out triangles or use protractors to measure angles firsthand.
- Group Work: Pair students to discuss and work through angle sum problems together, promoting collaborative learning.

Understanding the Triangle Angle Sum Theorem opens doors to further exploration in geometry and problem-solving.
Let’s summarize this journey through the Triangle Angle Sum Theorem:
- The theorem dictates that the sum of a triangle’s interior angles is 180°.
- This principle applies universally across all types of triangles.
- Engaging activities and worksheets help solidify this concept.
- Practical applications make the theorem relevant to real-world scenarios.
- Effective teaching methods enhance comprehension and retention of the theorem.
What is the Triangle Angle Sum Theorem?

+
The Triangle Angle Sum Theorem, also known as the Triangle Sum Theorem, states that the sum of the three interior angles of any triangle always equals 180 degrees.
Can this theorem be applied to all types of triangles?

+
Yes, whether a triangle is equilateral, isosceles, or scalene, the sum of its interior angles is always 180°.
How can I check the sum of angles of a triangle using a protractor?

+
To check, measure each angle of a triangle with a protractor. Add these measurements together, and the total should be close to 180° (within the precision of your protractor’s accuracy).
What are some practical applications of the Triangle Angle Sum Theorem?

+
The theorem is used in architecture for designing structures, in navigation for triangulation, and in many other fields where understanding the geometry of triangles is essential.
Why is it important to learn about the Triangle Angle Sum Theorem?

+
Learning this theorem is crucial as it forms a foundation for understanding more complex geometric relationships and problem-solving techniques.



