5 Tips for Mastering Translation Rotation Reflection Worksheets

Mastering Translation, Rotation, and Reflection worksheets is an essential skill for students delving into the world of geometry and spatial reasoning. These exercises not only enhance understanding of transformations but also improve problem-solving abilities and visual perception. Here are five effective strategies to excel in these types of worksheets:
1. Understand the Basics of Transformation
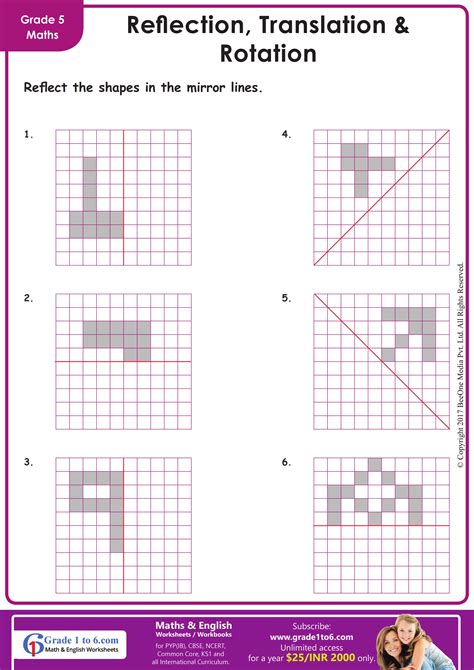
Before you dive into complex transformations, make sure you grasp the fundamentals:
- Translation: Movement of a figure from one location to another without changing its orientation. Use coordinates to calculate the shift.
- Rotation: Spinning a figure around a fixed point, often the origin (0,0). Know the degrees of rotation and how to use positive or negative values to determine the direction of spin.
- Reflection: Creating a mirror image of a shape across a line of symmetry. Visualize how the figure would look on the other side of this line.
💡 Note: Regular practice with coordinate geometry will make you more adept at handling transformations effortlessly.
2. Visualize Each Transformation

Picturing the transformation process in your mind before executing it on paper is crucial:
- Sketch the original figure.
- Imagine performing the transformation step-by-step.
- Verify the result with simple transformations, like translating a square horizontally or vertically.
- Use tools like tracing paper or geometric apps to visualize the transformations if you find it challenging.
🔎 Note: Spatial visualization is a skill that develops with practice and can be significantly improved by engaging with visual puzzles or video games involving rotations.
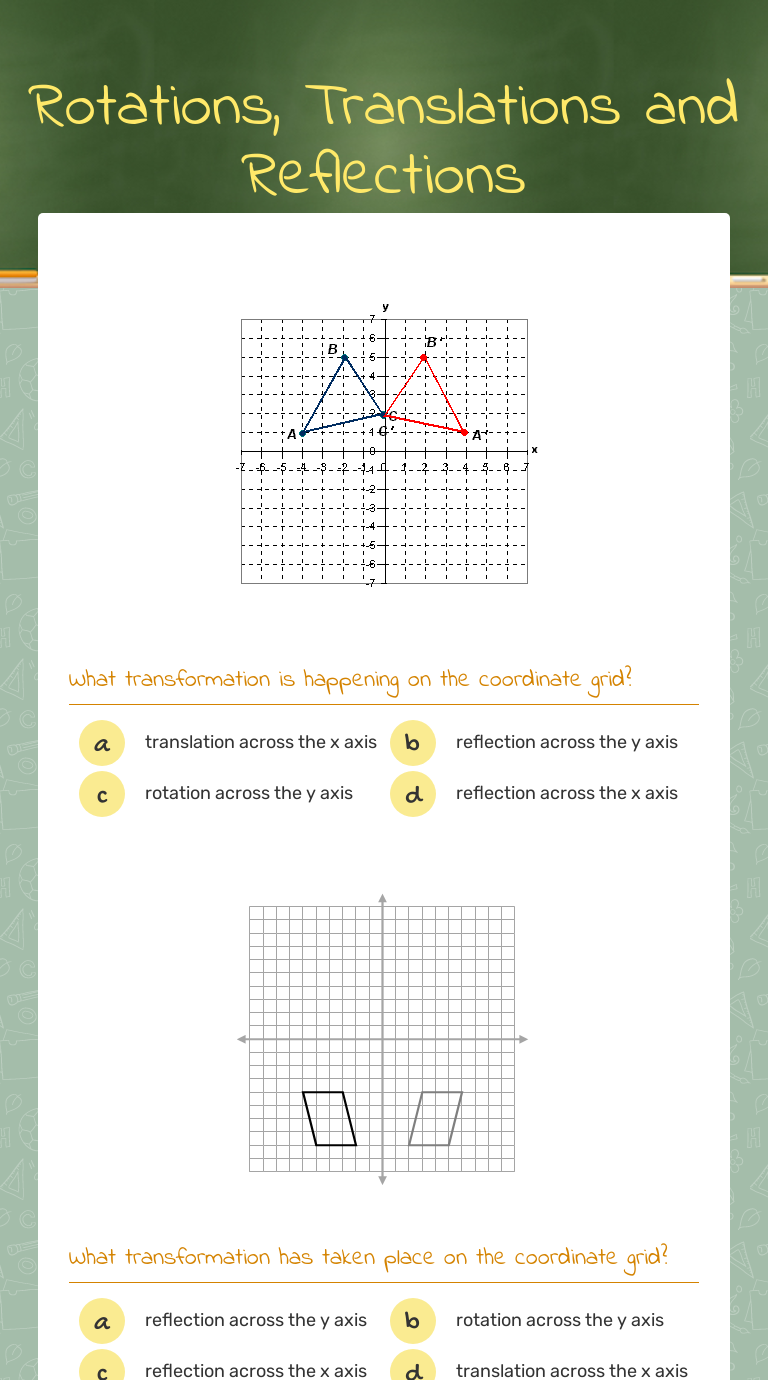
3. Master the Coordinate Grid System

Transformations on a worksheet often occur in a coordinate grid:
- Translation: Shift the coordinates by adding or subtracting values to x and y.
- Rotation: Understand how to change the coordinates based on the angle of rotation (45°, 90°, 180°, etc.).
- Reflection: Flip coordinates relative to the line of reflection. For example, reflect over the x-axis by changing the y-coordinate’s sign.
| Transformation | Coordinate Change |
|---|---|
| Translation | (x+dx, y+dy) |
| Rotation | Complex formulas based on rotation angle |
| Reflection | Change sign of coordinate relative to axis |

🧐 Note: Coordinate systems are not just for academic exercises; they are foundational in fields like computer graphics and animation.
4. Practice with Specific Worksheets

Find and work through dedicated transformation worksheets:
- Look for worksheets with varying complexity.
- Try different shapes, not just basic polygons.
- Focus on both algebraic and geometric methods of transformation.
- Identify patterns in transformations to streamline your thought process.
📌 Note: Websites like Math-Aids offer free, customizable worksheets to practice these skills.
5. Use Mnemonics and Visualization Techniques

Make transformations memorable through mnemonics:
- For rotations, remember ROAR (Rotate, Origin, Axis, Rotation).
- Create simple memory aids like “Turn, Slide, Flip” for Translation, Rotation, and Reflection respectively.
- Visualize the shape transforming in your mind before plotting it on paper to check if your visualization aligns with your calculation.
🧠 Note: Mnemonics can significantly reduce cognitive load when dealing with multiple transformations in a single worksheet.
To excel in Translation, Rotation, and Reflection worksheets, students must combine theoretical knowledge with practical skills. By understanding the basics, visualizing transformations, mastering coordinate systems, practicing with specific worksheets, and using mnemonic devices, you’ll significantly improve your ability to handle these geometric operations with ease and accuracy.
Summarizing these key points, the path to mastering Transformation worksheets involves understanding core concepts, visualization, practical application through coordinate geometry, targeted practice, and clever memory aids. These methods not only prepare you for academic assessments but also enrich your spatial awareness and problem-solving skills in everyday situations.
What if I can’t visualize rotations?

+
Start with simple shapes and rotations around the origin. Physical tools like protractors or dynamic geometry software can also help in visualizing these transformations.
How do I practice transformation if I don’t have worksheets?
+
Use graph paper to manually create your own transformation problems or explore online geometry tools and interactive websites that offer free resources for transformation practice.
Can I use calculators for transformation?

+
Calculators can compute complex coordinate changes, but understanding the principles behind the transformation is essential. Use calculators as a tool to verify your answers, not to replace understanding.