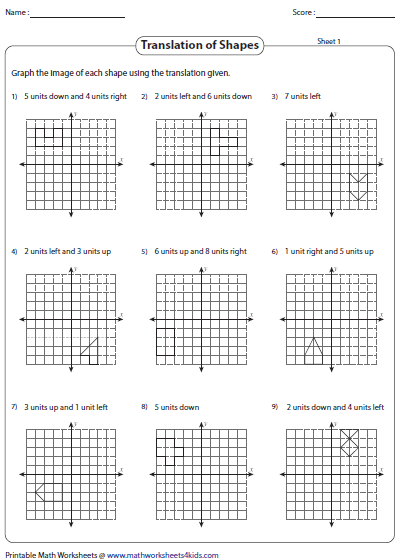
5 Ways to Master Shape Translations in Worksheets
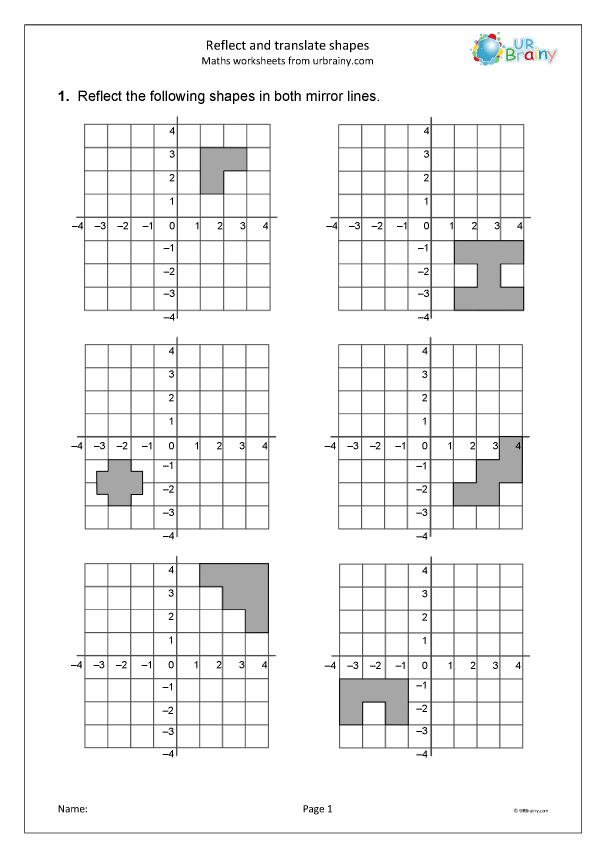
Shape translations in geometry are fundamental concepts that can transform a student's understanding of space, orientation, and movement. Translating shapes on a worksheet is not just an academic exercise; it's a practical tool used in fields ranging from robotics to architectural design. In this comprehensive guide, we will explore five effective strategies to master shape translations, ensuring learners can not only execute these movements accurately but also understand the underlying principles that govern them.
Understanding the Basics of Shape Translation
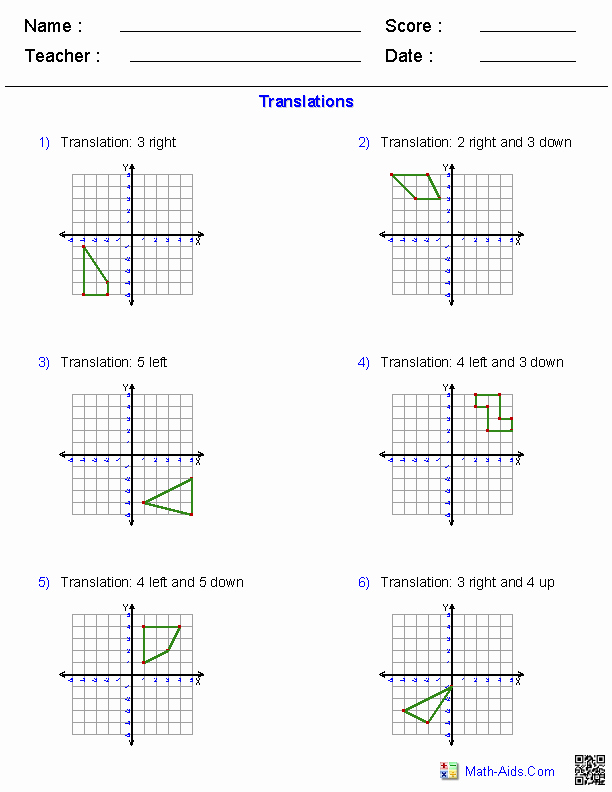
Before delving into the techniques, it’s crucial to grasp what shape translation entails:
- Definition: Translation is a transformation where every point of a shape is moved in the same direction and the same distance. The shape does not change size or orientation.
- Vector: Translation can be described using a vector, which specifies the direction and distance of the move. For example, (2, 3) means moving 2 units to the right and 3 units up.
- Coordinates: Shapes can be translated by altering their coordinate values. If (x, y) are the coordinates of any point on the shape, after translation by vector (a, b), the new coordinates would be (x+a, y+b).
An image depicting translation on a grid can be embedded here to visually aid understanding.
Technique 1: Use of Graph Paper or Grids

Using graph paper or grids is an intuitive approach to visualize and perform shape translations:
- Plot the original shape on the graph paper or grid.
- Identify the translation vector.
- Move each point of the shape along the grid according to the vector, creating a new shape.
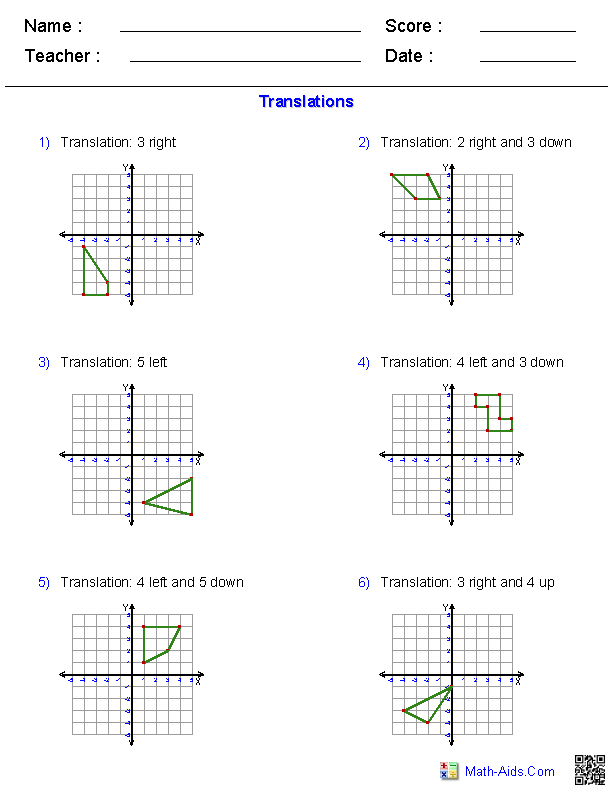
Technique 2: Coordinate Translation

This method involves mathematical calculation to translate shapes:
- List the coordinates of the vertices of the shape.
- Apply the translation vector to each coordinate: new_x = old_x + a, new_y = old_y + b.
- Connect the new coordinates to form the translated shape.
Technique 3: Physical Manipulation

For a kinesthetic learning approach, physical manipulation can be employed:
- Use cutouts of shapes or 3D models.
- Move the shape along a given direction to simulate translation.
- This can be followed by plotting the new position on graph paper for verification.
Technique 4: Software and Apps

With technology at our fingertips, various software and apps can help in understanding translations:
- Interactive geometry software like GeoGebra allows for dynamic shape manipulation.
- Drag-and-drop features simulate translations visually and accurately.
- Online worksheets with embedded sliders can teach translation in an engaging manner.
Technique 5: Algebraic Equations
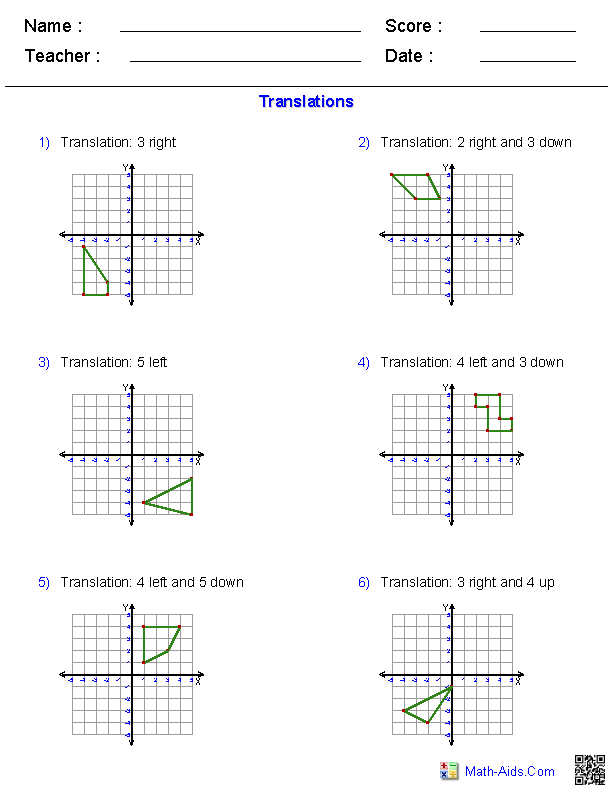
For those who are comfortable with algebra, shape translation can be approached through equations:
- Define the shape using equations or inequalities.
- Translate the shape by changing the constants in these equations.
- Visualize or graph the new shape after the transformation.
👓 Note: Each method has its place in education, depending on the student's learning style and the complexity of the task. Combining visual aids with mathematical operations can provide a comprehensive learning experience.
Engaging with Worksheets

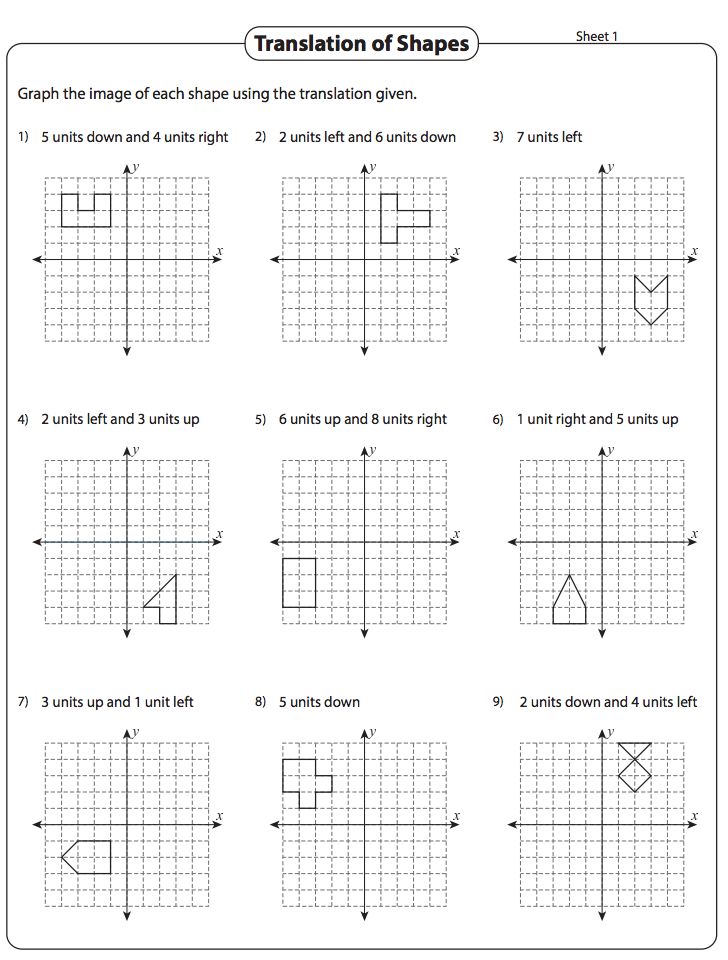
Worksheets play an essential role in mastering shape translation:
- Practice: Regular practice with different shapes and translation vectors reinforces learning.
- Visualization: Worksheets often include diagrams or grids to help visualize the transformation process.
- Problem Solving: They provide puzzles and problems where students must find the translation vector or the new shape’s position.
👓 Note: Worksheets should be designed to gradually increase in difficulty to challenge students as they progress in their understanding of shape translations.
Advancing Beyond Basics

After mastering the fundamental techniques, here are ways to advance your skills:
- Multi-step Translations: Engage with problems where a shape undergoes multiple translations.
- Combining Transformations: Learn how translation interacts with rotation, reflection, and dilation.
- Real-World Applications: Explore how translations are used in real-world scenarios like computer graphics, 3D modeling, and engineering.
In summary, shape translations are a critical aspect of geometry that enhance our ability to manipulate and understand spatial relationships. Through the five techniques detailed above, along with consistent practice on worksheets, learners can develop a robust understanding of translations. Whether you prefer the tactile nature of physical manipulation or the precision of algebraic calculations, there's a method suited to every learning style. Incorporating these strategies into your educational toolkit will not only improve your grasp of this geometric transformation but also spark an interest in the broader applications of mathematics in our daily lives.
What is the difference between translation and rotation?
+
Translation moves a shape without changing its orientation, whereas rotation turns a shape around a fixed point. Translation involves moving every point the same distance in the same direction, while rotation involves every point moving in a circular path.
Can a shape be translated multiple times?
+
Yes, a shape can undergo multiple translations. You can perform each translation sequentially, applying the next translation vector to the result of the previous one.
How does translation affect the area of a shape?
+
The area of a shape remains unchanged after translation, as it simply involves moving the shape without stretching or compressing it.