5 Easy Steps for Translating Coordinates on a Plane

In the realm of mathematics, understanding how to manipulate and interpret coordinate systems is crucial, especially for those involved in fields like graphing, cartography, and computer graphics. Here, we explore how to translate coordinates on a plane, which is a fundamental concept in the transformation of geometric figures. Whether you're a student, an engineer, or a hobbyist in graphics, these steps will guide you through translating points effortlessly.
1. Identifying the Original Coordinates
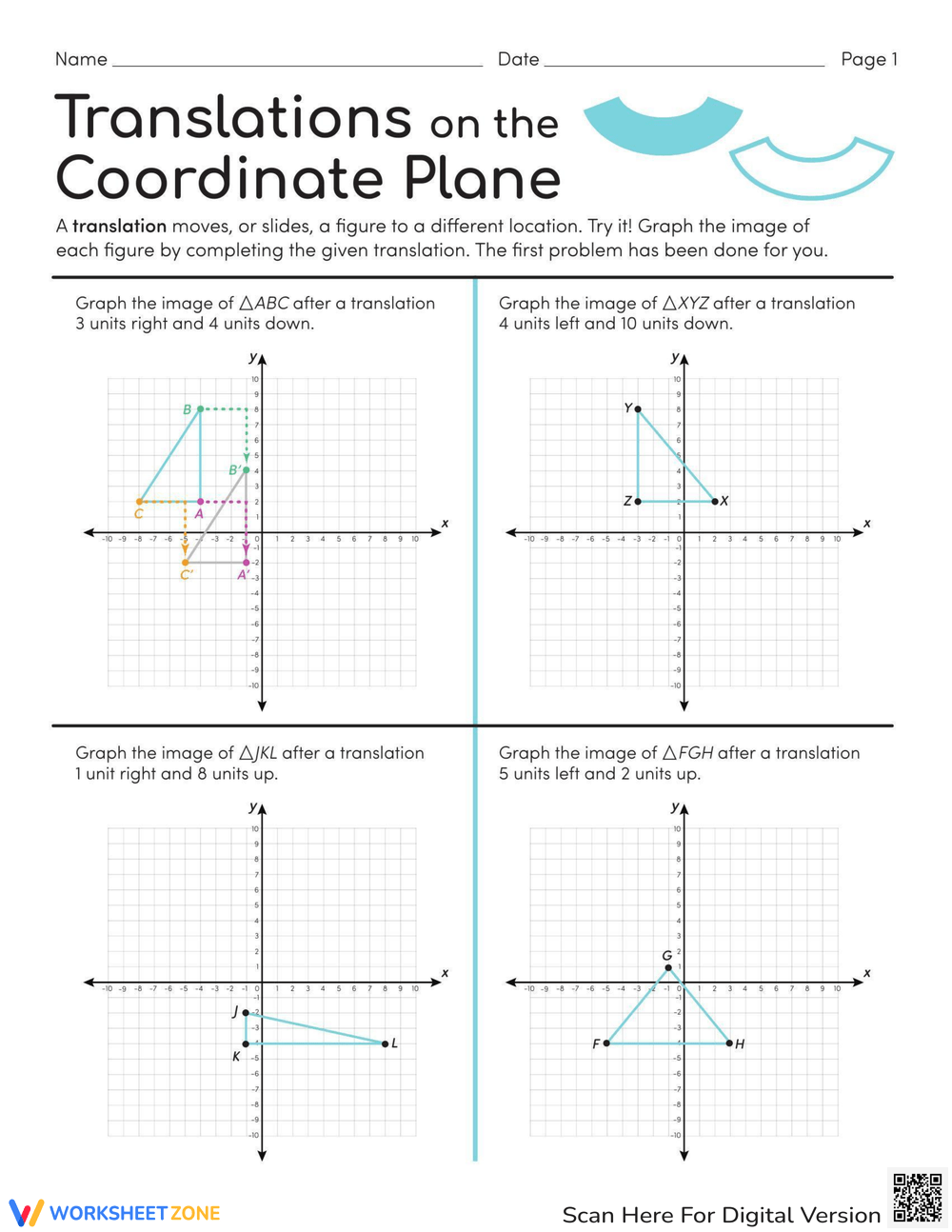
Begin with identifying the coordinates of the points you wish to translate:
- Each point on the plane has a unique pair of coordinates (x, y).
- Ensure you are familiar with the placement of these coordinates within the coordinate system.
2. Determining the Translation Vector

A translation vector describes how much you want to shift the points:
- It consists of two components: a horizontal shift (h) and a vertical shift (k).
- If you’re moving the point to the right, the horizontal component (h) is positive; if left, it’s negative.
- Similarly, for an upward shift, the vertical component (k) is positive, and for downward, it’s negative.
3. Applying the Translation Formula

The formula for translating a point from (x, y) to (x’, y’) is:
- x’ = x + h
- y’ = y + k
📐 Note: This formula assumes your translation vector is [h, k].
4. Plotting the New Coordinates

Once you’ve calculated the new coordinates, plot them on the plane:
- These points will now appear shifted from their original positions.
- Ensure your grid or plane allows for accurate plotting.
5. Verifying the Transformation

Confirm the accuracy of the translation:
- Measure the displacement between original and translated points to ensure it matches the translation vector.
- If possible, use software or tools to visualize and verify the transformation.
Real-World Applications

Understanding coordinate translation has numerous practical uses:
- In navigation systems, it allows for route adjustments.
- In 3D modeling, it’s fundamental for object placement.
- Graphic designers use it to align or reposition elements in their designs.
Conclusion

Mastering coordinate translation not only deepens your understanding of mathematics but also provides practical tools for various applications. By following these steps, you can manipulate points with confidence, ensuring precise transformations in both academic and professional settings.
What is the difference between translation and rotation?

+
Translation involves shifting points in space, while rotation involves turning a figure around a fixed point or axis.
Can I translate coordinates in three-dimensional space?

+
Yes, you can apply similar principles to translate points in 3D space using three translation components for each axis.
How do I know if I’ve translated correctly?

+
Check the distance between the original and new coordinates; it should equal the translation vector. Visualization tools can also help confirm the transformation.