5 Tips for Solving Algebra 1 Linear Functions

In the mathematical journey of algebra, understanding linear functions is not just a step but a leap toward grasping the core concepts that form the foundation of advanced mathematics. Linear functions are the simplest and most prevalent type of function, making them an essential part of the algebra curriculum. Here, we will explore five pivotal tips that can transform your approach to solving linear functions in Algebra 1, ensuring you not only learn but also retain this valuable knowledge effectively.
1. Understand the Basic Components of Linear Functions


The first step in mastering linear functions is to understand their core components:
- The Slope (m): The slope of a line measures its steepness. It indicates how much the dependent variable (y) changes for each change in the independent variable (x). The slope is represented by the formula ( m = \frac{\Delta y}{\Delta x} ).
- The Y-intercept (b): This is the point where the line intersects the y-axis. It tells you where your line starts before any change in x occurs. The y-intercept is typically noted as b in the equation ( y = mx + b ).
To become adept at linear functions:
- Memorize the slope-intercept form of a line: y = mx + b .
- Learn to identify and interpret what each part of the equation means in real-world terms.
💡 Note: Linear functions are also known as first-degree polynomials, where the highest power of the variable x is one.
2. Utilize Graphing Tools
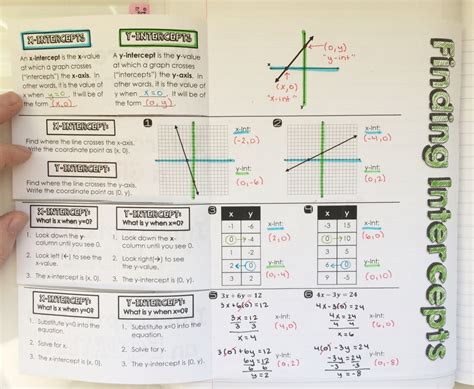

Graphing linear functions visually helps in understanding their behavior:
- Plot Points: Start by plotting the y-intercept, then use the slope to find another point. Connect these with a straight line.
- Use Graphing Calculators or Software: Modern tools can provide a visual representation of linear functions, allowing for quick checks on your work and deeper insight into how changing m and b affects the line.
- Interactive Tools: Websites and apps that offer interactive graphing are invaluable for learning how slopes and y-intercepts work together to shape the function.
3. Practice with Slope Intercept Equations

Here’s how you can sharpen your skills with linear equations:
- Transform Equations: Get into the habit of converting equations into slope-intercept form. It simplifies solving and understanding.
- Work with Different Forms: Beyond the slope-intercept form, familiarize yourself with other forms like the point-slope form (y - y1 = m(x - x1)) and the standard form (Ax + By = C). Each form has its use.
- Apply Linear Functions: Engage in real-life word problems where linear functions describe a situation, like predicting sales growth or tracking the progression of distance over time.
💡 Note: The slope-intercept form provides immediate information on the slope and y-intercept, making it particularly handy for interpreting linear functions in practical scenarios.
4. Use Tables to Organize Data


When dealing with linear functions:
- Create a table of values that show how x and y relate:
| x | y |
|---|---|
| 0 | b |
| 1 | m + b |
| 2 | 2m + b |

- Recognize patterns, especially how the y values change with each step in x. This table can help you to plot points on a graph.
- Understand how these values can be used to calculate the slope (the rate of change) and the y-intercept.
5. Reflect on the Real-World Applications

Here are some practical applications of linear functions:
- Economics: Revenue and Cost functions are linear, where the slope represents the rate of change.
- Physics: The motion of an object under constant acceleration can be described by a linear equation where velocity is the slope and initial displacement is the y-intercept.
- Engineering: Linear functions help in design and analysis, for instance, determining the stress on a beam under load.
By reflecting on these real-world applications, you not only understand why linear functions are useful but also improve your conceptual grasp through their practical significance.
These tips, if applied diligently, will not only aid you in solving linear function problems but will also deepen your understanding of algebra. The key is practice and recognizing the underlying patterns in linear functions. From calculating slopes to interpreting graphs, each aspect of linear functions provides a foundation for more complex topics in mathematics. Whether you’re analyzing data, solving real-world problems, or just enhancing your problem-solving skills, mastering linear functions is an essential step on your mathematical journey. To achieve proficiency:
- Spend time regularly practicing different types of problems.
- Engage with visual aids like graphs and tables for better conceptual understanding.
- Link theoretical knowledge to practical applications for a fuller grasp of the subject.
What are some common mistakes students make when solving linear functions?

+
Students often forget to isolate the y-variable when solving for the slope-intercept form. They might also confuse the signs when calculating slopes or incorrectly interpret the y-intercept as the slope.
How can I quickly identify the slope from a linear equation?

+
Identify the coefficient of x in the equation ( y = mx + b ). If the equation is not in slope-intercept form, rearrange it to isolate y, and then the coefficient of x will be your slope (m).
Why is it important to graph linear functions?

+
Graphing allows you to visualize the relationship between variables, understand the behavior of the function, and check for accuracy in calculations. It also helps in interpreting the function’s slope and y-intercept in a practical context.


