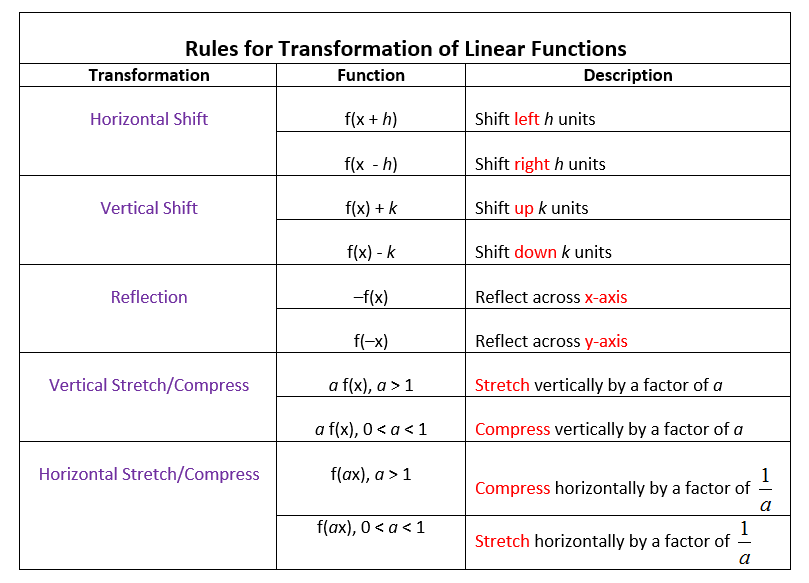
Transforming Linear Functions Worksheet: Master Your Skills

Understanding linear functions is essential for any student in algebra, as they form the foundation for understanding more complex mathematical concepts. Whether you're a high school student aiming to grasp the basics or someone revisiting algebra, this comprehensive guide will help you master your skills with linear functions through a detailed worksheet designed to enhance your understanding.
Why Linear Functions?

Linear functions are crucial in mathematics because:
- They are easy to visualize through straight lines.
- They are used in various real-world applications like economic modeling, physics, and engineering.
- They serve as a building block for understanding calculus.
Components of a Linear Function

Before diving into the worksheet, let’s review what a linear function looks like:
- A linear function can be written in the form y = mx + b, where:
- m represents the slope or gradient, which dictates the steepness of the line.
- b represents the y-intercept, where the line crosses the y-axis.
Worksheet Overview

Here’s a structured worksheet to help you practice:
| Question | Type | Example |
|---|---|---|
| Determine the slope | Application | Find the slope of the line passing through (3,5) and (6,7). |
| Write the equation | Practice | Find the equation of the line with a slope of 2 and passing through point (1,3). |
| Graph the line | Visual | Graph y = 2x - 3. |

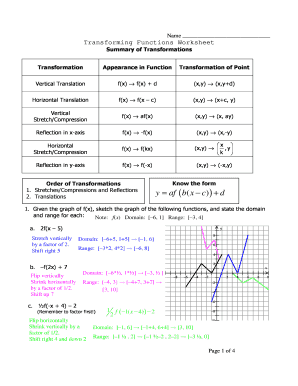
Step-by-Step Solutions

To help you grasp the material thoroughly, let’s delve into how to approach each type of problem:
Determining the Slope

The slope can be calculated using the formula:
- m = (y2 - y1) / (x2 - x1)
For the example given in the worksheet:
- Slope for the line passing through (3,5) and (6,7) would be m = (7 - 5) / (6 - 3) = 2 / 3.
Writing the Equation

Given the slope and a point, you can use the point-slope form of the line equation:
- y - y1 = m(x - x1)
Let’s work through the example:
- For a slope of 2 passing through (1,3), the equation would be y - 3 = 2(x - 1), which simplifies to y = 2x + 1.
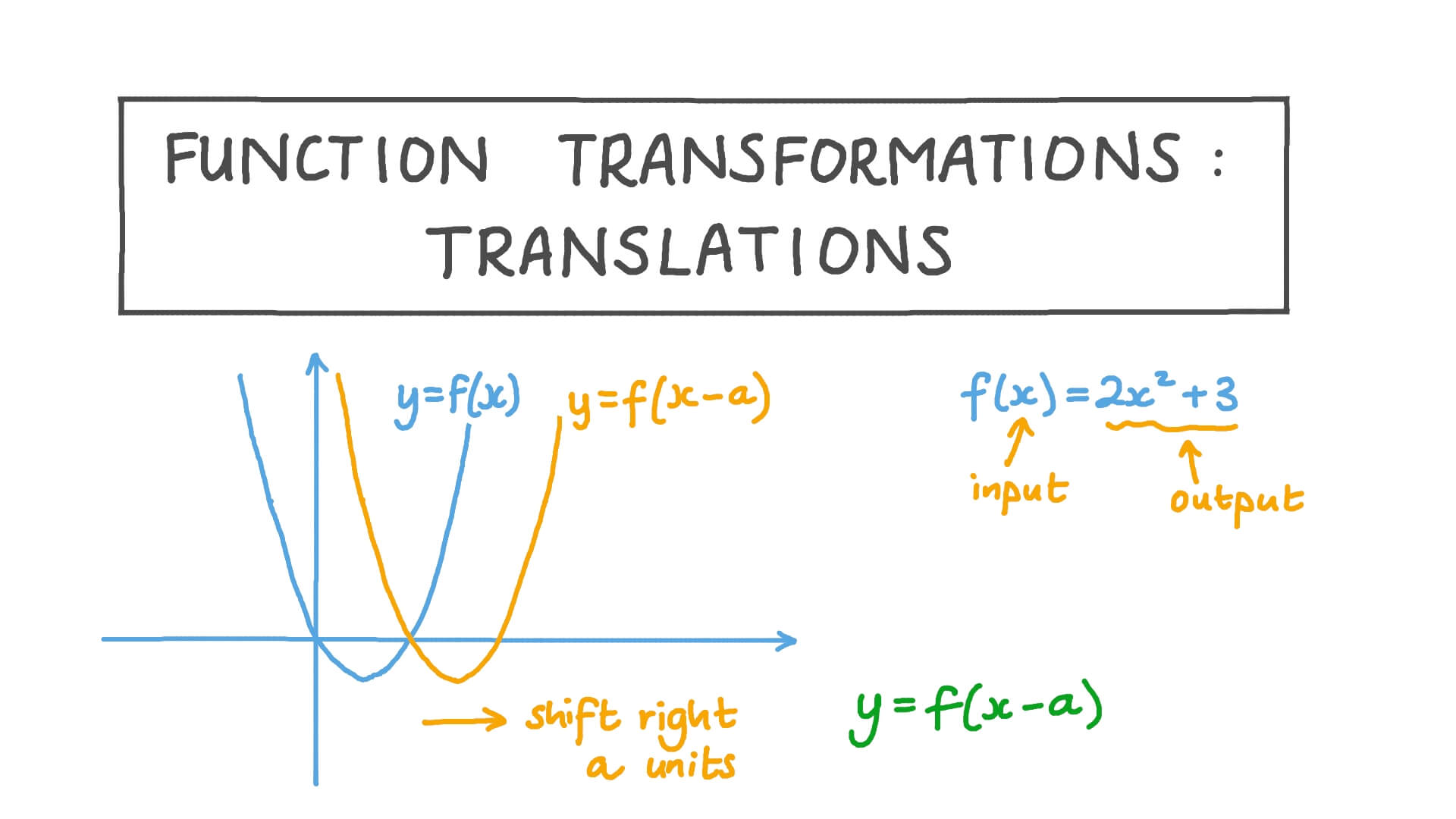
Graphing the Line
Graphing involves plotting points and connecting them:
- For y = 2x - 3, you might choose points like (0, -3), (1, -1), and (2, 1) to plot and then draw the line through these points.
📝 Note: Remember to always label your axes when graphing.
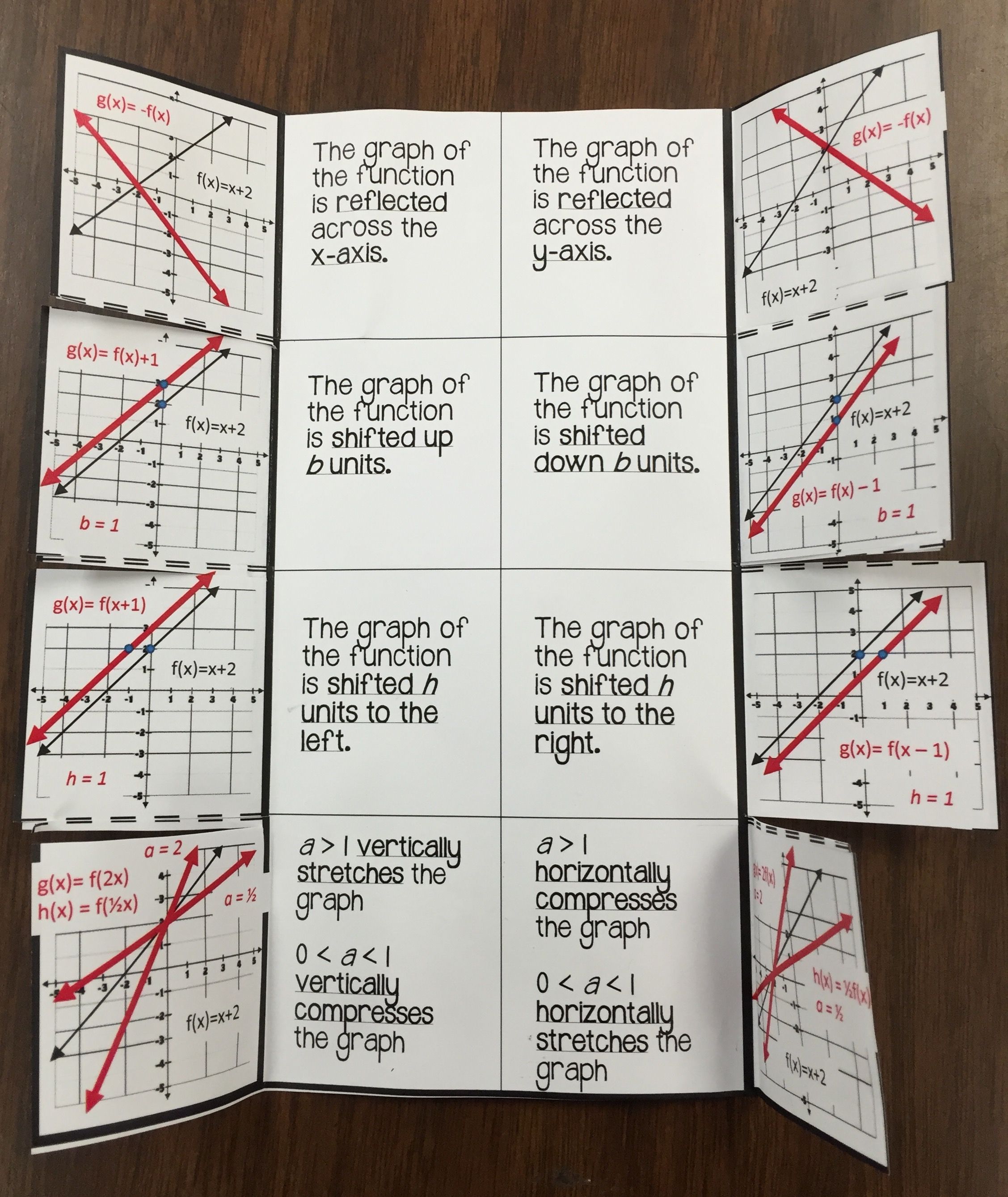
Practice Problems

Now it’s your turn to test your understanding. Here are some practice problems:
- Find the slope of the line through (-2,4) and (3,-1).
- Write the equation of the line with slope -1 passing through (5,8).
- Graph the line y = -1/2x + 5.
To solidify your understanding, tackle these problems:
In Conclusion
Moving forward with linear functions, you’ll find that the principles you’ve mastered here will serve as a cornerstone for more intricate mathematical problems. Understanding slope, how to write equations of lines, and how to graph them are pivotal not just in algebra but in various scientific and practical applications. Keep practicing, exploring real-world scenarios, and don’t shy away from asking questions or seeking deeper understanding. Your ability to manipulate and comprehend linear functions is a stepping stone to mastering advanced mathematical concepts.
What is the importance of slope in a linear function?
+
The slope in a linear function tells you how much the y-value changes for every unit increase in x, essentially representing the rate of change or the “steepness” of the line.
Can a linear function have a negative slope?
+
Yes, a linear function can have a negative slope, which means the line is decreasing as x increases.
How does the y-intercept affect the graph of a linear function?

+
The y-intercept affects where the line crosses the y-axis. A positive intercept moves the line upward, and a negative one moves it downward.