5 Transformations of Functions Worksheet Tips for Students

Welcome to the exciting world of function transformations, where understanding how to modify and manipulate mathematical functions can open doors to complex problem-solving and visualization in various fields of study. Whether you're a high school student wrestling with algebra or a college student preparing for an advanced math course, mastering transformations is key to excelling in mathematics. Here are five tips to help you navigate through the world of function transformations:
The Basics of Transformation

Before diving into the specifics, ensure you understand the fundamental types of transformations:
- Translation: Moves the function horizontally or vertically without changing its shape.
- Reflection: Mirrors the function across an axis or a line.
- Scaling: Expands or compresses the function, changing its size or direction of increase/decrease.
- Rotation: Rotates the function around a point, typically the origin.
- Dilation: A special case of scaling where the function is stretched or compressed away from the origin.
📝 Note: For complex functions, these transformations can interact, producing a combined effect.
Understand the Impact of Parameters

Each transformation involves parameters that affect how the function changes:
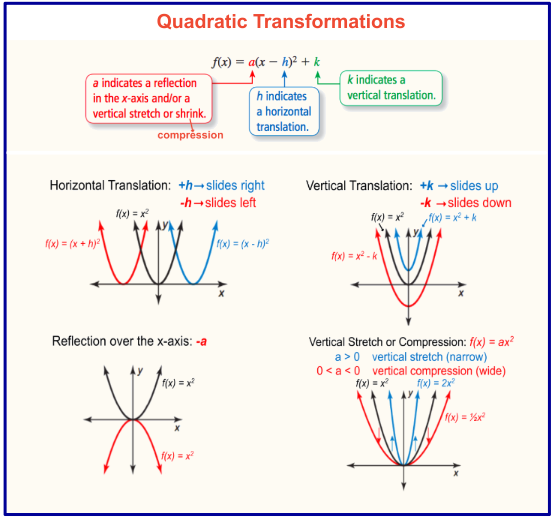
- c in f(x + c) represents a horizontal shift; if c is positive, the function moves to the left, and if negative, to the right.
- c in f(x) + c indicates a vertical shift; positive c shifts the graph up, negative shifts it down.
- Multiplication by a before or after f(x) affects the vertical or horizontal scaling. For example, a * f(x) vertically scales by a factor of a.
Visualize these changes by imagining how the graph would transform when you alter these parameters. This mental exercise can be particularly useful when solving problems involving transformations.
Visualize with Graphing

Graphing is an excellent tool to understand and predict the transformation:
- Parent Functions: Begin with the parent function (e.g., y = x^2 for a quadratic). Understand how transformations will alter this basic shape.
- Transformation Steps: Follow the steps of transformation methodically. For example, if you see f(x - 2) + 3, translate the function 2 units right and then 3 units up.
- Use Graphing Calculators: These tools are invaluable for quick visualization, especially when dealing with multiple transformations at once.
Graphing not only helps in problem-solving but also in reinforcing the conceptual understanding of function behavior.
Practice with Variety

Variation in problems helps solidify your understanding:
- Simple Functions: Start with basic functions like linear, quadratic, and exponential transformations.
- Complex Functions: Move on to trigonometric, rational, and logarithmic functions.
- Combination of Transformations: Combine multiple transformations in one problem to understand how they interact.
Here's a simple table to illustrate common transformations and their effects:
| Transformation | Equation | Effect on Graph |
|---|---|---|
| Vertical Translation | f(x) + k | Up if k > 0, down if k < 0 |
| Horizontal Translation | f(x + h) | Left if h > 0, right if h < 0 |
| Vertical Reflection | -f(x) | Reflected over x-axis |
| Horizontal Reflection | f(-x) | Reflected over y-axis |

Link to Algebra and Geometry
Understanding transformations goes beyond pure algebra; it's also integral to geometry:
- Geometric Interpretations: Translate, reflect, scale, and rotate geometric shapes to understand transformations.
- Vector Transformations: Use vectors to represent and understand translations, rotations, and scaling in two-dimensional space.
- Applications in Real-Life: Consider how transformations can be applied in real-world problems, such as computer graphics, engineering design, or even simple tasks like resizing images.
🚨 Note: Geometric transformations can often help students visualize algebraic manipulations better.
Now that we've covered these five key tips for understanding transformations of functions, let's tie it all together. The ability to transform functions not only aids in solving problems but also helps in visualizing and understanding the dynamic nature of mathematical functions. As you continue your studies, remember that transformations are not just tools for shifting graphs but are fundamental to understanding how mathematical objects behave. This knowledge will serve you well across various mathematical disciplines, enhancing your analytical skills and providing a deeper insight into how things change, move, and interact within mathematical systems.
What is the difference between horizontal and vertical translations?

+
Horizontal translation changes the input value by shifting the graph left or right. For example, f(x + 3) shifts the graph to the left by 3 units. Vertical translation, on the other hand, changes the output value by moving the graph up or down. An example would be f(x) + 2, which shifts the graph up by 2 units.
Can transformations be applied to any function?

+
Yes, transformations can be applied to any function, whether it’s linear, quadratic, trigonometric, or otherwise. However, the effect of the transformation on the function’s shape and behavior can vary significantly based on the nature of the function.
Why is visualization important in function transformations?

+
Visualization helps students conceptualize how transformations alter the shape and position of a function’s graph. It makes abstract algebraic operations tangible, facilitating a deeper understanding of how changes in parameters affect the function’s behavior.



