5 Essential Transformations of Functions Practice Tips

Practice makes perfect, especially when you're mastering the transformation of functions in mathematics. Here, we will guide you through the process of understanding how functions can be manipulated through various transformations, including translations, reflections, stretches, and shrinks. These transformations are not just the fundamentals of algebra but crucial for further study in calculus, physics, and engineering. Let's delve into the essential tips to ensure your learning is both effective and enjoyable.
Understanding Basic Transformations

Before we get into more complex transformations, let's clarify the four basic ways functions are transformed:
- Translations: Moving a function horizontally or vertically.
- Reflections: Reflecting a function over an axis or line.
- Stretches and Shrinks: Stretching or shrinking a function in specific directions.
- Rotations: Rotating a function around a point or an axis.
These transformations can significantly alter the appearance and behavior of a function, making understanding their principles key to mastering graphical representations.
Tip 1: Visualize the Transformations

Visualization is a powerful tool in mathematics, and it's particularly helpful when dealing with function transformations. Here's how you can make the most of visual aids:
- Use graphing tools or software like Desmos or GeoGebra to visually manipulate functions.
- Sketch transformations step-by-step. For example, if you're translating the function f(x), start with the original graph, then move the function to the left or right to understand what shifting does to the function.
- Create cheat sheets with before-and-after diagrams for each type of transformation to compare visually.
🌟 Note: Visualizing transformations helps cement the abstract concepts into concrete understanding, enhancing your ability to recall and apply these principles in more complex scenarios.

Tip 2: Master the Function Notation
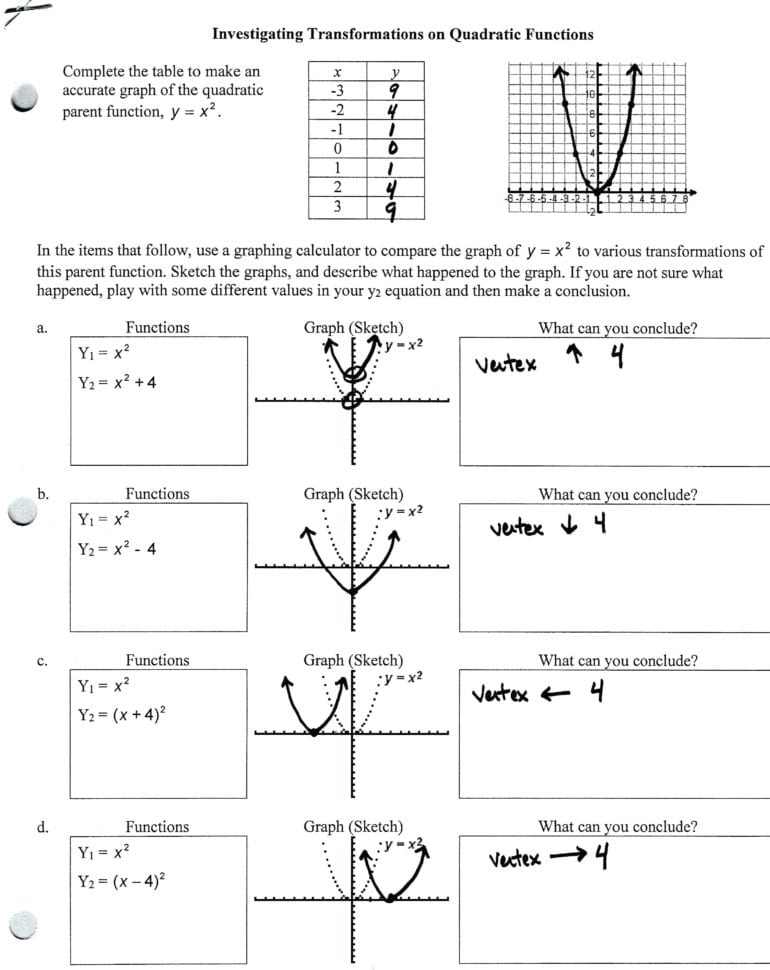
Understanding the notation is vital. Here’s what to know:
| Transformation | Function Notation | Effect on Graph |
|---|---|---|
| Vertical Translation | f(x) + c | Shifts the graph up by c units |
| Horizontal Translation | f(x - c) | Shifts the graph to the right by c units |
| Vertical Stretch/Compression | a*f(x) | Stretches if |a|>1, compresses if |a|<1 |
| Reflection over x-axis | -f(x) | Mirrors the graph over the x-axis |

This table can serve as a quick reference. Practice identifying these transformations in function notations to enhance your proficiency.
Tip 3: Practice with Specific Functions

Applying transformations to different types of functions solidifies your grasp:
- Linear Functions: Practice translating and reflecting lines. For example, how would y = 2x + 1 change if translated horizontally?
- Quadratic Functions: Focus on vertical and horizontal shifts, reflections, and stretches.
- Trigonometric Functions: Understand how translations affect periodicity, amplitude, and the phase shift.
Regularly work through problems where you're required to sketch the original and transformed functions side by side.
Tip 4: Combine Transformations

Real-world applications often involve multiple transformations:
- Start with one transformation at a time. For instance, if you need to translate and stretch a function, do the stretch first, then the translation.
- When combining transformations, ensure you follow the correct order to prevent errors.
- Use examples and exercises where you can combine transformations like reflection, vertical stretch, and horizontal translation in a single problem.
🔍 Note: Understanding the order of operations in transformations is critical as it can significantly change the final shape and position of the function.
Tip 5: Application in Real-Life Problems

Connecting math to real-life scenarios helps:
- Modeling motion problems in physics where transformations can represent changes in velocity, acceleration, or position over time.
- Graphic design and animation where function transformations can create smooth transitions or effects.
- Economics where transformations might model shifts in supply and demand curves.
Look for scenarios where you can apply your understanding of transformations, making your learning more practical and memorable.
In wrapping up, mastering function transformations is not just about understanding algebraic formulas but also about gaining the ability to visualize and manipulate functions in practical scenarios. By consistently practicing these techniques through sketching, notation, specific function practice, combination of transformations, and real-life applications, you'll enhance both your conceptual understanding and your problem-solving skills in mathematics. Remember, the key to mastering any area in mathematics is not just learning the theory but engaging with it through application and continuous practice.
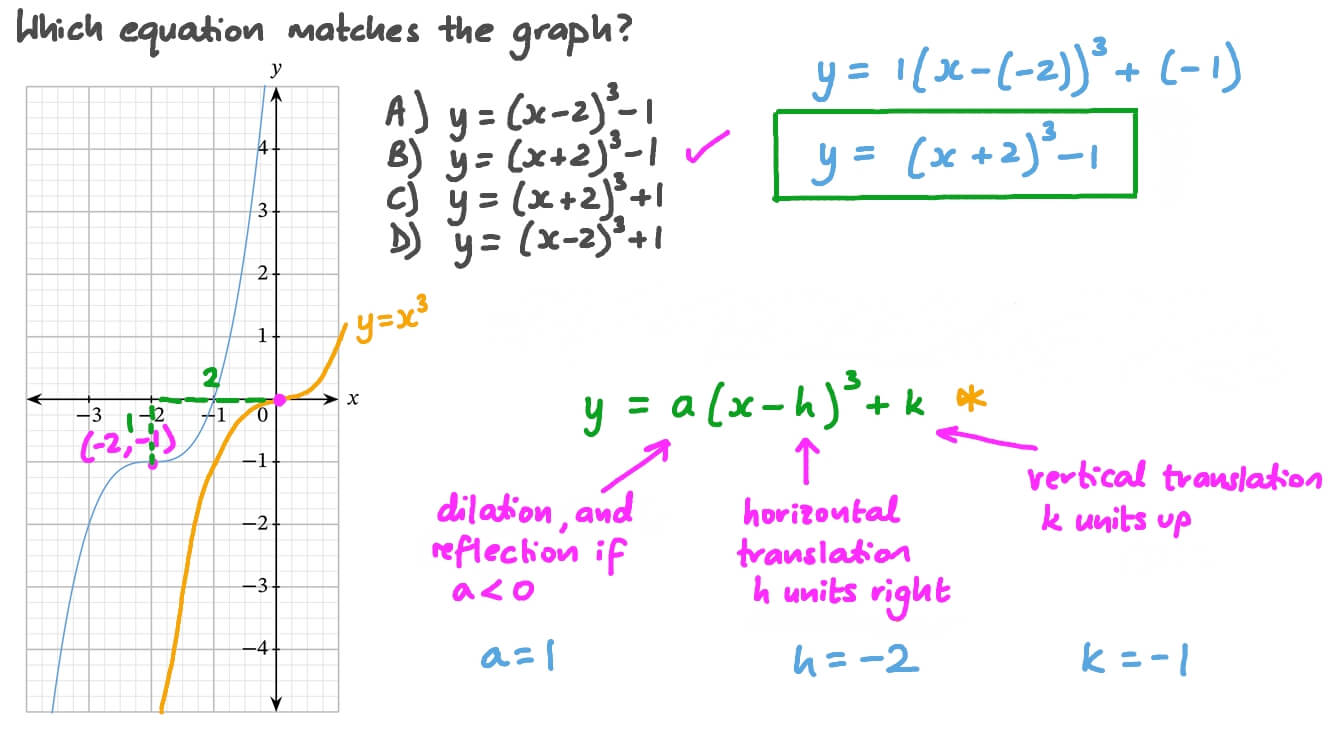
What are the key function transformations?
+
The four basic function transformations are translations, reflections, stretches and shrinks, and rotations. These manipulate a function’s position, symmetry, scale, and angle respectively.
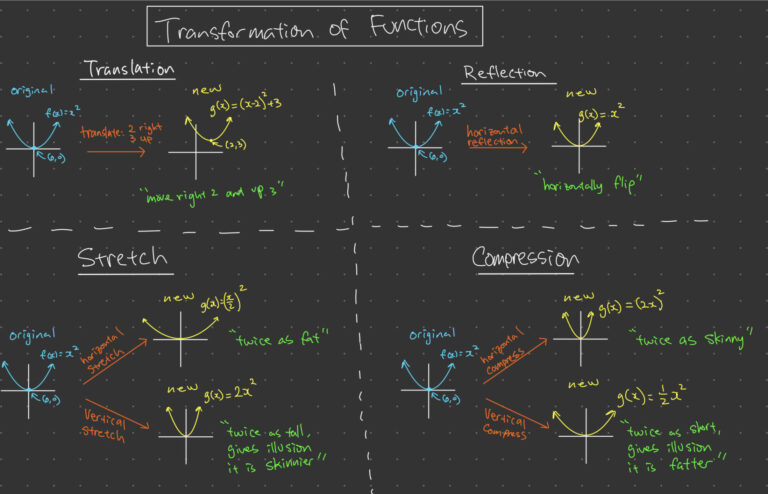
Why are visualizations important in learning function transformations?
+
Visualizations help transform abstract mathematical concepts into tangible, visual representations, which aids in understanding, retention, and application of these concepts.
How can function transformations be applied in real-life?

+
Function transformations are used in physics to model motion, in graphic design for animations, in economics for market analysis, and many other fields where mathematical models can describe changes in variables or systems.