5 Must-Know Linear Function Transformations for Students

Linear functions are fundamental in mathematics, physics, engineering, and many other fields. Understanding their transformations can unlock a myriad of problem-solving techniques and intuitive insights into the behavior of lines in two-dimensional space. Here are five essential transformations of linear functions every student should know:
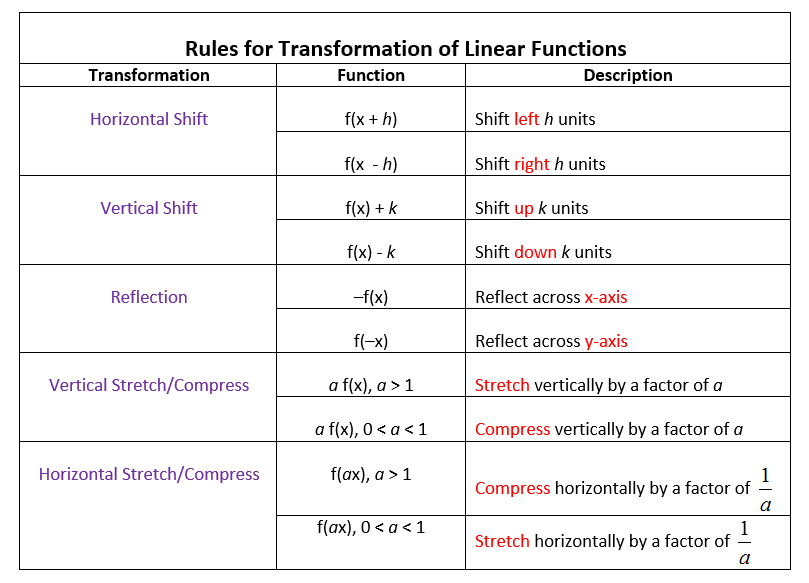
1. Vertical Shift


Shifting a linear function up or down is known as a vertical shift. The function y = mx + b can be transformed to y = mx + b + c. Here, the parameter c dictates the vertical shift:
- Add c to shift the graph c units upwards.
- Subtract c to shift the graph c units downwards.
📚 Note: Remember that the slope m remains unchanged, affecting only the y-intercept b.
2. Horizontal Shift


A horizontal shift involves moving the graph left or right. The function y = mx + b is modified to y = mx + b - dc where c is a horizontal shift:
- Add c to shift the graph c units to the left.
- Subtract c to shift the graph c units to the right.
3. Dilation


Dilation, or scaling, changes the steepness of the line. For a function y = mx + b, dilating vertically involves altering the slope m to a(mx + b) where a is the dilation factor:
- If a > 1, the line becomes steeper.
- If 0 < a < 1, the line flattens.
- If a < 0, the line reflects across the x-axis and becomes steeper or flatter.
📝 Note: Horizontal dilation can also be applied using y = m(x/b) + c, where b affects how the line stretches or compresses horizontally.
4. Reflection


Reflecting a linear function can occur across the x-axis or the y-axis:
- For reflection across the x-axis: change y = mx + b to y = -mx + b.
- For reflection across the y-axis: change y = mx + b to y = m(-x) + b.
💡 Note: Both reflections change the sign of either the x or y terms or both, resulting in a mirror image of the original line.
5. Combinations of Transformations

In real-world applications, linear functions often undergo multiple transformations at once. Consider the function y = 3(x - 2) + 4:
- Vertical shift of 4 units up (from b = 4).
- Horizontal shift of 2 units to the right (from (x - 2)).
- Dilation by a factor of 3 (from 3(x - 2)).
These combined transformations can be applied sequentially or as a single function transformation. The order does not change the final result for linear functions:
- Horizontal shifts applied before or after dilation have the same effect due to the linearity of the transformations.
Understanding these transformations equips students with the tools to model and analyze linear systems effectively. By mastering these fundamental concepts, students can visualize and predict how changes in parameters affect the behavior of linear equations. This knowledge not only aids in solving mathematical problems but also in understanding real-world phenomena where linear relationships are prevalent.
What is the difference between vertical and horizontal shifts?

+
Vertical shifts move the entire graph of a function up or down while keeping its shape the same. Horizontal shifts move the graph left or right, affecting when the function intercepts the x-axis.
How does dilation change a linear function?

+
Dilation or scaling changes the steepness of a linear function, making it either steeper (if the dilation factor is greater than 1) or flatter (if less than 1).
Why are reflections important in understanding linear functions?

+
Reflections help students understand the symmetry and properties of linear functions, providing insights into how lines behave when mirrored across axes or when dealing with inverse functions.
Can transformations be applied in any order?

+
For linear functions, transformations like shifting, dilating, or reflecting can be applied in any order without affecting the final outcome.