Triangle Inequality Theorem Explained: Free Worksheet Inside

The Triangle Inequality Theorem and Its Importance in Geometry
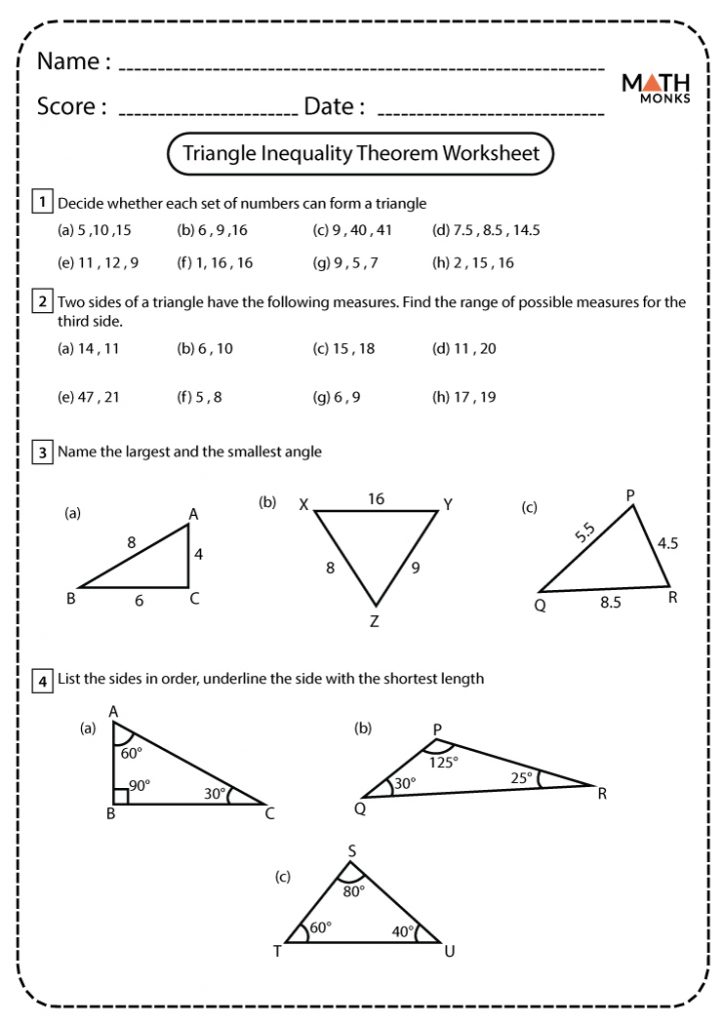
In the fascinating world of geometry, the Triangle Inequality Theorem stands as a cornerstone principle that is both intuitive and fundamental. Whether you’re a math enthusiast, student, or professional in the field, understanding this theorem can provide a clearer grasp of spatial relationships and geometric structures.
Understanding the Triangle Inequality Theorem

At its core, the Triangle Inequality Theorem states:
- For any triangle, the sum of the lengths of any two sides must be greater than the length of the remaining side.
This theorem can be mathematically expressed as:
- a + b > c
- a + c > b
- b + c > a
Where a, b, and c are the lengths of the sides of the triangle. This principle ensures that any three given lengths can form a valid triangle.
Visualizing the Theorem


The Straight Line Distance

To understand why this theorem must hold true, consider the fact that the shortest distance between any two points is a straight line. If the sum of two sides of a triangle was less than or equal to the third side, then one of the angles would need to be 180 degrees or more, which would no longer define a triangle but rather a straight line or a degenerate case of a triangle.
Constructing Triangles

When attempting to construct a triangle with a compass and straightedge, you must adhere to the Triangle Inequality Theorem:
- Begin with any two lengths, say a and b.
- The third side c must lie within the range of |a - b| < c < a + b for the triangle to be constructible.
Practical Applications of the Triangle Inequality
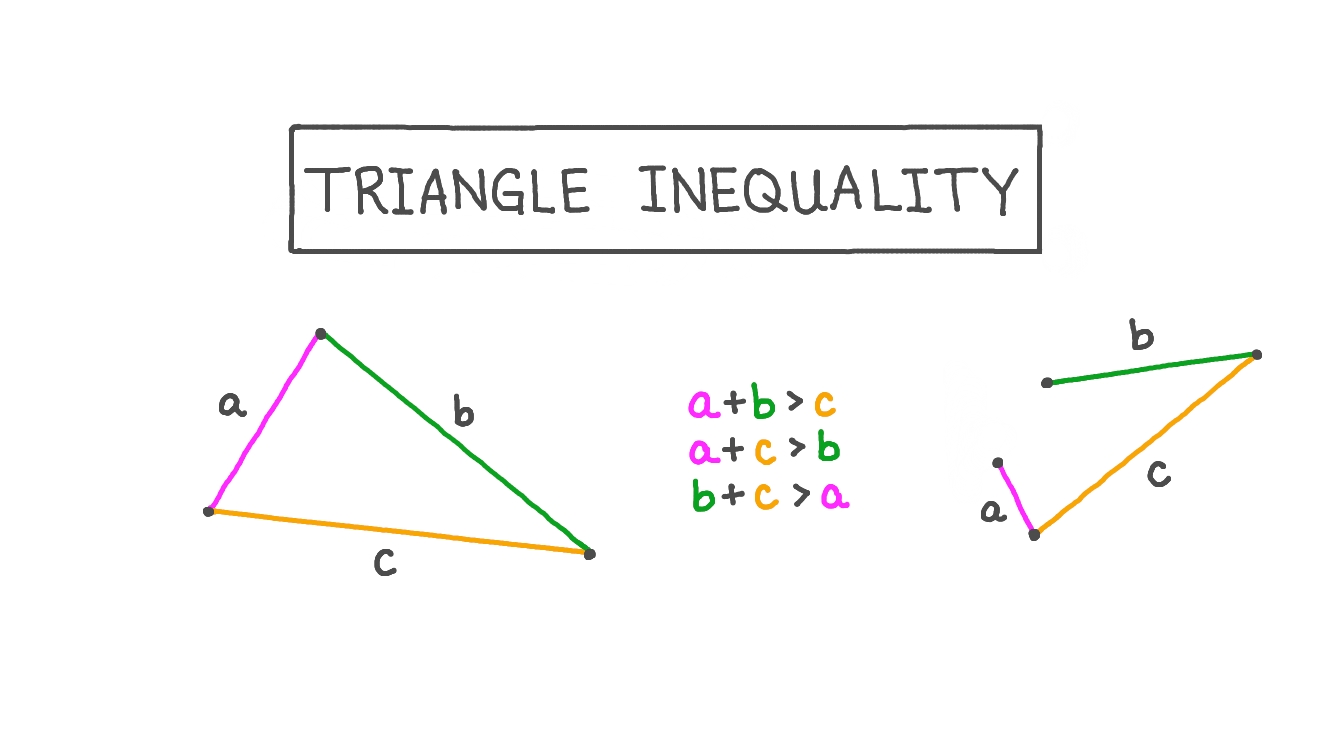
Geometry and Design

This theorem is not merely an academic exercise but has practical applications:
- Architectural Design: Ensuring stability in structures by preventing buckling or collapsing under load.
- Transportation and Navigation: Determining the shortest paths or optimal routes in GPS systems or map applications.
Engineering

The theorem is applied in:
- Structural analysis to ensure that beams or trusses do not violate the triangle inequality.
- Calculating forces in triangular trusses or frames where forces act in a certain direction.
Computer Graphics
In computer graphics, the Triangle Inequality Theorem:
- Helps in optimizing rendering algorithms by checking if triangles are valid before they are drawn.
- Allows for collision detection in video games and simulations, ensuring realistic interactions between objects.
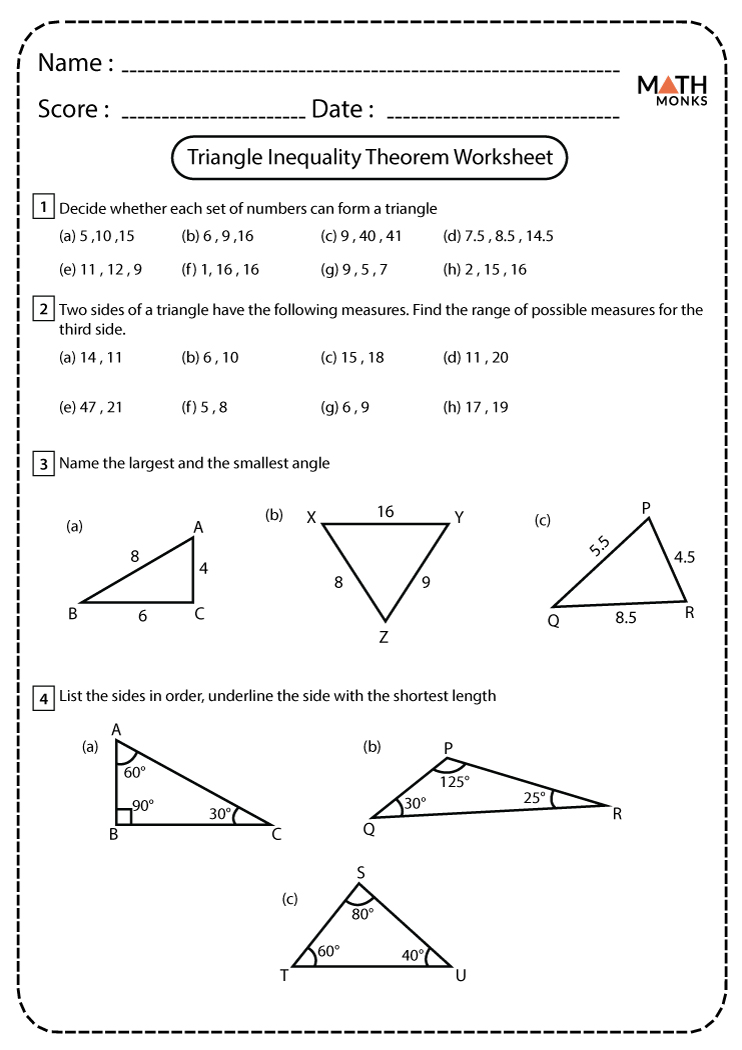
The Theorem in Action: A Worksheet

Here’s an interactive worksheet to explore the Triangle Inequality Theorem:
| Sides of Triangle | Condition 1 | Condition 2 | Condition 3 | Can Form Triangle? |
|---|---|---|---|---|
| a = 3, b = 4, c = 5 | True | True | True | Yes |
| a = 5, b = 5, c = 10 | False | False | False | No |
| a = 7, b = 8, c = 14 | False | False | True | No |

🌟 Note: Always double-check your calculations, as small errors can lead to incorrect conclusions.
The Triangle Inequality Theorem may seem straightforward, but it has profound implications for how we understand geometric shapes and their properties. It's a testament to the elegant simplicity and logic underlying even the most basic mathematical concepts. This principle not only enriches our understanding of triangles but also influences countless practical applications, reminding us how interconnected mathematics is with the world around us.
Can the Triangle Inequality Theorem be applied to any polygon?
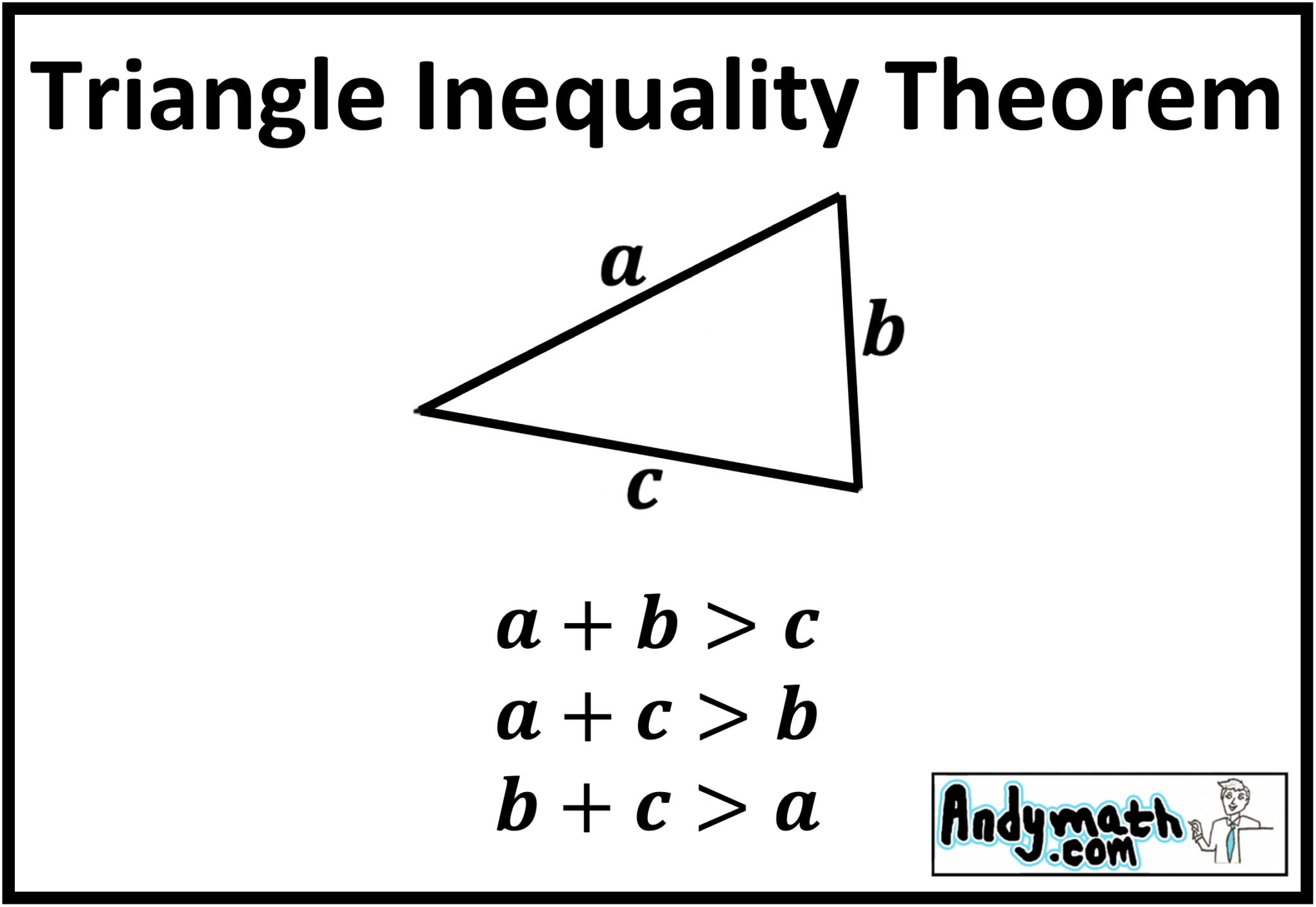
+
While it’s formulated for triangles, the principles behind the Triangle Inequality can be extended to other polygons. For example, the sum of the lengths of any sides must be greater than any one side in a quadrilateral.
What happens if one of the conditions of the theorem is not met?

+
If one or more of the conditions is not met, then the given lengths cannot form a valid triangle. Instead, it might represent a line segment or a degenerate case where the triangle collapses to a straight line or a single point.
How can I remember the Triangle Inequality Theorem?

+
Consider it as a “no straight line” rule for triangles. If any side is as long or longer than the sum of the other two sides, you end up with a straight line, not a triangle.