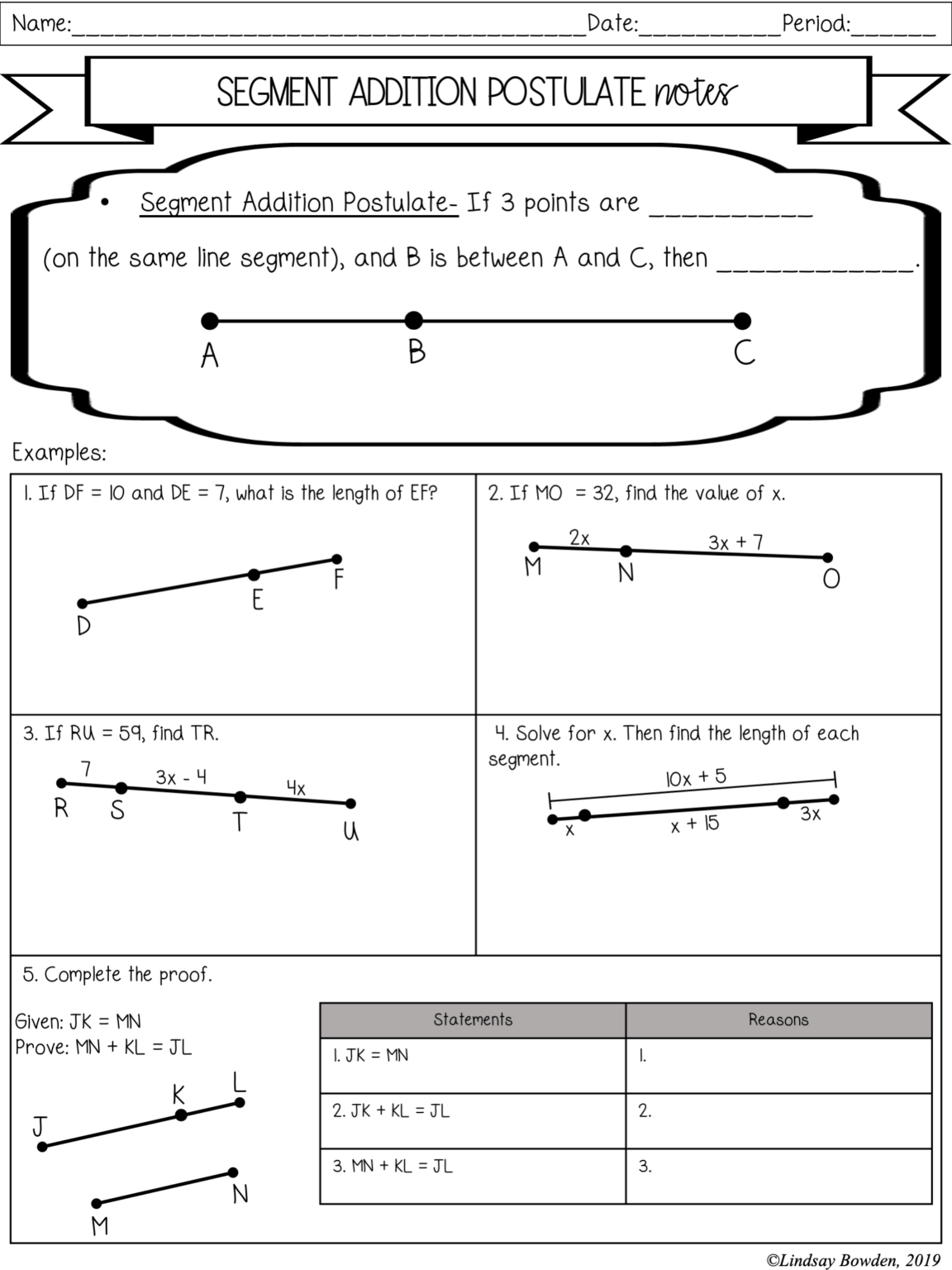
5 Essential Tips for Segment Addition Postulate Worksheets

In the realm of geometry, mastering the Segment Addition Postulate is fundamental for students. This principle helps them understand how to work with segments on a line, which is crucial for solving various geometric problems. Here, we will delve into five essential tips that can significantly enhance the effectiveness of teaching and understanding Segment Addition Postulate worksheets. These tips are not just about learning the postulate but also about making the learning process enjoyable and practical for students.
Tip 1: Start with Visuals

Visual aids are powerful tools in education, particularly when teaching concepts that involve spatial relationships. Begin your worksheet by illustrating:
- Line segments with clear points labeled for reference.
- How segments can be split into smaller parts using points on the line.
- The addition of these parts back into the whole segment.
🖼️ Note: Visuals not only clarify the concept but also engage students visually, making it easier for them to remember and understand the principle.
Tip 2: Engage with Real-Life Examples

To make the concept of segment addition more relatable:
- Introduce scenarios where segment addition can be applied in daily life, like dividing a street into segments or measuring the length of a piece of wood before cutting it.
- Explain how these real-world examples correlate with the postulate.
By linking the postulate to practical applications, students see the value in what they are learning, which can significantly increase their interest and understanding.
Tip 3: Use Interactive Questions
Interactive questions help:
- Check for understanding in real-time.
- Engage students actively in the learning process.
- Assess their ability to apply the Segment Addition Postulate.
Here’s a sample of how to structure these questions:
| Segment | Points | Length of AB | Length of BC | Length of AC |
|---|---|---|---|---|
| AB | A, B, C | 5 units | 7 units | 12 units |
| Given that AB + BC = AC, what is BC if AB = 5 units and AC = 14 units? | ||||

Tip 4: Implement Peer Learning

Learning with peers can boost:
- Students’ comprehension through discussion.
- Communication skills as they explain concepts.
- Confidence as they solve problems together.
Include group activities where students work together to solve worksheet problems. Encourage them to teach each other, discuss strategies, and validate their answers as a team.
Tip 5: Make Use of Technology

Incorporating technology into worksheets can:
- Provide interactive elements like drag-and-drop for segment creation.
- Enhance visualization through digital tools.
- Offer immediate feedback, which is crucial for learning.
Consider using educational software or creating a digital worksheet with features like:
- Dynamic segments that students can manipulate.
- Interactive quizzes to check understanding in real-time.
In summary, mastering the Segment Addition Postulate worksheets requires not only understanding the concept but also engaging students in a way that makes the learning process memorable and practical. By utilizing visuals, real-life examples, interactive questions, peer learning, and technology, educators can create an environment where students are excited to explore geometry. These tips pave the way for students to apply the principles of the Segment Addition Postulate confidently to real-world scenarios, fostering a deeper connection with mathematics.
Why is the Segment Addition Postulate Important in Geometry?

+
The Segment Addition Postulate forms the foundation for understanding lengths and how segments interact on a line, crucial for advanced geometry topics like area, perimeter, and transformations.
Can I Solve Segment Addition Problems without Using the Postulate?

+
While you might solve some basic problems without explicitly stating the postulate, using it provides a structured approach to ensure accuracy in geometric proofs and calculations.
How Can Teachers Make Learning the Segment Addition Postulate Fun?

+
Teachers can incorporate games, technology, and real-world applications to engage students, making the learning process interactive and enjoyable.



