Quadratic Formula Answer Key: 5 Simplified Solutions

Embarking on a journey through algebraic equations can often lead us to the quadratic formula, a fundamental tool for solving problems of the form ax^2 + bx + c = 0. This formula isn't just about finding the roots of a quadratic equation; it's a bridge to understanding how various mathematical concepts interlace with each other, offering a deeper appreciation for the intricacies of algebra. In this long-form blog post, we'll explore not only the derivation of the quadratic formula but also delve into five simplified approaches to master it effectively.
Understanding the Quadratic Formula

At its core, the quadratic formula provides the solution for x in the quadratic equation:
[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} ]
Here, a, b, and c are the coefficients from the standard form of the quadratic equation ax^2 + bx + c = 0.
What does each part signify?
- The Numerator: -b \pm \sqrt{b^2 - 4ac} - This part calculates the roots of the equation, with the discriminant b^2 - 4ac indicating the nature of the roots (real or complex).
- The Denominator: 2a - This normalizes the solution, accounting for the coefficient of x^2.
🔍 Note: The discriminant b^2 - 4ac can be zero, positive, or negative, leading to a single real root, two distinct real roots, or two complex conjugate roots, respectively.
Five Simplified Approaches to Mastering the Quadratic Formula
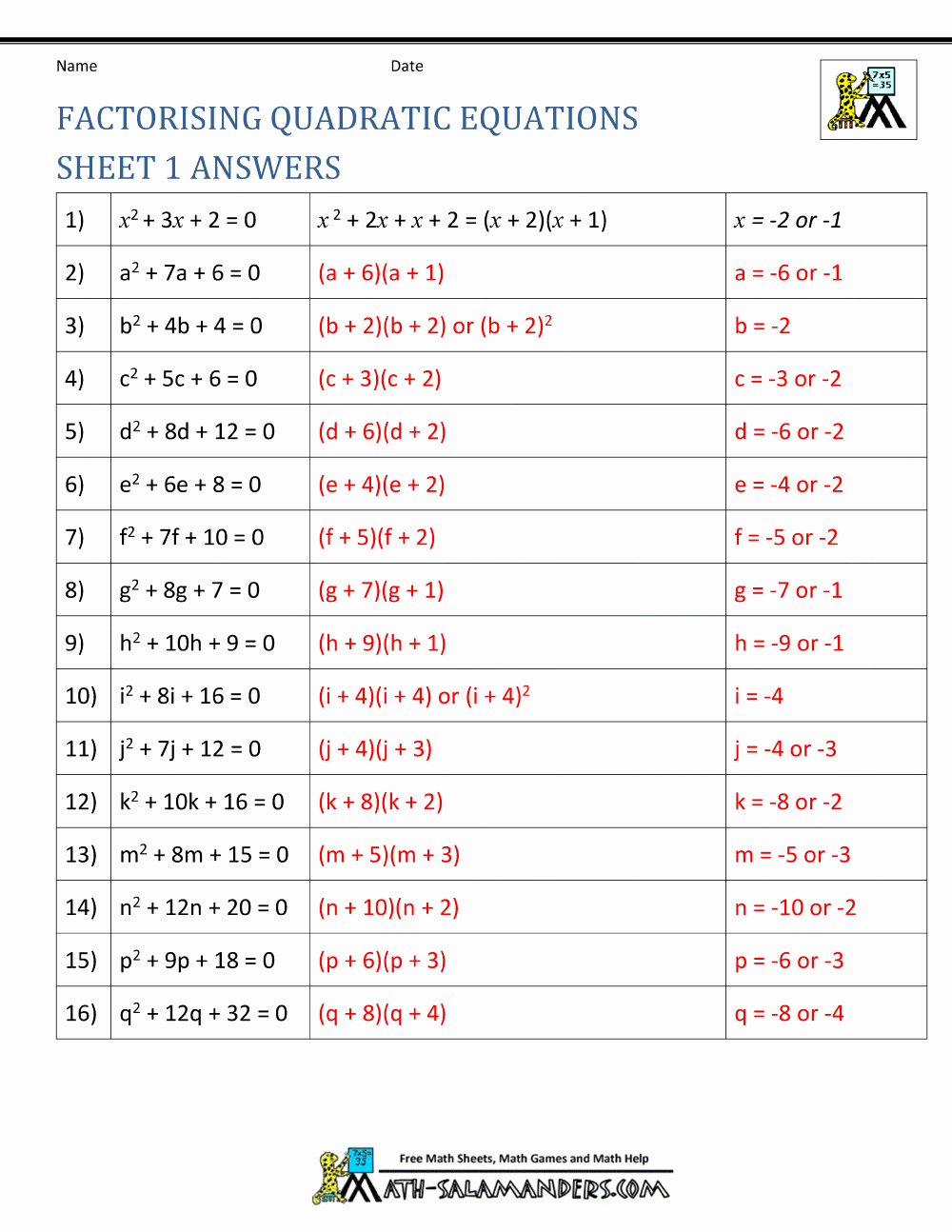
1. Practice with Simpler Equations

The first step towards mastering the quadratic formula is practice, and what better way than starting with equations where coefficients are easy to handle:
- Use equations like x^2 + 5x + 6 = 0 or x^2 - x - 2 = 0 where a = 1 to reduce complexity initially.
2. Utilize Patterns and Symmetry

Quadratic equations often exhibit symmetry and patterns:
- Look for equations where b = 0 (e.g., x^2 - c = 0), simplifying the solution process by removing one part of the equation.
- Notice how equations like x^2 + bx = 0 or ax^2 + c = 0 directly influence the formula's structure.
3. Use Technology as a Learning Tool

Modern technology provides tools to reinforce learning:
- Use graphing calculators or online tools to visualize the roots of quadratic equations, aiding in the understanding of why solutions work.
📱 Note: When using technology, ensure you understand the logic behind the operations; don't let technology substitute for understanding.
4. Study Deviations from the General Form

Not all quadratic equations will be presented in standard form:
- Practice identifying and rearranging equations like x^2 - 3x - 5 + 2x^2 = 0 to fit ax^2 + bx + c = 0.
| Original Equation | Standard Form |
|---|---|
| $x^2 - 3x - 5 + 2x^2 = 0$ | $3x^2 - 3x - 5 = 0$ |
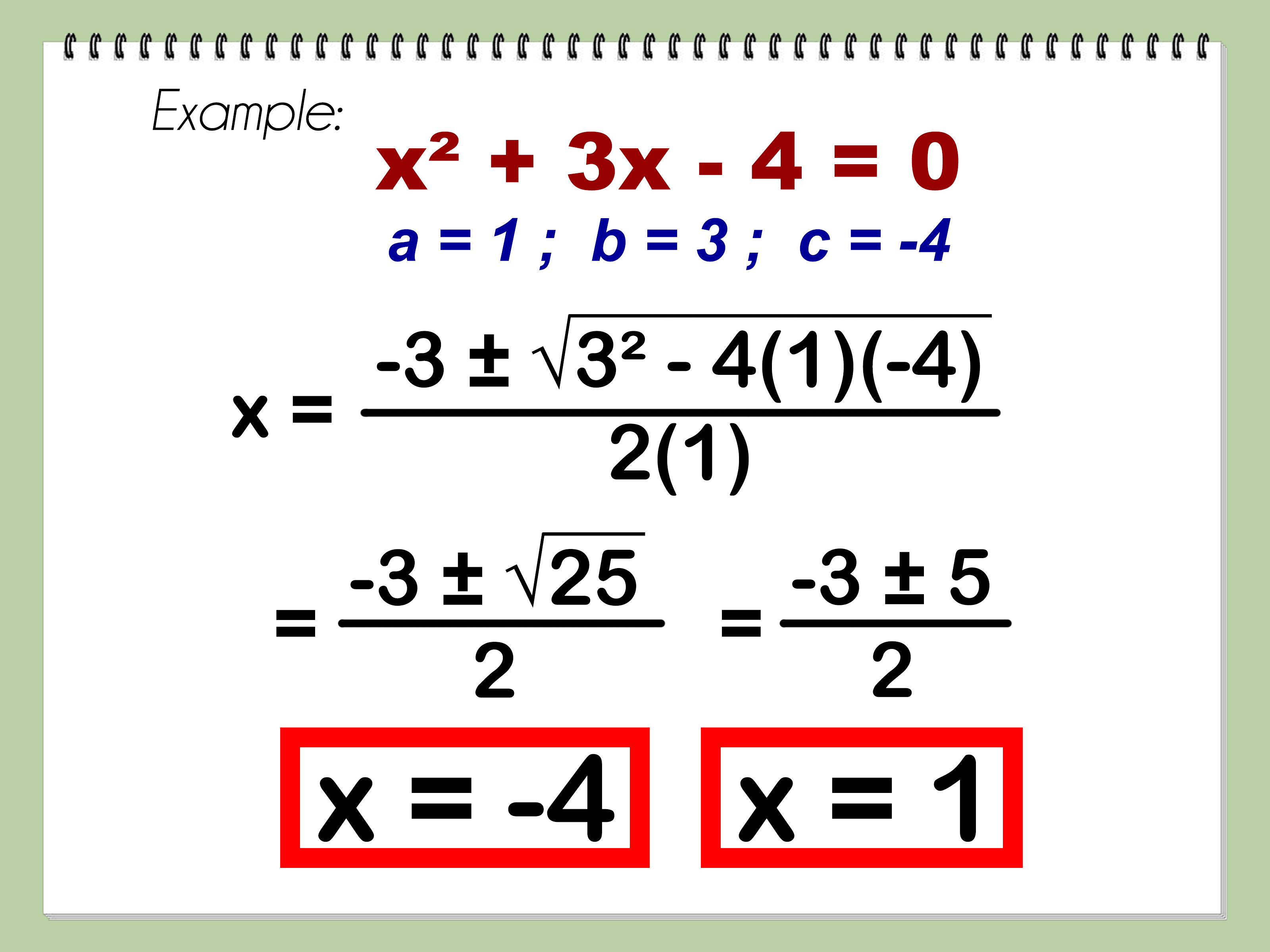
5. Relate to Real-World Scenarios

Applying the quadratic formula to real-world scenarios can enhance understanding:
- Model projectile motion, where time t is the solution to a quadratic equation related to height.
- Analyze business models to understand profit maximization or break-even points.
Throughout these approaches, the key is consistent practice. By engaging with the quadratic formula through these methods, you not only solve equations but also deepen your appreciation for how mathematics models and explains phenomena in the world around us. In summary, mastering the quadratic formula involves understanding its parts, practicing, leveraging patterns and technology, handling deviations from standard form, and connecting with real-world applications.
What is the quadratic formula used for?

+
The quadratic formula is primarily used to solve quadratic equations of the form (ax^2 + bx + c = 0) to find the values of (x) (roots or solutions) where the equation equals zero.
How do you know if the roots are real, imaginary, or equal?

+
The discriminant ((b^2 - 4ac)) determines this: - If (b^2 - 4ac > 0), there are two distinct real roots. - If (b^2 - 4ac = 0), there is one real root (the roots are equal). - If (b^2 - 4ac < 0), the roots are imaginary (complex conjugates).
Can the quadratic formula be used with any coefficients?

+
Yes, the quadratic formula is universal for solving quadratic equations with any real coefficients (a), (b), and (c). However, if (a = 0), the equation becomes linear and does not require the quadratic formula.