5 Tips for Mastering the Midpoint Formula Easily

Embarking on the journey to understand and effectively use the midpoint formula is essential for anyone delving into the world of geometry, algebra, or even computer graphics. This tool is not just a mathematical concept; it's a fundamental skill that aids in solving various problems. Here are five practical tips that can help you master the midpoint formula with ease:
Understand the Concept

Before you dive into using the midpoint formula, ensure you grasp what it represents:
- Midpoint Definition: The midpoint of a line segment is the exact center point between two endpoints, (x1, y1) and (x2, y2).
- Midpoint Formula: The formula is (xM = (x1 + x2)/2, yM = (y1 + y2)/2), where (xM, yM) is the midpoint.
🔍 Note: The midpoint divides the line segment into two equal parts, making it a pivotal concept in geometry and coordinate systems.
Practice with Examples

The best way to become proficient is through practice. Here's how you can practice:
- Start with simple coordinates, like finding the midpoint between (1, 1) and (3, 3).
- Progress to more complex coordinates to solidify your understanding.

👓 Note: Use online tools or graph paper to visually confirm your calculations, enhancing your spatial understanding.
Use Visual Aids

Visual learning can be incredibly effective:
- Employing graph paper or digital tools to plot points and visually locate midpoints can solidify your understanding.
- Online graphing calculators: Platforms like Desmos can dynamically illustrate midpoints for you.
Link the Midpoint to Real-Life Applications

Understanding how the midpoint formula applies to real-world situations can make it more interesting:
- Geographic coordinates: Finding a meeting point between two locations.
- Video games: Programming collision detection, character positioning, or NPC movement.
| Application | Description |
|---|---|
| City Planning | Determining a central location for amenities like parks or public transport. |
| Art and Design | Creating symmetrical patterns or finding the center of canvas. |

Make Connections to Other Mathematical Concepts

Linking the midpoint formula to other areas of math can deepen your understanding:
- Distance Formula: The midpoint formula helps calculate the halfway point when finding distances between two points.
- Line Segments: Midpoints are crucial in understanding segments, division, and ratios.
📐 Note: Understanding the midpoint formula also facilitates the comprehension of geometric transformations like reflections and symmetry.
As you conclude this journey through mastering the midpoint formula, remember that like any skill, it requires consistent practice. Use these tips as your guide to not only understand but apply the midpoint formula effectively. Whether you're calculating distances, positioning characters in a game, or simply exploring the geometry of your surroundings, the midpoint formula provides a simple yet powerful tool for solving spatial problems.
What does the midpoint formula represent?

+
The midpoint formula finds the point that is exactly between two given points on a straight line, dividing it into two equal parts.
How can I practice finding midpoints?
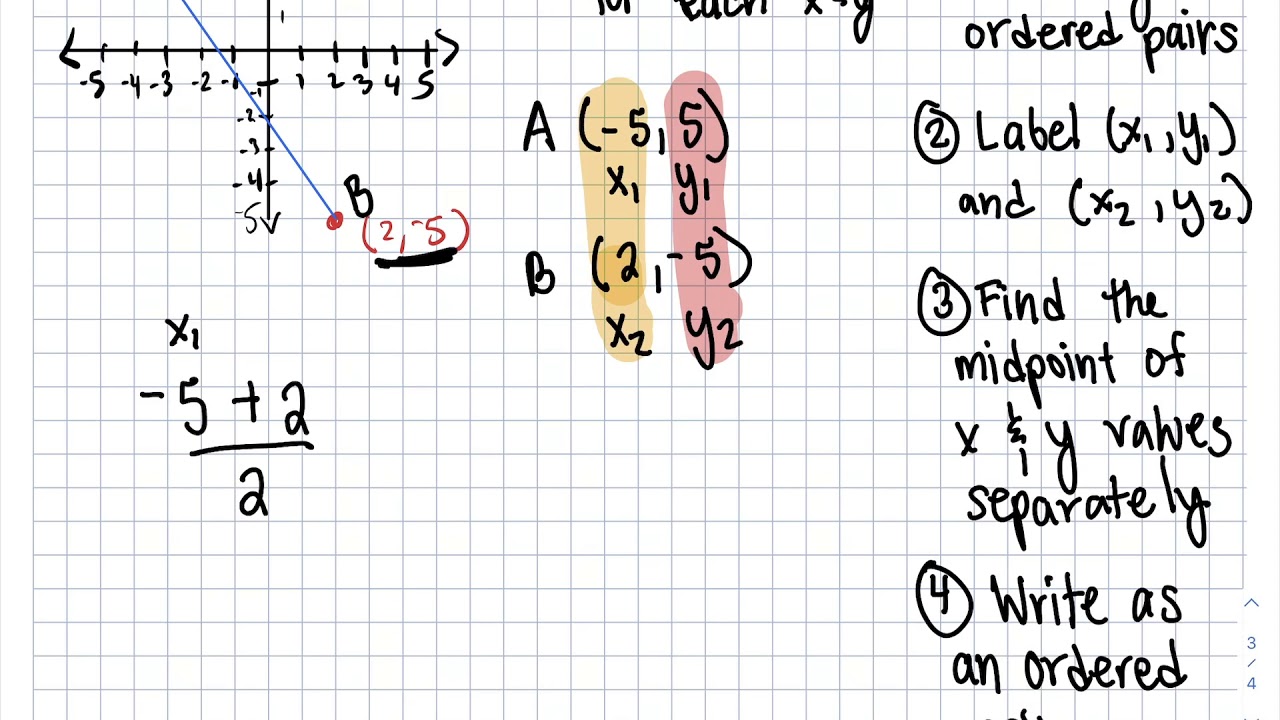
+
Practice with a variety of coordinates. Start simple, then increase complexity. Use online tools or graph paper to visually confirm your calculations.
Why is understanding the midpoint formula important?

+
It’s crucial in many fields including geometry, algebra, computer graphics, and even real-life applications like navigation or city planning for finding central locations or distances.
What are some real-world applications of the midpoint formula?

+
From city planning to video games, the midpoint formula is used to determine central locations, ensure symmetrical designs, or calculate distances in diverse fields.
Can the midpoint formula be extended to three-dimensional space?

+
Yes, the formula can be extended to three dimensions using the average of x, y, and z coordinates as (xM, yM, zM).



