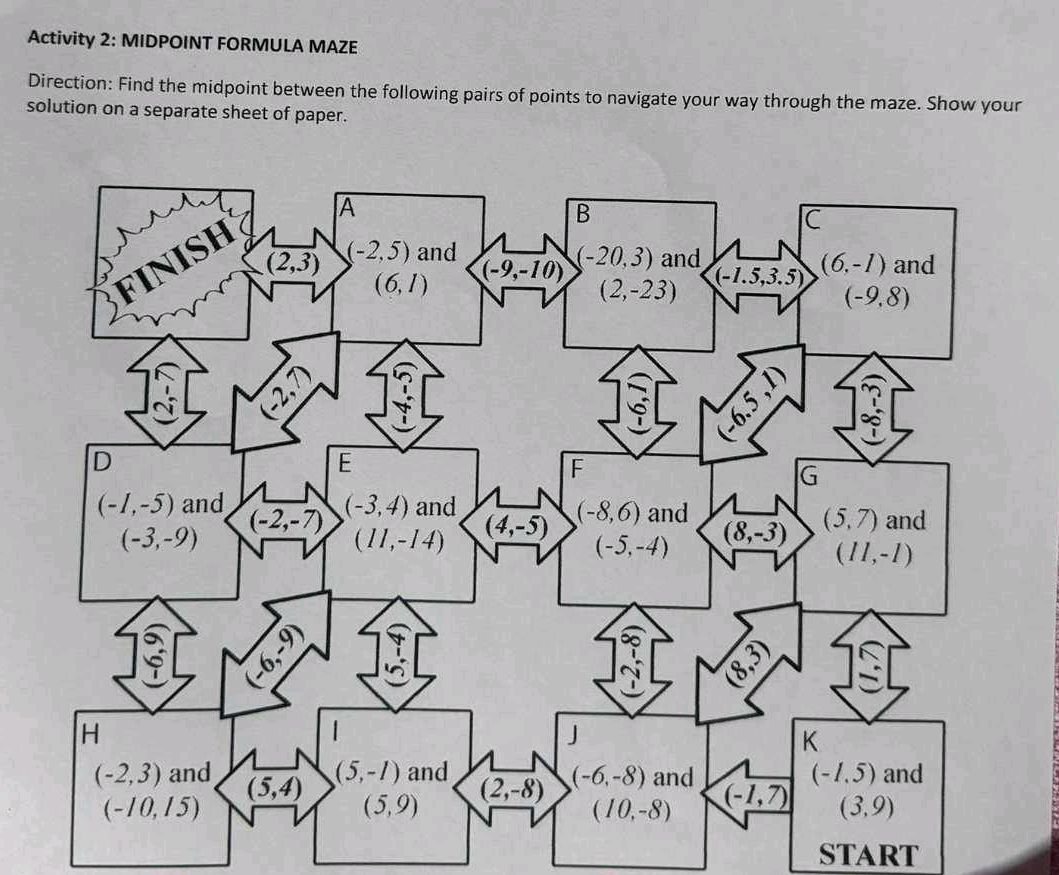
Midpoint Formula Maze Worksheet Answers Revealed

Welcome to the labyrinth of the Midpoint Formula Maze Worksheet. Whether you're a student looking for answers or an educator seeking an alternative solution guide, this detailed walkthrough will serve as your beacon through the mathematical maze. The midpoint formula, crucial in coordinate geometry, determines the exact middle point between any two given points. Here, we'll explore how to use this formula in various settings, not just to solve problems but to understand and appreciate the underlying principles of geometry.
Understanding the Midpoint Formula

The midpoint formula is a fundamental equation in coordinate geometry, expressed as:
[ M = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) ]
Where (x_1, y_1) and (x_2, y_2) are the coordinates of the two endpoints. To find the midpoint, you simply average the x-coordinates and the y-coordinates. Here's a quick breakdown:
- Step 1: Sum the x-coordinates.
- Step 2: Sum the y-coordinates.
- Step 3: Divide each sum by 2.
🎓 Note: The formula calculates the midpoint, which splits the line segment into two equal parts.
Navigating the Maze: Worksheet Answers

Let’s solve some of the common problems you’ll encounter in a midpoint formula maze worksheet:
Example Problem: Find the midpoint between (2, 3) and (8, 7)

- Sum the x-coordinates: 2 + 8 = 10 .
- Sum the y-coordinates: 3 + 7 = 10 .
- Divide each sum by 2: \frac{10}{2} = 5 .
- Thus, the midpoint M is (5, 5) .
| Coordinates | Sum | Midpoint Calculation |
|---|---|---|
| (2, 3) | 2 + 8 = 10 3 + 7 = 10 |
M = (5, 5) |
🧭 Note: Remember to consistently divide by 2 to get the midpoint correctly.
Example Problem: Find the midpoint between (-4, 5) and (2, -3)

- Sum the x-coordinates: -4 + 2 = -2 .
- Sum the y-coordinates: 5 + (-3) = 2 .
- Divide each sum by 2: \frac{-2}{2} = -1 and \frac{2}{2} = 1 .
- Therefore, the midpoint M is (-1, 1) .
📌 Note: Negative coordinates and positive coordinates cancel each other out when averaging.
Example Problem: Determine the midpoint given endpoints with larger numbers

Imagine two points are at (6, 10) and (14, 22):
- Sum the x-coordinates: 6 + 14 = 20 .
- Sum the y-coordinates: 10 + 22 = 32 .
- Divide each sum by 2: \frac{20}{2} = 10 and \frac{32}{2} = 16 .
- The midpoint M is (10, 16) .
More Complex Scenarios
In some maze worksheets, the problems can get more intricate:
Example Problem: Given the midpoint and one endpoint, find the other endpoint

If you know the midpoint is (3, 4) and one endpoint is (0, 0), calculate the other endpoint:
- Let (x_1, y_1) be (0, 0) and (x_2, y_2) be the unknown endpoint.
- From the midpoint formula: \[ 3 = \frac{0 + x_2}{2} \quad \text{and} \quad 4 = \frac{0 + y_2}{2} \]
- Solve for x_2 and y_2 : \[ x_2 = 6 \quad \text{and} \quad y_2 = 8 \]
- Therefore, the other endpoint is (6, 8).
🔍 Note: This problem demonstrates how the midpoint can help determine missing coordinates.
Final Thoughts
We’ve now navigated through several examples of midpoint formula problems commonly found in maze worksheets. The key is understanding how the formula works: averaging the coordinates to find the midpoint. With practice, these problems become not just exercises in calculation but opportunities for insight into geometric principles. Whether you’re solving for the midpoint, or using the midpoint to find an unknown endpoint, the underlying math remains consistent and elegant.
Why is the midpoint formula useful in geometry?

+
The midpoint formula is essential for understanding line segments, medians, and partitioning segments. It provides insight into the center point of any given line, which is crucial in both theoretical geometry and practical applications like surveying or computer graphics.
Can I use the midpoint formula with different dimensions?

+
Yes, while most commonly used in 2D, the midpoint formula can be adapted for higher dimensions by taking the average of the corresponding coordinates in each dimension.
What if one of the endpoints is on an axis?

+
If an endpoint lies on an axis, the midpoint will still be calculated normally. However, if the endpoint is at the origin (0, 0), the midpoint will be half of the other endpoint’s coordinates.