Tangent Ratio: 5 Steps to Master Key Worksheet Answers
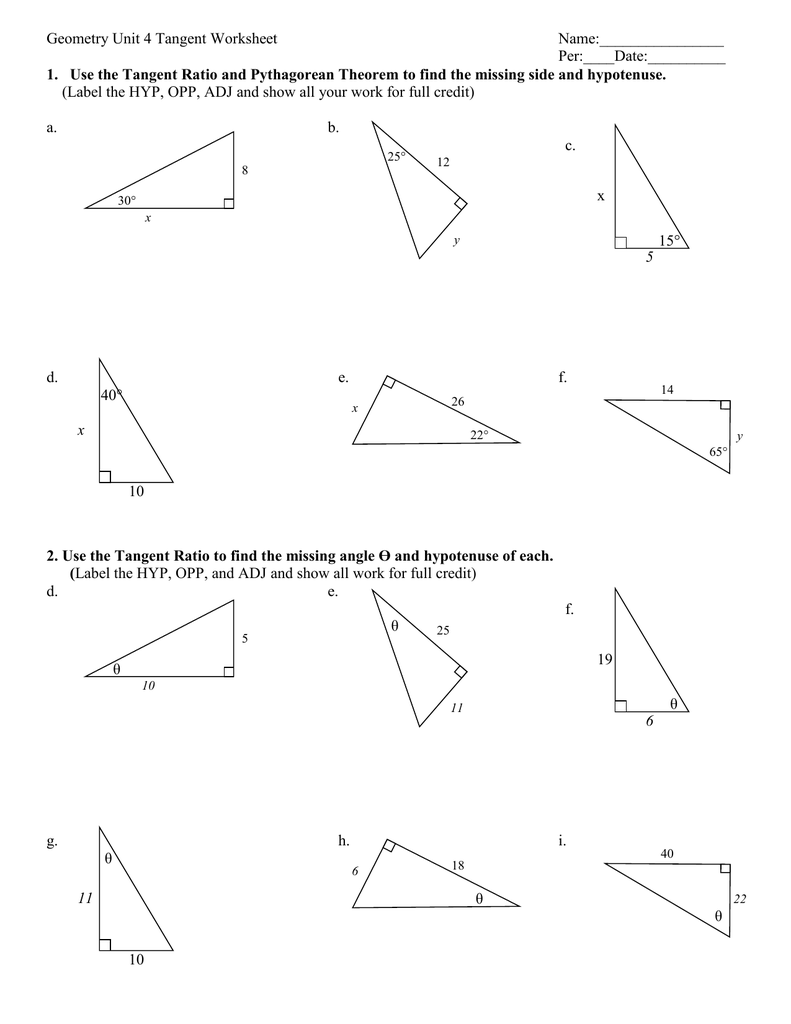
Understanding the tangent ratio is fundamental for students delving into trigonometry. This mathematical concept not only helps in solving complex problems but also fosters a deeper understanding of angles and their relationships in triangles. Here are five steps to guide you through mastering the tangent ratio in your key worksheet answers for an enriching learning experience:
1. Grasp the Basics of Tangent

The tangent of an angle in a right triangle is defined as the ratio of the length of the opposite side to the length of the adjacent side. Here's how you can start understanding this:
- Opposite Side: The side opposite the angle of interest.
- Adjacent Side: The side next to the angle of interest, but not part of the hypotenuse.
The formula for tangent is: \[ \tan(\theta) = \frac{\text{Opposite}}{\text{Adjacent}} \]
2. Practice with Diagrams

Using diagrams to visualize the relationship between angles and sides can significantly enhance your understanding. Here are a few techniques:
- Label the sides of your triangle as per the angle of interest.
- Calculate the tangent for different angles by measuring or identifying known sides.
Below is a simple example of how you might calculate the tangent for an angle:
| Angle | Opposite | Adjacent | Tangent |
|---|---|---|---|
| 30° | 1 | √3 | 1 / √3 ≈ 0.58 |
| 45° | 1 | 1 | 1 / 1 = 1 |

⚠️ Note: Always ensure that the triangle you're working with is a right triangle.
3. Solving Tangent Problems

Now that you're familiar with the concept, solving problems becomes more approachable. Follow these steps:
- Identify: Which angle are you solving for?
- Set Up: Write down the tangent ratio equation.
- Solve: Manipulate the equation to find the missing side or angle.
Here's an example problem:
Given a triangle with an angle of 37°, and the adjacent side being 5 units, find the opposite side:
- \[ \tan(37°) = \frac{\text{Opposite}}{5} \]
- Looking up \tan(37°) in a table or using a calculator, we find \tan(37°) \approx 0.75
- \text{Opposite} = 0.75 \times 5 \approx 3.75 units
4. Angle Verification

Ensure your calculations are correct by verifying angles:
- Use a protractor or angle finder tool to check the angle.
- Verify using the inverse tangent function: If \tan(\theta) = \text{Ratio}, then \theta = \arctan(\text{Ratio}).
5. Mastery through Repetition and Application

The key to mastering the tangent ratio is consistent practice:
- Solve various types of problems including word problems where you need to apply tangent ratios.
- Use real-life applications like calculating slopes or heights of buildings to contextualize your learning.
- Join study groups or seek tutoring to discuss and resolve any doubts.
The path to mastering the tangent ratio involves more than just memorizing formulas; it's about understanding the underlying principles and applying them. Regular practice, combined with a strong foundation in basics, will lead to proficiency in tackling trigonometry problems. As you progress, the relationships between angles and sides become intuitive, allowing you to approach more complex scenarios with confidence and precision.
Why is understanding the tangent ratio important in trigonometry?

+
Tangent ratios are essential for understanding how angles and lengths relate within triangles, enabling you to solve for unknown sides or angles, which is fundamental for many areas in mathematics, science, and engineering.
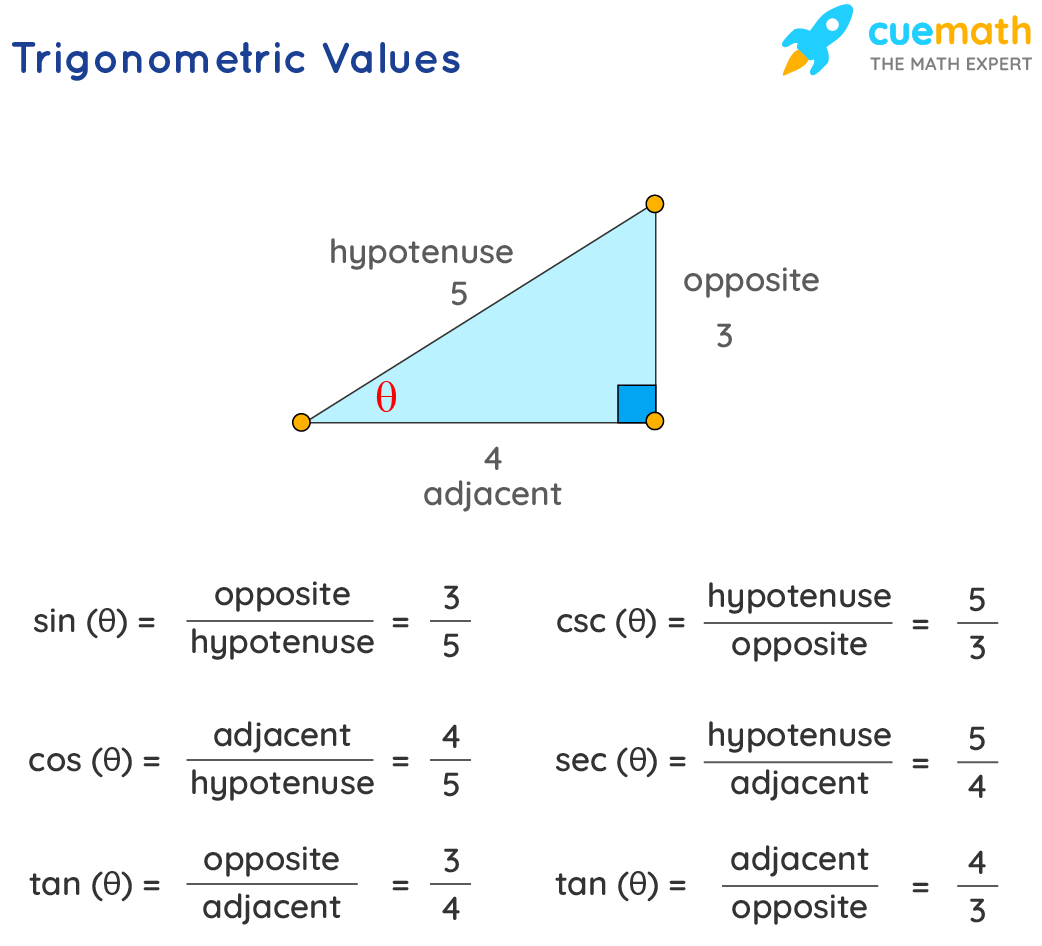
How can I remember the tangent formula?
+
Remember the mnemonic “SOHCAHTOA,” where “SOH” stands for Sine Opposite Hypotenuse, “CAH” for Cosine Adjacent Hypotenuse, and “TOA” for Tangent Opposite Adjacent. The tangent part (TOA) helps you recall that tangent is opposite over adjacent.
Can the tangent of an angle be greater than 1?

+
Yes, the tangent of an angle can be greater than 1. As the angle increases beyond 45°, the length of the opposite side becomes larger than that of the adjacent, resulting in a tangent value greater than 1.
What are some common real-life applications of the tangent ratio?

+
Applications include calculating the height of inaccessible objects like trees or buildings by measuring their angles of elevation from a known distance, determining slopes in construction or architecture, and in computer graphics for perspective drawing.
What if I’m confused about which side is opposite or adjacent in a problem?

+
Always label the angles in the triangle and identify the reference angle for which you’re solving. Remember: the opposite side is across from the angle, and the adjacent side is next to the angle but not part of the hypotenuse.