Solve Linear Equations Worksheet: Easy Guide for Beginners

The ability to solve linear equations is a fundamental skill in mathematics, providing a foundation for understanding more complex algebraic problems. Linear equations are not only an essential part of algebra but are also relevant in real-world scenarios, from budgeting personal finances to analyzing data trends in science and business. This guide is designed to walk beginners through the process of solving these equations step by step, ensuring a clear and practical understanding of each concept.
What is a Linear Equation?

A linear equation is an algebraic equation where each term is either a constant or the product of a constant and a single variable. Here’s a look at the standard form:
- ax + b = c, where:
- a, b, and c are constants (with a not being zero).
- x is the variable.
Types of Linear Equations

Linear equations come in various forms, but beginners generally encounter these:
- One-Step Equations: Where you only need one operation (addition, subtraction, multiplication, or division) to solve.
- Two-Step Equations: These require two operations to find the solution.
- Multi-Step Equations: These involve more than two steps, combining multiple operations or applying the distributive property.
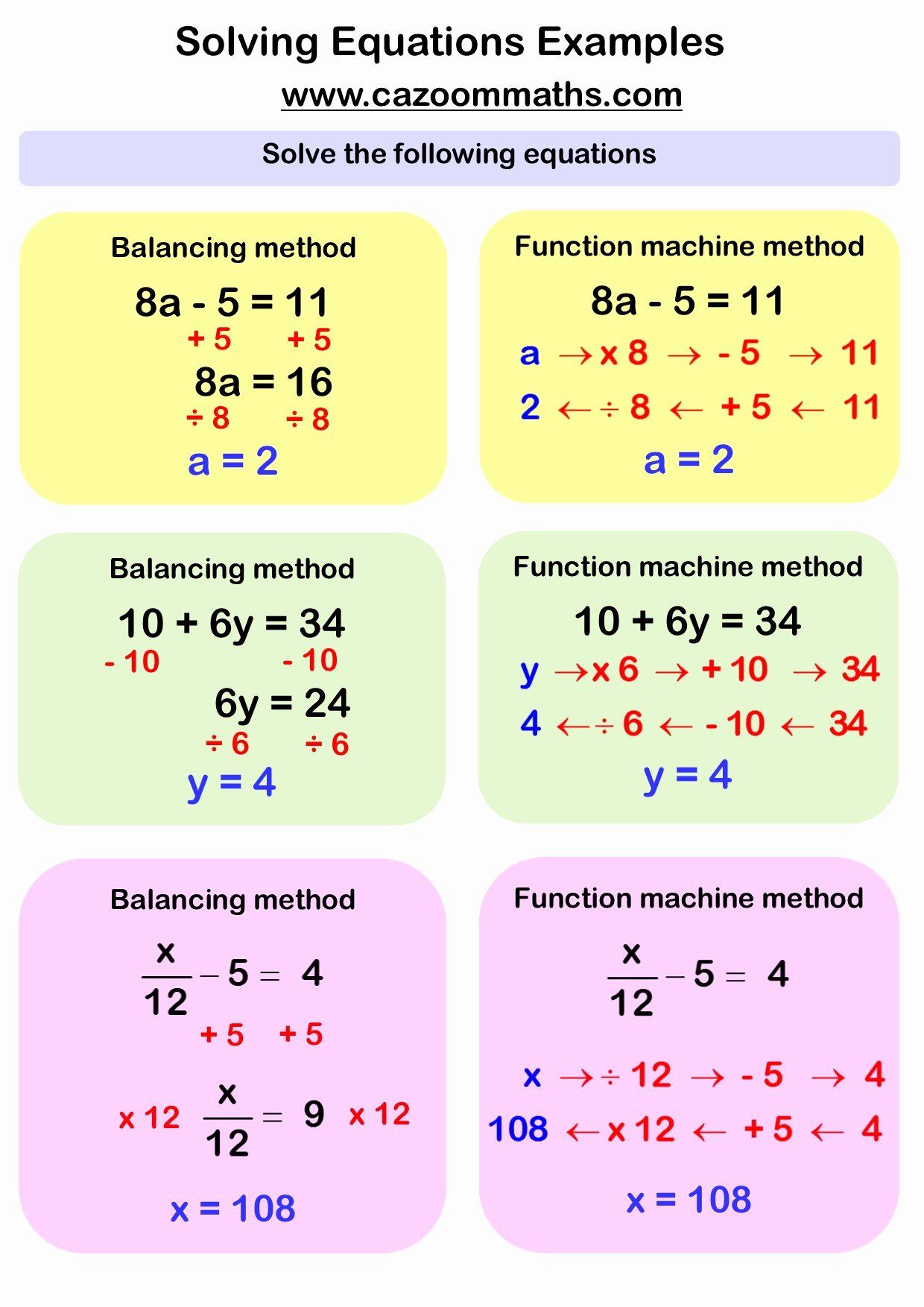
Step-by-Step Guide to Solving Linear Equations

1. One-Step Equations

These equations involve isolating the variable through a single operation. Here are the steps:
- Identify the operation: Determine what operation is needed to isolate the variable.
- Apply the inverse operation: Use the opposite operation to undo what's being done to the variable.
Example: Solve for x in x + 5 = 10
- Operation: Subtraction (-5).
- Apply the inverse operation: x + 5 - 5 = 10 - 5, simplifies to x = 5.
⚠️ Note: The goal is always to isolate the variable on one side of the equation.
2. Two-Step Equations

These require combining basic algebra rules to solve:
- Eliminate constants first: Add or subtract constants to isolate the term with the variable.
- Solve for the variable: Then, multiply or divide to find the value of the variable.
Example: Solve for x in 3x + 2 = 11
- Step 1: Subtract 2 from both sides to isolate the term with the variable: 3x + 2 - 2 = 11 - 2, simplifies to 3x = 9.
- Step 2: Divide both sides by 3 to solve for x: (3x)/3 = 9/3, simplifies to x = 3.
3. Multi-Step Equations

More involved than the previous, these require careful application of all algebra rules:
- Combine like terms: Simplify the equation by combining terms on each side.
- Use the distributive property if necessary: If there's a parenthesis, distribute the constant outside to terms inside.
- Follow the steps for two-step equations: Then apply operations to isolate and solve for the variable.
Example: Solve for x in 2(x + 3) + 4 = 18
- Step 1: Distribute the 2: 2x + 6 + 4 = 18, simplifies to 2x + 10 = 18.
- Step 2: Subtract 10 from both sides: 2x + 10 - 10 = 18 - 10, simplifies to 2x = 8.
- Step 3: Divide both sides by 2: (2x)/2 = 8/2, simplifies to x = 4.
Checking Solutions

After solving, it's always good practice to verify your answer:
- Substitute the solution back into the original equation.
- If both sides of the equation balance, your solution is correct.
Example:
Solve 2x + 5 = 11
- Solution is x = 3.
- Substitute back: 2(3) + 5 = 6 + 5 = 11, confirming the solution is correct.
💡 Note: Verifying solutions ensures your accuracy in algebraic calculations, crucial for mastering complex equations.
Common Pitfalls and Tips

Here are some common mistakes beginners make and tips to avoid them:
- Not isolating the variable: Always ensure you isolate the variable on one side.
- Forgetting the distributive property: If there's a parenthesis, distribute the constant outside.
- Misunderstanding signs: Be careful with positive and negative signs, especially when subtracting or adding negatives.
Tips:

- Write each step clearly to avoid confusion.
- Check your work by substituting back into the equation.
- Understand the concept of balancing equations; whatever operation you perform on one side, do the same on the other.
This beginner's guide has walked through solving linear equations with simplicity and clarity. From understanding the basic form to tackling multi-step equations, these skills lay the groundwork for more advanced algebraic concepts. Remember to practice, check your solutions, and understand the logic behind each step for a comprehensive grasp of linear equations.
Key takeaways include:
- Isolating variables to solve equations.
- Recognizing and using the inverse operation to solve equations.
- Verifying solutions by substitution.
- Avoiding common mistakes by following algebraic rules and understanding the process.
Why do we need to isolate the variable in an equation?

+
Isolating the variable on one side of the equation helps in directly finding the value that makes the equation true. This process simplifies complex equations into steps that are easier to manage.
What is the significance of the distributive property in solving equations?

+
The distributive property allows us to remove parentheses by multiplying the term outside the parenthesis to each term inside, simplifying the equation for easier solving.
Can you solve an equation with multiplication and division first?
+
When solving linear equations, you can address multiplication or division first if it helps simplify the equation, but you must do the same operation to both sides to maintain balance.