5 Graphing Hacks for Solving Systems of Equations
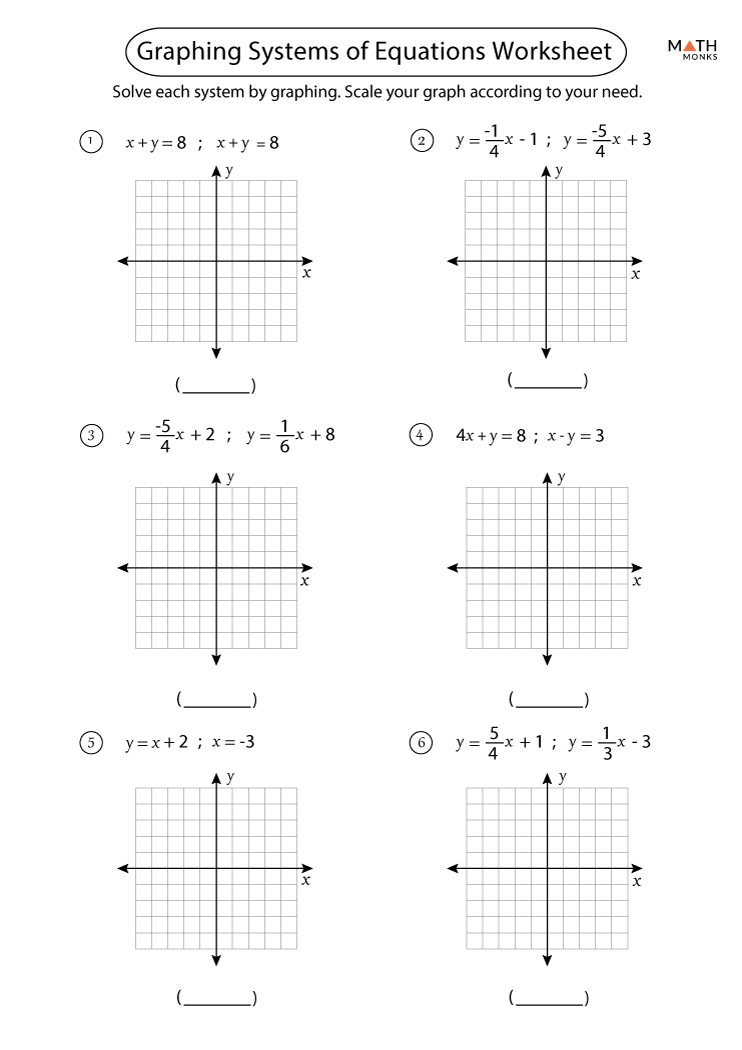
The art of solving systems of equations can be daunting, especially when dealing with multiple variables. However, with the right graphing techniques, you can significantly simplify this process. Here are five graphing hacks that can help you visualize and solve systems of equations more effectively:
1. Use a Graphing Calculator for Efficiency

A graphing calculator isn’t just a luxury; it’s a powerful tool for solving systems of equations:
- Input each equation into the calculator. Modern calculators like the TI-84 Plus can handle multiple functions simultaneously.
- Select the appropriate viewing window to see the intersection points clearly.
- Use the “intersection” function to find where the graphs of your equations meet.
📌 Note: Remember to check your calculator's manual or help guide for specific instructions on how to find intersections.
2. Leverage Slope-Intercept Form for Quick Comparison
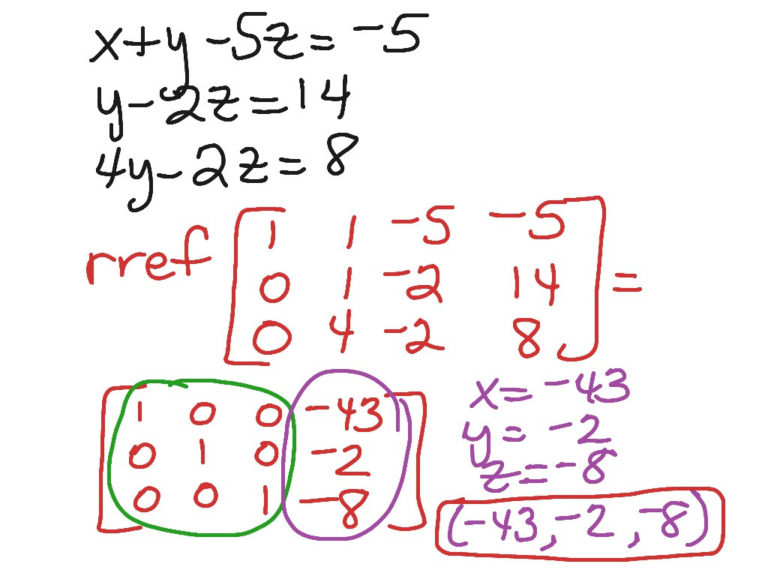
Converting equations to slope-intercept form (y = mx + b) offers several advantages:
- You can immediately see the slope (m) and y-intercept (b), making it easier to predict line behavior.
- Compare slopes directly to understand parallelism or perpendicularity.
- Graphing becomes straightforward as you plot the y-intercept and use the slope to plot additional points.
3. Sketch Rough Estimates to Save Time

Sometimes, precise graphing isn’t necessary to find a solution:
- Draw quick, rough sketches of your equations to visualize their general directions.
- Identify intersection regions without the need for accurate scales or axis labels.
- This method can help eliminate impossible solutions quickly.
📌 Note: This technique works best when you're looking for an approximate or conceptual solution rather than exact numbers.
4. Utilize Technology for Complex Graphs

For systems involving complex equations or inequalities:
- Use software like GeoGebra or Desmos for real-time graphing and solving.
- These tools can graph surfaces in 3D or visualize boundaries of inequalities with shading.
- Interactive sliders allow for adjusting parameters to see how equations change.
5. Enhance Your System with Linear Combination

Combine graphing with algebraic methods like linear combination for a two-pronged approach:
- Graph the equations to get a visual idea of possible solutions.
- Apply linear combination to eliminate one of the variables, making the system easier to solve.
- Check your algebraic solutions graphically to confirm their accuracy.
By integrating these graphing hacks into your mathematical toolkit, you'll find solving systems of equations becomes not only more manageable but also more intuitive. Each method provides a unique perspective, allowing you to tackle problems from different angles, thereby enhancing your problem-solving capabilities in algebra and beyond.
Can I solve systems of equations without graphing?

+
Yes, you can use algebraic methods like substitution, elimination, or matrix techniques to solve systems without graphing. However, graphing can often provide a visual confirmation or initial insight into the problem.
What if my equations do not intersect?

+
If your lines or curves do not intersect, it means there are no solutions to the system of equations, indicating they are parallel or have no common points.
How do I graph inequalities on a calculator?

+
Most graphing calculators allow you to graph inequalities by using the Y-editor to set up the inequality (e.g., y > 2x + 3). Select the appropriate shading for above or below the line.
Is there a software better than graphing calculators for solving systems?

+
Software like GeoGebra or Desmos can offer more features and flexibility, including 3D graphing and interactive elements, which might surpass what typical calculators provide.
🌟 Key Takeaways: Always approach system of equations with a multi-faceted strategy. Whether you’re utilizing graphing, algebraic methods, or a blend of both, remember that understanding the problem’s visual representation can lead to quicker and more insightful solutions.