Mastering 3-Variable Equations: Free Worksheet Guide

There's no denying the importance of mathematics in both academic and real-world problem-solving, with linear equations often forming the backbone of numerous disciplines. This comprehensive guide aims to equip you with the knowledge to solve three-variable equations, a common challenge in algebra that tests one's understanding of systems of equations. Whether you're looking to brush up on your algebra skills, aiding a student, or exploring these concepts for the first time, this guide, accompanied by a free worksheet, will walk you through the intricate steps involved in mastering 3-variable equations.
The Basics of Three-Variable Equations

Let's first address the essentials:
- Variables: In our case, there are three unknowns, typically denoted as x, y, and z.
- Equations: You will usually have three linear equations that link these variables.
- System of Equations: This consists of the set of equations you need to solve simultaneously.
Why Learn Three-Variable Equations?

Understanding these equations is not only a fundamental part of algebra but also has practical applications:
- They help model real-world problems where multiple variables influence an outcome.
- They're essential in fields like engineering, economics, and physics, where scenarios often involve several variables.
- Solving these equations hones problem-solving skills and critical thinking.
Steps to Solve Three-Variable Equations

Elimination Method

The elimination method involves eliminating one variable at a time:
- Step 1: Choose two equations to start with and eliminate one variable by adding or subtracting them.
- Step 2: Use the third equation with one of the remaining equations to eliminate the same variable.
- Step 3: Solve the resulting two-variable system.
- Step 4: Substitute the values into one of the original equations to find the third variable.
📝 Note: Always ensure that your choice of equations to eliminate a variable doesn't inadvertently cancel out all variables, leading to an identity or contradiction.
Substitution Method
![[100% Off] Mastering One-Variable Equations [100% Off] Mastering One-Variable Equations](https://support.althea.net/assets/img/100-off-mastering-one-variable-equations.jpeg)
An alternative approach is the substitution method:
- Step 1: Solve one equation for one of its variables.
- Step 2: Substitute this expression into the other two equations, reducing them to a two-variable system.
- Step 3: Solve the system of the remaining equations.
- Step 4: Use the solution to find the remaining variable from the first equation.
📝 Note: Substitution is particularly useful when one of your equations has a variable already isolated or when it can be easily manipulated to isolate a variable.
Practical Examples and Worksheet

To solidify your understanding, here are some examples:
- Example 1: Solving for x, y, and z where:
- x + y + z = 10
- 2x + y - z = 4
- x - 2y + 3z = -1
| Variable | Value |
|---|---|
| x | 3 |
| y | 4 |
| z | 3 |
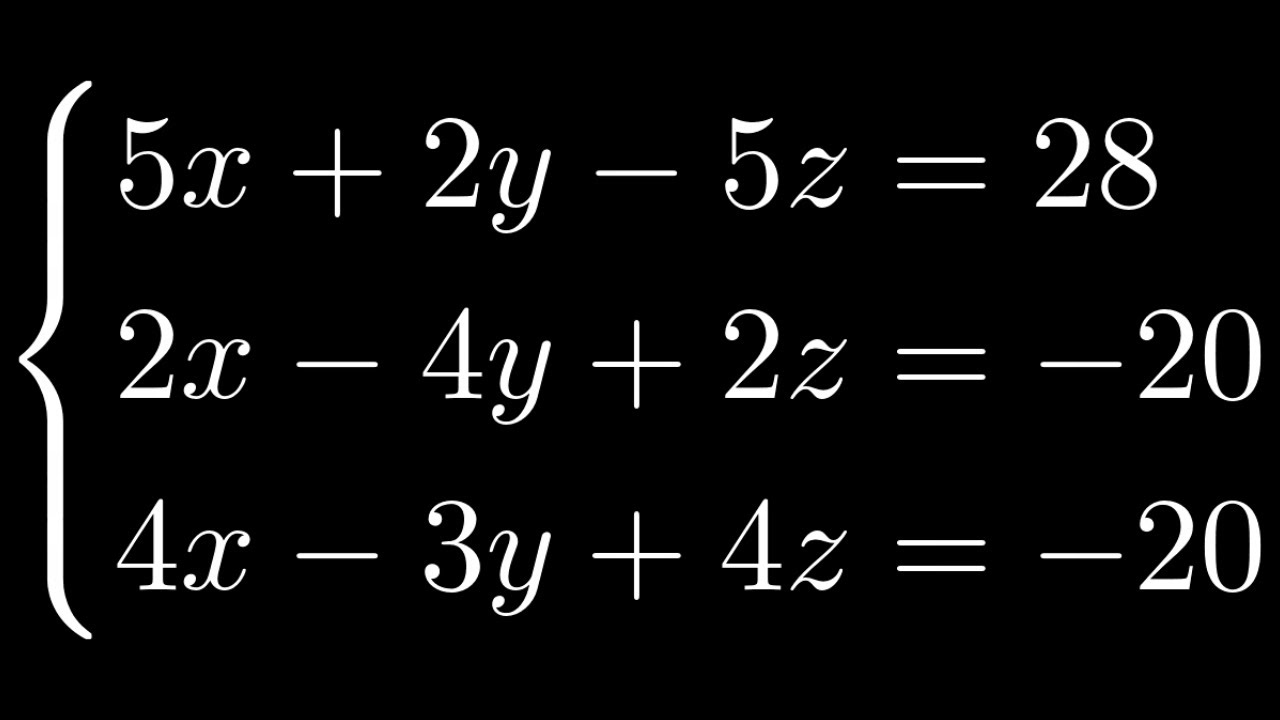
The accompanying free worksheet offers you the opportunity to practice these methods. It includes:
- Step-by-step problems with solutions.
- Varied problems to challenge different aspects of solving three-variable equations.
Tips for Solving

To improve your problem-solving skills:
- Check your work: Substitute your solutions back into the original equations to ensure they satisfy all conditions.
- Consider all possibilities: Equations can have unique solutions, no solution, or infinitely many solutions.
- Understand the geometry: These systems can be interpreted as intersections of planes in three-dimensional space.
📝 Note: Remember that while solving these equations, if you encounter contradictions, it means the system has no solution, and if you find an identity, it suggests infinite solutions.
As we wrap up, mastering three-variable equations is not just about solving math problems; it's about developing a toolkit for analyzing and understanding complex scenarios. Through the systematic approach of elimination or substitution, you can tackle seemingly intricate mathematical structures, reducing them to manageable components. The provided worksheet will offer practical experience, reinforcing your skills. Remember, the key to mastery lies in consistent practice, understanding the underlying principles, and checking your work. May your journey into the world of algebra be both enlightening and empowering.
What are the most common methods for solving 3-variable equations?

+
The two most common methods are the elimination method, where you systematically eliminate variables by adding or subtracting equations, and the substitution method, where you solve for one variable in terms of the others and substitute it into the other equations.
Can three-variable equations have more than one solution?

+
Yes, they can. The system might have:
- Unique Solution: Where the three planes intersect at a single point.
- No Solution: If the planes are parallel or intersect in such a way that they do not have a common point of intersection.
- Infinite Solutions: If the equations describe the same plane or set of planes that overlap in lines or areas.
Is there a graphical method to visualize three-variable equations?

+
Graphically, these equations can be represented as planes in 3D space. The solutions are where these planes intersect. For a better visualization, you can use graphing calculators or computer algebra systems to plot these planes and see their intersections.



