Surface Area Worksheet Answers: Quick and Easy Guide

Calculating surface area is a fundamental skill in geometry, particularly when dealing with three-dimensional shapes. Whether you're a student looking to reinforce your understanding, a teacher seeking to provide clear solutions, or simply someone interested in the math behind these calculations, having access to surface area worksheet answers can greatly enhance your learning or teaching experience. This guide offers a thorough look at how to find the surface area of common geometric figures like cubes, rectangular prisms, cylinders, and spheres, providing step-by-step instructions and addressing common pitfalls.
Understanding Surface Area

Before diving into specific shapes, it’s important to understand what surface area is:
- Surface area is the total area that the surface of the shape occupies. Think of it as the amount of paper you would need to cover the entire exterior of the shape without overlapping.
- It differs from volume, which measures the space inside the shape.
🌟 Note: Surface area is usually measured in square units (like m², cm²).
Surface Area of a Cube
A cube is one of the simplest shapes with which to calculate surface area because all its faces are identical squares.
| Formula | Area Calculation |
|---|---|
A = 6a2 |
Where A is the total surface area, and a is the side length of the cube. |

Here's how to calculate it:
- Identify the side length (let's say it's
a). - Square the side length to find the area of one face.
- Multiply this by 6 to account for all faces of the cube.
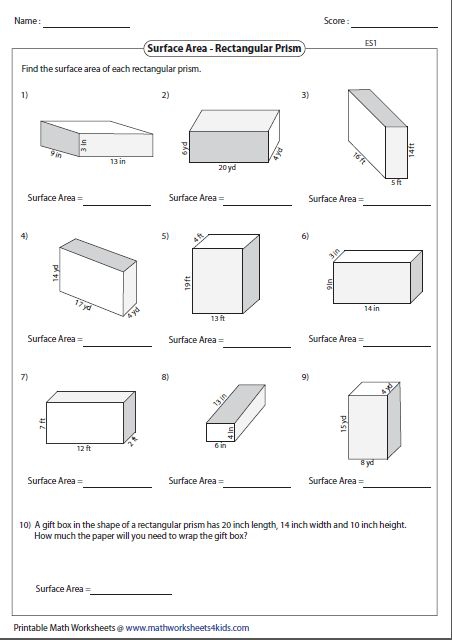
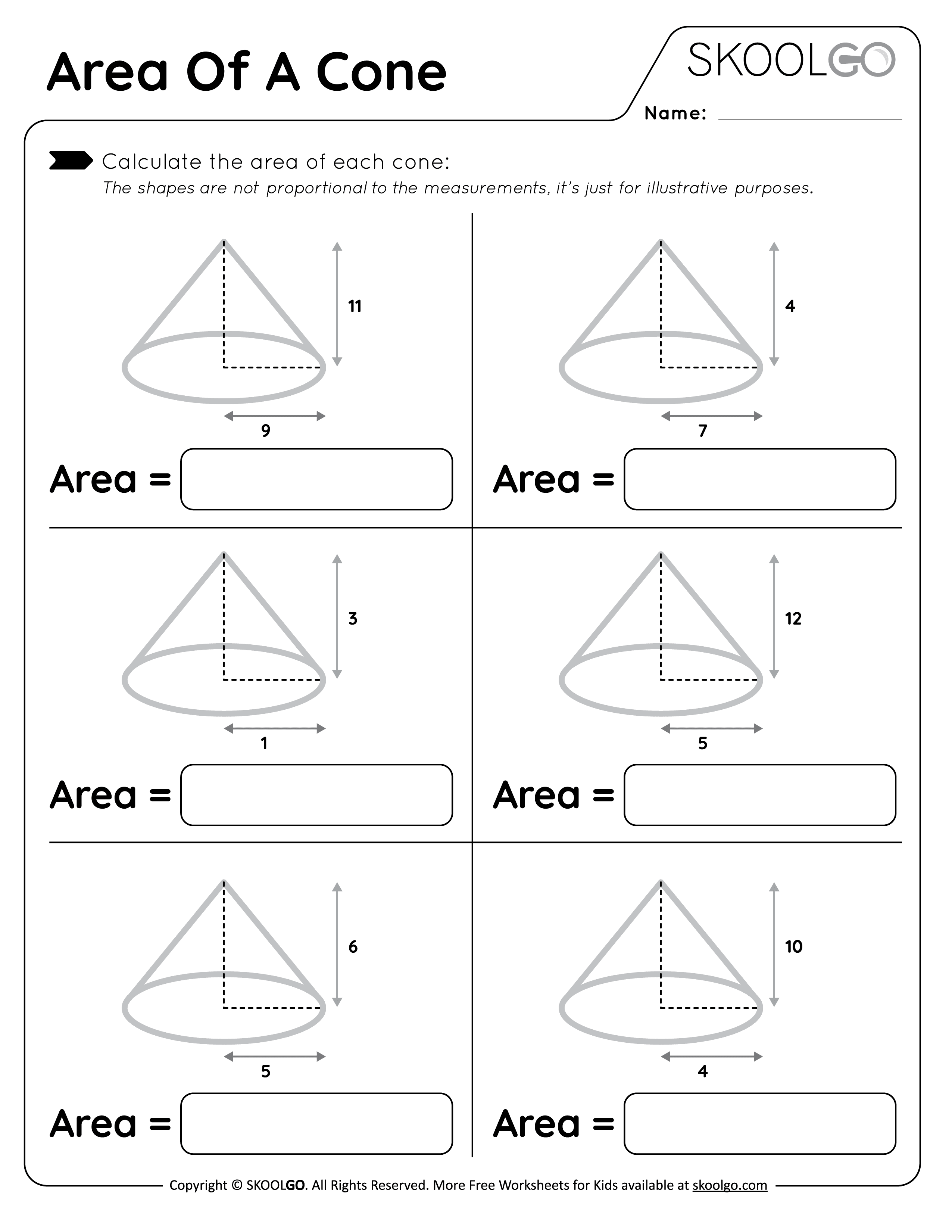
Surface Area of a Rectangular Prism
A rectangular prism has three pairs of equal faces:
| Dimensions | Formula |
|---|---|
| Length (L), Width (W), Height (H) | A = 2LW + 2LH + 2WH |
Follow these steps:
- Calculate the area of each pair of opposite faces.
- Add the areas of all six faces together.
Surface Area of a Cylinder

The cylinder's surface area involves calculating the area of the two circular bases plus the lateral (or curved) surface.
| Dimensions | Formula |
|---|---|
| Radius (r), Height (h) | A = 2πr2 + 2πrh |
Here's the method:
- Calculate the area of the two circular bases.
- Use the circumference of one base to find the lateral surface area.
- Sum up the areas.
📐 Note: Cylinders with bases of varying sizes (truncated cones) use a more complex formula not covered here.
Surface Area of a Sphere
Spheres are the most symmetrical of the common geometric shapes:
| Radius | Formula |
|---|---|
| Radius (r) | A = 4πr2 |
Steps to find the surface area:
- Square the radius of the sphere.
- Multiply by 4π to get the total surface area.
Final Thoughts

Having the right surface area worksheet answers at hand not only helps in checking your work but also in understanding the principles of geometry. By applying the formulas and following the steps for each shape, you can ensure accuracy and develop a deeper comprehension of how these geometric principles apply to real-world objects. Whether for educational purposes or personal interest, mastering surface area calculations is a valuable mathematical skill.
What is the difference between surface area and volume?
+
Surface area measures the total area of the exterior surfaces of an object, while volume measures the space that the object occupies inside its boundaries. Essentially, surface area is about the outside, and volume is about the inside.
Why do we use π in calculating the surface area of cylinders and spheres?
+
The constant π (pi) represents the ratio of a circle’s circumference to its diameter. Since circles are integral to the structure of both cylinders and spheres, π plays a crucial role in their surface area calculations.
How can I remember the formulas for surface area?

+
Practice is key, but mnemonic devices can also help. For example, for a sphere, “4πr²” can be remembered with “Four times pi and radius squared.” For a rectangular prism, think of “Length, Width, Height - Two each to multiply.”