Triangular Prism Surface Area Practice Worksheet for Geometry Students
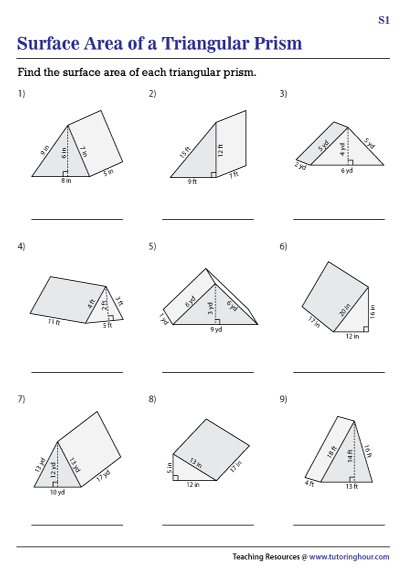
When we delve into the world of geometry, shapes and their properties become an essential part of our understanding. Among the myriad of geometric figures, the triangular prism holds a unique position due to its symmetrical and practical nature. Today, we'll explore an in-depth practice worksheet designed to enhance your skills in calculating the surface area of a triangular prism. Whether you're a student looking to solidify your understanding or a teacher aiming to enrich your lesson plans, this post will guide you through every aspect of this geometric challenge.
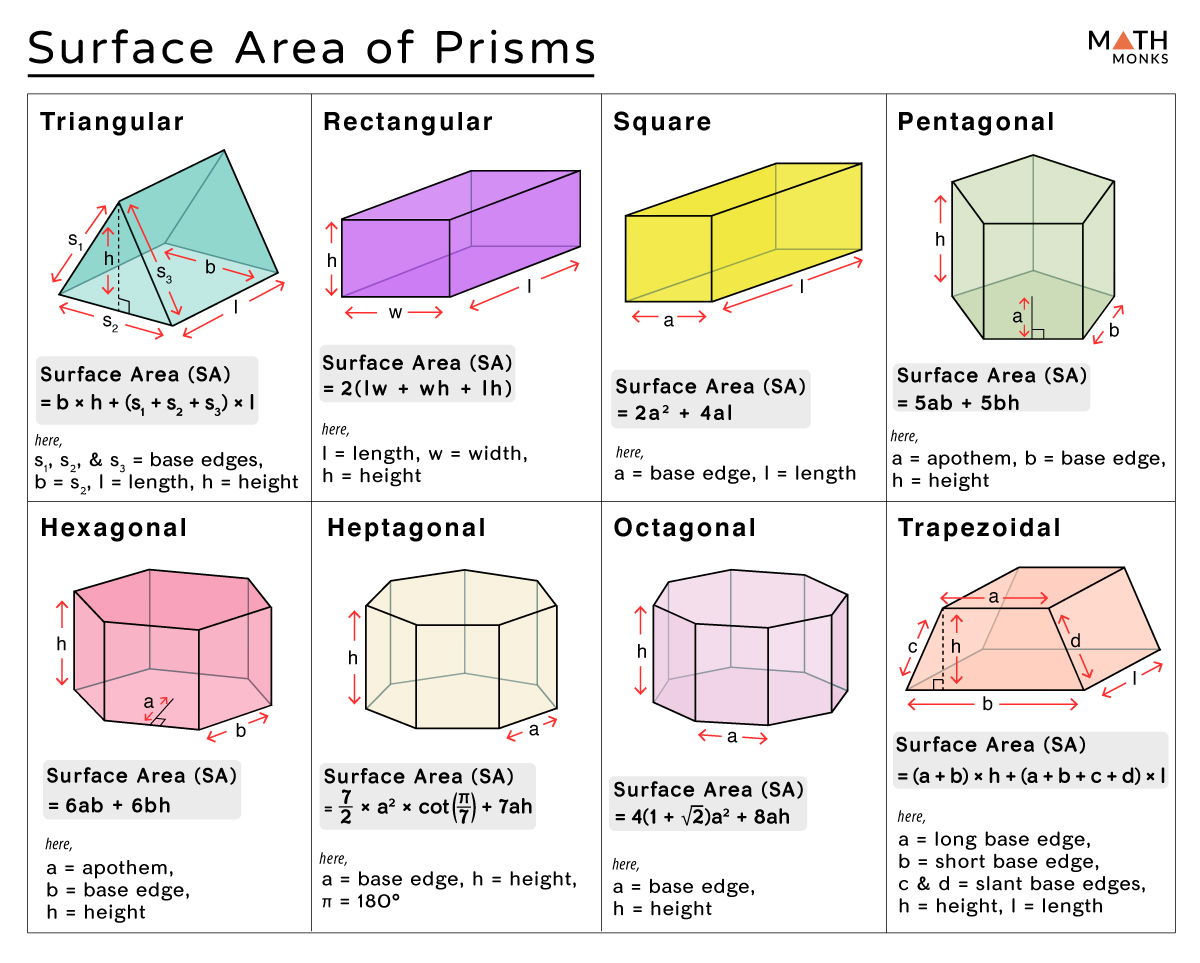
Understanding the Triangular Prism

Before we jump into the practice, it's pivotal to understand what a triangular prism is:
- A triangular prism is a polyhedron made up of two triangular bases and three rectangular lateral faces.
- The bases are congruent, meaning they are identical in shape and size.
- Each vertex of one base is connected to the corresponding vertex of the other base by an edge, creating the prism's sides.
Components of a Triangular Prism
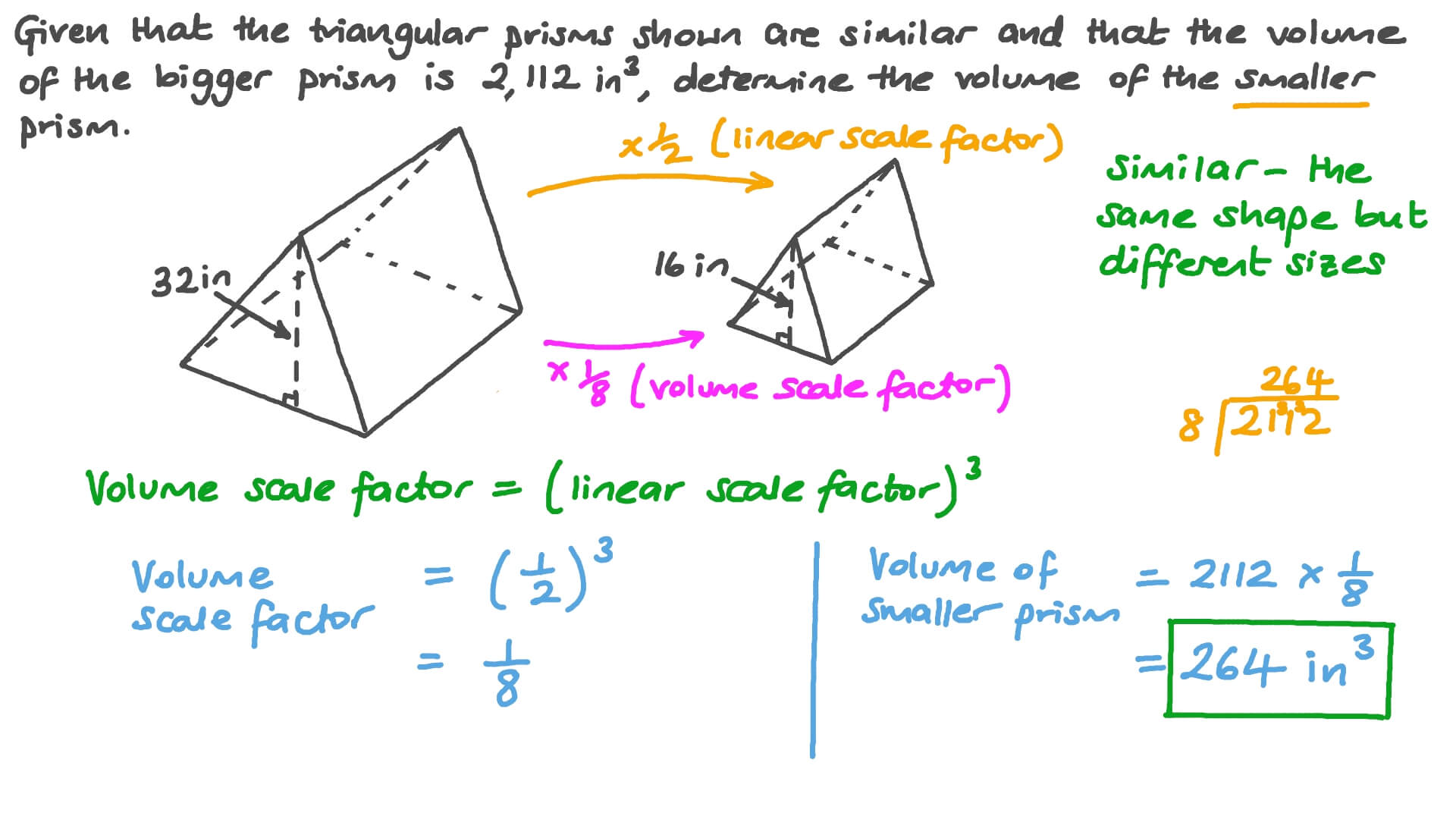
Here are the key components you'll need to know for calculating the surface area:
- Base area: The area of one of the triangular bases.
- Lateral area: The sum of the areas of the three rectangular sides.
- Surface area: The total area of all faces combined.
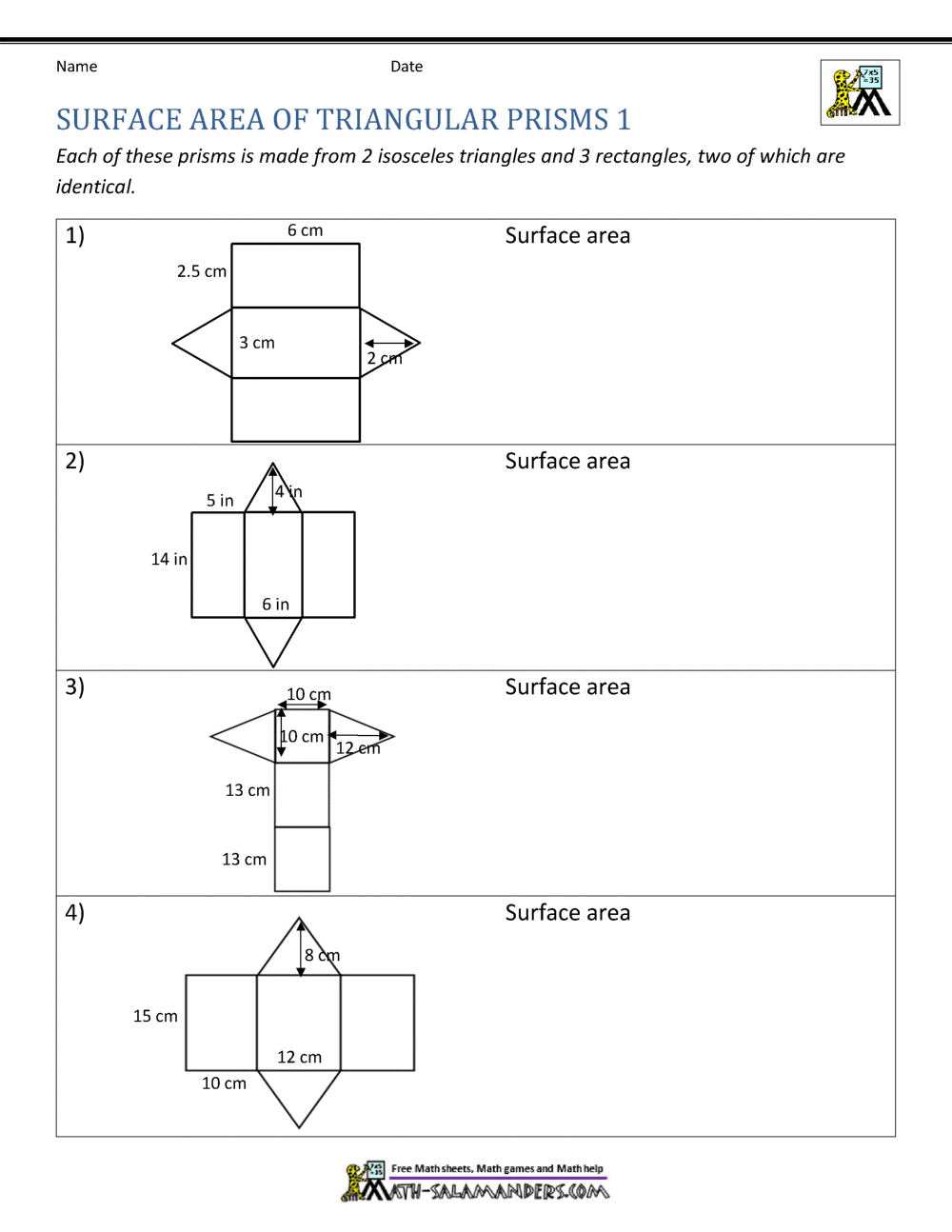
How to Calculate the Surface Area of a Triangular Prism

The formula for calculating the surface area of a triangular prism involves adding the areas of all its faces:
| Part of Prism | Formula |
|---|---|
| Base Area | Base Area = 1/2 × base × height |
| Each Lateral Rectangle | Lateral Rectangle Area = base of triangle × height of prism |
| Total Surface Area | Surface Area = 2 × Base Area + 3 × Lateral Rectangle Area |
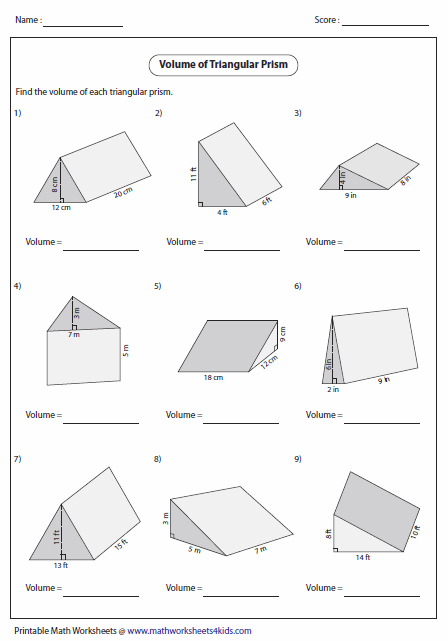
Steps for Calculation

Here's how to approach calculating the surface area:
- Calculate the base area: Use the formula 1/2 × base × height of the triangular base.
- Determine the lateral areas: Each side of the triangle corresponds to one of the heights of a lateral rectangle; multiply this by the height of the prism to get each rectangle's area.
- Sum all areas: Add up the two base areas and the areas of the three lateral rectangles to get the total surface area.
⚠️ Note: Always measure units consistently. Use centimeters, meters, or any other unit throughout the calculations.
Practice Worksheet: Calculating Surface Area

Let's work through some practice problems to master the surface area calculation:
Problem 1: Simple Triangular Prism

Consider a triangular prism with:
- Base edges of length 3 cm, 4 cm, and 5 cm (isosceles triangle).
- Height of the prism is 6 cm.
Calculate the surface area.
Problem 2: Scalene Based Prism

Consider a triangular prism with:
- Base edges of length 2.5 cm, 3.5 cm, and 4 cm (scalene triangle).
- Height of the prism is 7 cm.
Calculate the surface area.
Problem 3: Complex Triangular Prism

Consider a triangular prism with:
- Base edges of length 6 cm, 8 cm, and 10 cm (right angled triangle).
- Height of the prism is 5 cm.
Calculate the surface area.
🔍 Note: For the base area of a right-angled triangle, you can use half of the base times height, or directly use the sides to calculate using Pythagoras theorem.
Tips for Efficient Calculations
- Utilize online calculators or software to check your work, but understand the manual process.
- Sketch your prism to visualize dimensions better.
- Remember, for isosceles and equilateral triangles, symmetry can help in calculations.
- When dealing with right triangles, the legs are often the dimensions given, making base area calculation straightforward.
Having mastered the basics, let's wrap up with some concluding thoughts on mastering the triangular prism's surface area.
Why is it important to understand triangular prism surface area?

+
Understanding triangular prisms and their surface areas can be crucial in various fields such as architecture, engineering, and design, where volume and surface area calculations are critical for material estimates, design specifications, and structural analysis.
Can you find the surface area of a triangular prism with only the base length?

+
No, to calculate the surface area, you need to know the height of the prism and the height of the triangular base as well, because these dimensions determine the area of both the triangular bases and the lateral rectangles.
What happens if the triangular prism is not right-angled?
+
While the calculation steps remain the same, you must be careful to find the correct height of the base triangle, which might not align with one of its sides. You could use trigonometry or geometric properties to find this height if not given directly.
In closing, mastering the surface area calculation of triangular prisms not only enhances your problem-solving skills but also opens doors to understanding more complex geometric concepts. By practicing these problems, you’ve taken a significant step towards geometric proficiency. Remember, geometry is as much about visualization and spatial reasoning as it is about numbers. Keep practicing, and let each prism calculation reinforce your confidence and competence in this fascinating subject.