5 Tips for Mastering Surface Area of Square Pyramids

In the realm of mathematics, understanding the surface area of three-dimensional shapes can be both fascinating and practically useful. Square pyramids, with their distinct geometric form, are excellent examples to explore when honing your geometric calculation skills. Let's delve into five invaluable tips for mastering the calculation of the surface area of square pyramids:
1. Understand the Components
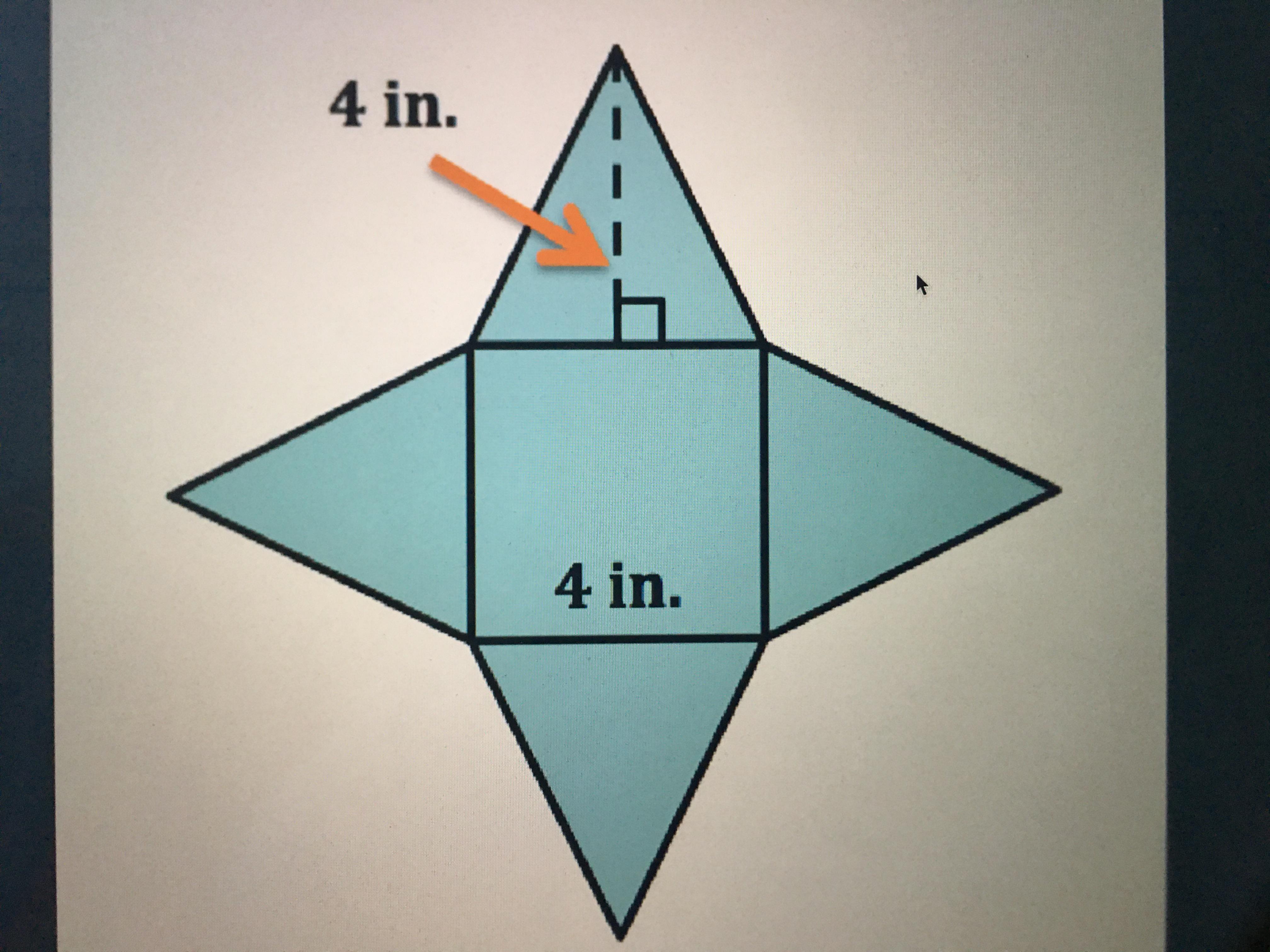
A square pyramid is composed of one square base and four triangular faces. Here’s how you can break it down:
- Base: A square with side length ’s’.
- Triangular Faces: Each triangular face has its base as ’s’ and its height extending from the center of the base to the apex of the pyramid, called the slant height ‘l’.

📌 Note: The slant height ‘l’ can be calculated using Pythagorean theorem, knowing the altitude and the distance from the center of the base to one of its sides.
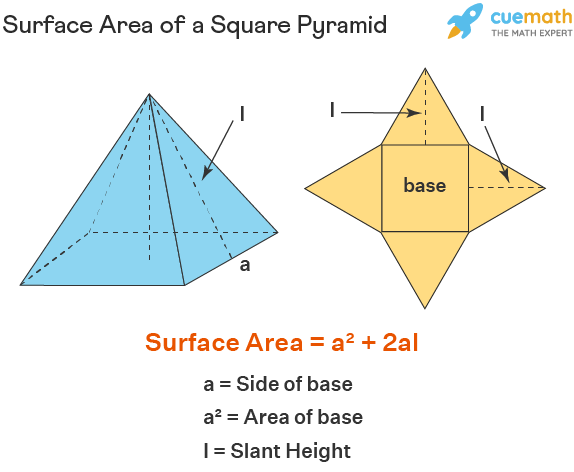
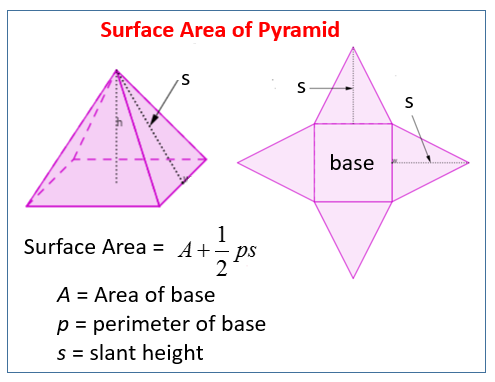
2. Formula for Surface Area

The surface area of a square pyramid (A) can be found with the formula:
| Part of Pyramid | Formula |
|---|---|
| Base Area | s2 |
| Triangular Faces Area | 0.5 * s * l * 4 |

This results in:
[ A = s^2 + 2s \cdot l ]3. Accurate Measurement is Key

Ensure your measurements are precise because even small errors can lead to significant discrepancies:
- Side Length: Use a ruler or tape measure for the side of the base.
- Slant Height: This can be measured directly or calculated from known dimensions.
📌 Note: Always verify your measurements twice, as geometric figures are sensitive to accuracy.
4. Utilize Visualization Tools
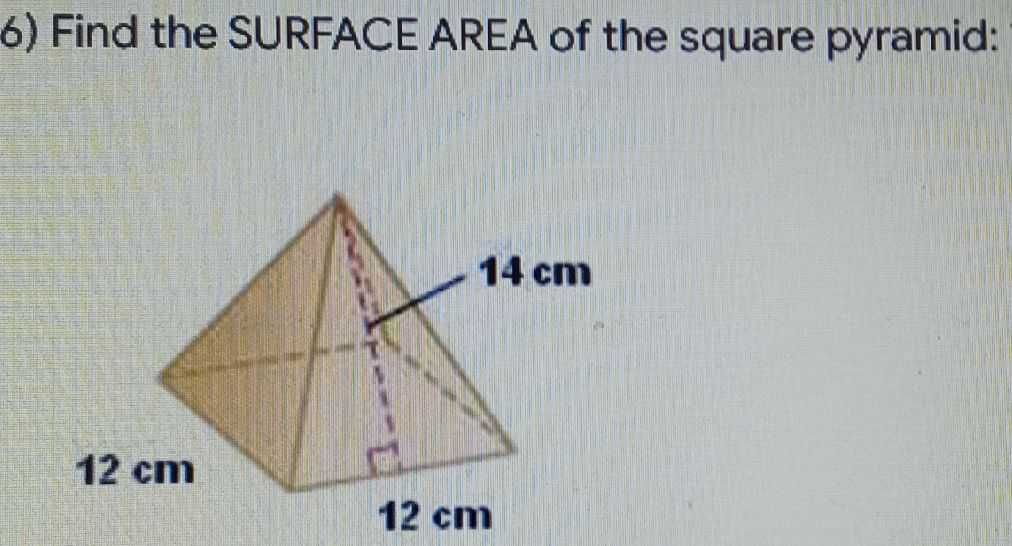
Visual aids can significantly help in understanding and calculating surface area:
- Use drawing tools like graph paper to sketch the pyramid.
- 3D modeling software can provide dynamic views of the pyramid, enhancing your comprehension of its geometry.

5. Practice with Real-World Examples

Apply your knowledge to real-world scenarios where square pyramids are common:
- Roofs and Architecture: Many modern buildings feature pyramid-like roofs.
- Pyramids and Ziggurats: Calculate the surface area of historical structures.
Here’s how you might approach a real-world example:
- Determine the dimensions from blueprints or measurements.
- Use the formula to find the total surface area.
- Consider additional factors like material cost or volume.
To sum up, mastering the surface area of square pyramids involves a blend of understanding the geometry, precise measurement, leveraging visualization, and applying this knowledge to real-life scenarios. Each of these steps not only builds mathematical proficiency but also fosters a deeper appreciation for the architectural and mathematical elegance of these structures. Whether you're studying for an exam, designing a structure, or just satisfying your curiosity about geometry, these tips will serve as your guide to calculate with confidence.
Why is it important to calculate the surface area of a pyramid?
+
The calculation of surface area is critical for understanding how much material is needed to cover the structure or how much paint or sealant is required. It’s also vital for understanding heat dissipation, thermal dynamics, and can be used in educational settings to illustrate volume and surface relationships.
Can I calculate the slant height without knowing the altitude?

+
If you know the side length of the base and the slant height isn’t measured, you can use the Pythagorean theorem, where the altitude forms one leg, and half the diagonal of the base is the other leg. Alternatively, if you have the volume or some other dimensions, you might infer the slant height.
What if the base of my pyramid isn’t square?
+
For a non-square pyramid (like a rectangular pyramid), the calculation becomes a bit more complex. You’d calculate the area of the rectangular base and add the area of each triangular face separately, taking into account different slant heights or bases for each face if they’re not identical.
Can I use trigonometry to calculate the surface area?
+
Yes, trigonometry can be used to find the slant height if you have the altitude and the radius of the inscribed circle in the base. Once the slant height is known, you can proceed with regular surface area calculations.