Mastering Triangular Prism Surface Area: Worksheet Guide

Introduction to Triangular Prism Surface Area

Understanding the surface area of a triangular prism can be both an educational and practical skill. Triangular prisms are three-dimensional shapes that consist of two triangular bases and three rectangular sides, making them unique in geometry. This blog post will guide you through how to calculate the surface area of a triangular prism using a dedicated worksheet approach.
Why Learn Triangular Prism Surface Area?

Knowing the surface area of any geometrical shape is beneficial:
- Packaging and Design: It helps in understanding how much material is needed for packaging.
- Architecture: Architectural designs often require these calculations for material estimates.
- Education: It’s an essential topic in geometry and solidifies spatial understanding.
Understanding the Triangular Prism

Before diving into calculations, it’s crucial to understand the structure of a triangular prism:
- Two triangular bases which are congruent.
- Three rectangular faces, each joining corresponding sides of the triangular bases.
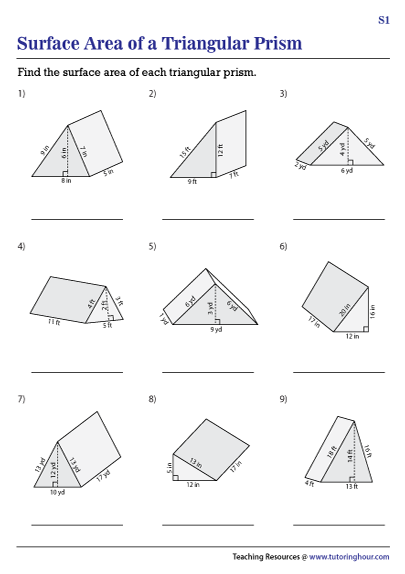
Here is an image of what a triangular prism looks like:

Worksheet for Calculating Surface Area

Here’s how you can use a worksheet to calculate the surface area of a triangular prism:
| Step | Description |
|---|---|
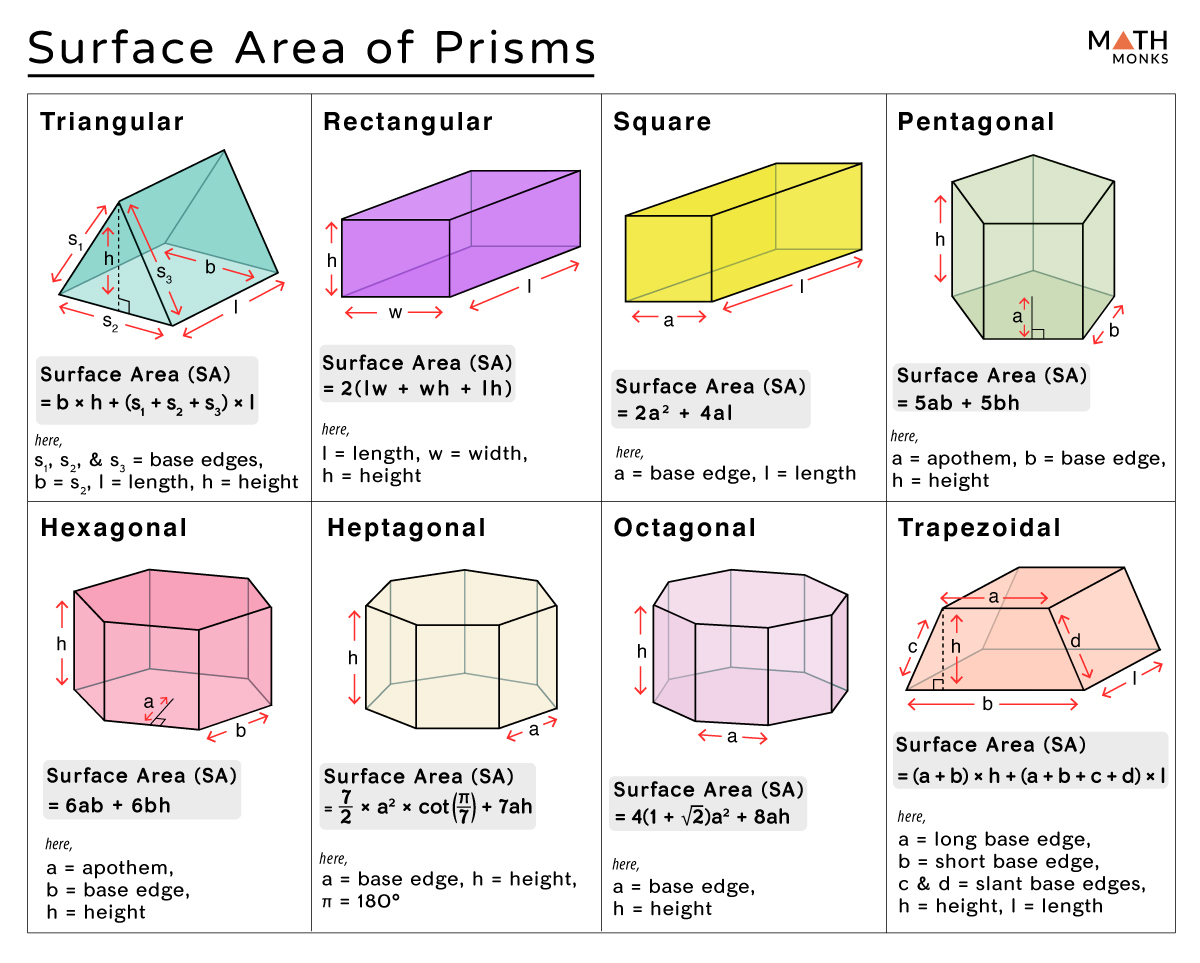
| 1. | Identify the dimensions of your prism: |
|
|
| 2. | Calculate the area of one triangular base: Area of triangle = (base * height of triangle) / 2 |
| 3. | Multiply by 2 to account for both bases. |
| 4. | Find the perimeter of one triangular base: Perimeter = side1 + side2 + side3 |
| 5. | Calculate the area of one rectangular face: Area of rectangular face = Perimeter * Height of Prism |
| 6. | Add all areas: Total Surface Area = 2 * Area of one triangular base + Area of one rectangular face * 3 |
🔖 Note: Ensure all measurements are in the same unit to get an accurate result.
Practical Application of Surface Area
Once you master the calculation of a triangular prism’s surface area, here are some practical applications:
- Construction: Estimating material like roofing or siding for triangular structures.
- Manufacturing: Designing and cutting materials for boxes or packaging.
- Art: Creating geometric art or sculptures where precision in surface area is needed.
Key Points for Mastery

To truly master the concept:
- Understand each step in the calculation process.
- Practice with real-world objects, like a tent or a roof.
- Explore 3D modeling software to visualize the shapes and calculations.
In summary, learning to calculate the surface area of a triangular prism not only enhances your understanding of geometry but also provides you with practical skills applicable in numerous fields. By following the steps outlined in this worksheet guide, you can become proficient in estimating materials, designing, and even in artistic endeavors where geometry plays a crucial role. Whether you're a student, an architect, or an enthusiast of mathematics, mastering this concept will undoubtedly serve as a valuable tool in your intellectual toolkit.
What is the difference between surface area and volume?

+
Surface area measures the total area of the outer surfaces of a shape, while volume measures the amount of space it occupies.
Can the formula for surface area change?

+
Yes, the formula might change slightly based on the specific dimensions provided. For example, if the triangular bases are isosceles, right, or equilateral, the calculation might differ slightly due to symmetry or special properties.
What are common mistakes when calculating surface area?

+
Common mistakes include:
- Using different units for measurements.
- Forgetting to multiply by 2 for the area of both triangular bases.
- Incorrectly calculating the perimeter or base area due to misunderstandings of the shape’s geometry.