5 Steps to Solve Triangular Prism Surface Area

Solving for the surface area of a triangular prism can seem daunting if you're new to geometry, but breaking it down into steps makes the process straightforward and manageable. Here's how you can master this skill:
Step 1: Understand the Triangular Prism

A triangular prism has six faces. Here’s how you can understand its structure:
- 2 triangular bases: These are congruent and form the top and bottom of the prism.
- 3 rectangular lateral faces: These join the corresponding sides of the triangular bases.

Step 2: Measure and Calculate the Area of Triangular Bases
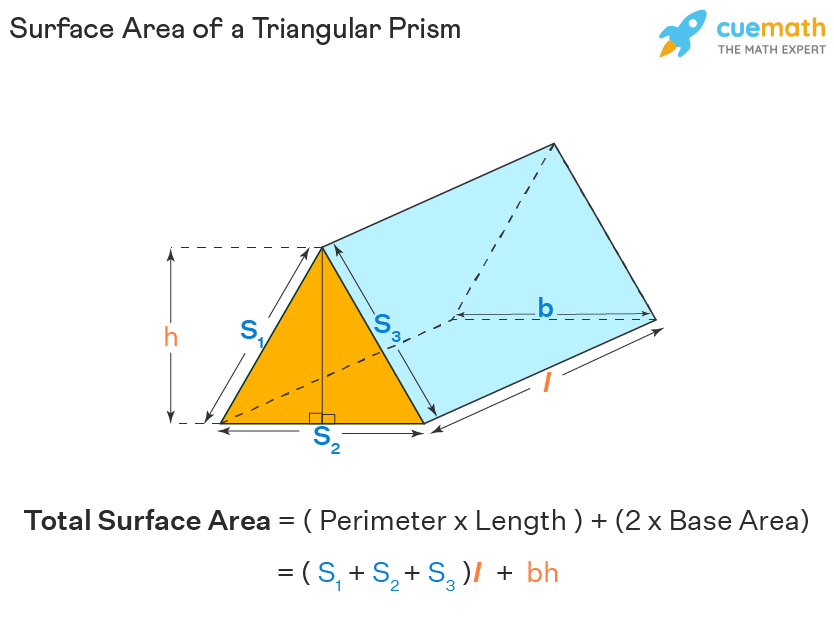
The first step is to calculate the area of the triangular bases:
- Determine the base (b) and height (h) of one triangle.
- Use the formula:
Area = 0.5 * base * height - Calculate this for one triangle and then double it since there are two bases.
📏 Note: Ensure your measurements are accurate as small errors can significantly impact the final surface area.
Step 3: Find the Perimeter of One Triangular Base
Next, find the perimeter of one of the triangular bases:
- Sum the lengths of all three sides of one triangle.
Step 4: Calculate the Area of the Rectangular Faces

Now, for each lateral face:
- Multiply the length of the corresponding side of the triangle by the height of the prism (L).
- Do this for each side of the triangle, resulting in three rectangles.
Here is a simple calculation table:
| Side of Triangle | Height of Prism (L) | Area of Rectangle |
|---|---|---|
| A | L | A * L |
| B | L | B * L |
| C | L | C * L |

Step 5: Sum All Areas

Finally, add all the areas together:
- Add the area of the two triangular bases.
- Add the sum of all the rectangular face areas.
By following these steps, you've computed the total surface area of the triangular prism.
This method provides a clear framework for calculating surface areas, which is useful in real-world applications like designing prismatic structures or understanding volume and surface interactions in engineering and architecture.
Why are the triangular bases of a prism congruent?

+
Congruent bases ensure the prism is uniform along its length, making calculations and construction simpler.
Can the height of the triangular bases be the same as the height of the prism?

+
Generally no. The height of the prism refers to the distance between the parallel bases, whereas the height of the triangles relates to their own perpendicular height.
How do I calculate the perimeter of an irregular triangle?

+
You measure each side individually and sum these lengths to find the perimeter.



