Surface Area of Solids: Master Geometry Now!

Mastering the concept of surface area in geometry is not just an academic endeavor but a practical skill that finds applications in various fields, from architecture to engineering. Whether you're dealing with everyday objects or complex structures, understanding how to calculate the total surface area of different solids is crucial. In this comprehensive guide, we'll delve into the formulas, techniques, and practical applications of calculating surface area for a range of geometric shapes, ensuring you become adept at this fundamental aspect of geometry.
What is Surface Area?

Before we dive into the specifics, let’s clarify what we mean by surface area. The surface area of a solid is the sum of the areas of all its faces or surfaces. For simple shapes like a cube or rectangular prism, this might be straightforward, but for more complex figures like cones or spheres, additional steps are required. Surface area calculation is not just about solving math problems; it’s essential for:
- Determining the amount of material needed for packaging or construction.
- Calculating paint required to cover an object.
- Analyzing heat transfer in engineering designs.
- Estimating the cost and resources for a project.
Common Solids and Their Surface Area Formulas

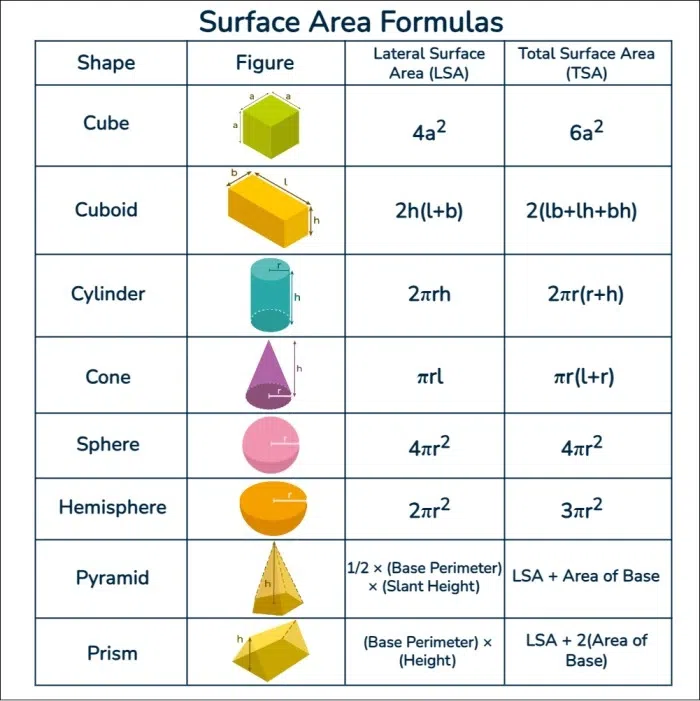
Cube

A cube, with all sides of equal length, is perhaps the simplest solid. Here’s how to calculate its surface area:
- Formula:
Surface Area = 6s², where s is the side length. - Calculation Example: If a cube has a side length of 5 units, its surface area is
6 × 5² = 6 × 25 = 150 square units.
Rectangular Prism

Often referred to as a cuboid, this shape has different edge lengths. Its surface area formula is:
- Formula:
Surface Area = 2(lw + lh + wh), where l is length, w is width, and h is height. - Calculation Example: For a rectangular prism with dimensions 4 units, 3 units, and 5 units, the surface area would be
2 × (4 × 3 + 4 × 5 + 3 × 5) = 2 × (12 + 20 + 15) = 2 × 47 = 94 square units.
Cylinder

A cylinder has two circular bases and a curved surface. Here’s how you calculate its surface area:
- Formula:
- Total Surface Area = 2πr² + 2πrh, where r is the radius and h is the height.
- Lateral Surface Area (only the side) = 2πrh.
- Calculation Example: For a cylinder with radius 3 units and height 10 units, the total surface area would be
2 × π × 3² + 2 × π × 3 × 10 ≈ 113.1 square units(using π ≈ 3.14).
Sphere

The surface area of a sphere is:
- Formula:
Surface Area = 4πr², where r is the radius. - Calculation Example: For a sphere with a radius of 7 units, its surface area is
4 × π × 7² ≈ 615.8 square units.
Cone

The surface area of a cone includes both the circular base and the lateral surface:
- Formula:
- Total Surface Area = πr² + πrl, where r is the radius of the base, l is the slant height.
- Lateral Surface Area = πrl.
- Calculation Example: Given a cone with a base radius of 5 units, slant height of 13 units, and height of 12 units, the total surface area is
π × 5² + π × 5 × 13 ≈ 204.2 square units.
Practical Applications and Advanced Techniques

Calculating surface area isn’t just about plugging numbers into formulas. Here are some practical applications and tips:
- Engineering and Architecture: Understanding surface area helps in material estimation, structural design, and thermal performance analysis.
- Packaging: Knowledge of surface area is essential for efficient packaging design, reducing material waste.
- 3D Printing: Surface area calculation can determine print time and material consumption for 3D printed objects.
- Fluid Dynamics: In fluid dynamics, surface area influences drag and lift forces on objects like airplanes or cars.
Techniques for Complex Shapes

When dealing with irregular or complex shapes:
- Approximate using simpler shapes (e.g., breaking a pyramid into triangular prisms).
- Use software tools like CAD for precise surface area calculations.
- Consider differential geometry for organic shapes or surfaces with varying curvature.
📝 Note: For shapes where exact calculations are challenging, calculus or approximation methods can be employed to estimate surface areas with high accuracy.
Recap and Final Thoughts

As we’ve journeyed through the world of surface area calculations, it’s clear that this skill transcends mere mathematical problem-solving. From practical applications in everyday life to advanced applications in engineering, architecture, and beyond, mastering surface area calculation has tangible benefits. We’ve explored:
- The basic concepts and importance of surface area.
- Formulas for common geometric solids.
- Real-world applications where surface area plays a critical role.
- Advanced techniques for calculating the surface area of complex shapes.
Keep in mind, continuous practice and exploring different shapes will enhance your proficiency in calculating surface areas, making geometry not just an academic subject but a tool for problem-solving in real-life scenarios.
What is the difference between surface area and volume?

+
Surface area refers to the sum of all the areas of a solid’s external faces, while volume measures the space it occupies inside. Surface area deals with the exterior, whereas volume deals with the interior.
Can surface area be calculated for any shape?

+
Yes, but the complexity can vary. For simple geometric solids, there are straightforward formulas. For irregular or complex shapes, you might need to approximate, use calculus, or rely on software to calculate surface area accurately.
How does surface area affect real-world applications?
+
Surface area impacts various factors like material costs, structural integrity, heat transfer, and even biological processes in living organisms. For example, in packaging, minimizing surface area reduces material usage, thus saving costs.