Rectangular Pyramid Surface Area: Fun Worksheet Guide

Geometry often presents a variety of shapes that challenge us to think in three dimensions, and one of the more intriguing shapes is the rectangular pyramid. Often overlooked in favor of its more famous cousin, the triangular pyramid or tetrahedron, the rectangular pyramid offers unique challenges and opportunities for education. This guide will not only provide a fun worksheet but also delve into how to calculate the surface area of a rectangular pyramid, complete with practical examples, step-by-step instructions, and educational tips for enhancing your understanding.
Understanding Rectangular Pyramids

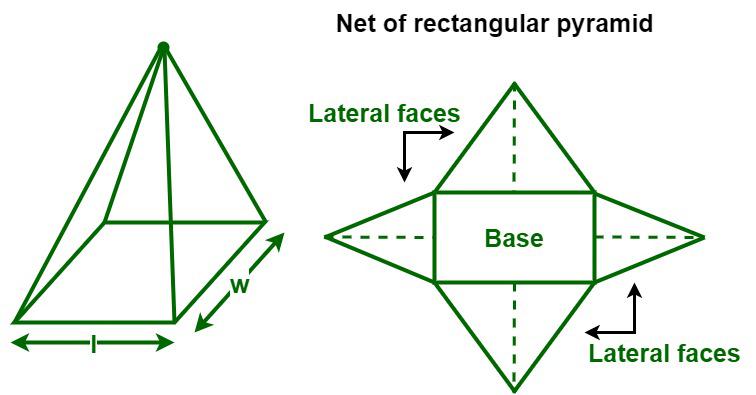
What is a Rectangular Pyramid? A rectangular pyramid is a pyramid with a rectangular base and four triangular faces meeting at a single apex. Here’s a quick visual aid to get you started:

The Parts of a Rectangular Pyramid

- Base: A rectangle with sides length a and b.
- Triangular Faces: Each face has sides of lengths a, b, and s where s is the slant height, which is the distance from the apex to the midpoint of a base edge.
- Apex: The common vertex where all triangular faces meet.
- Edges: The sides of the pyramid, including the base edges (4 in total) and the edges from the apex to the vertices of the base (4 in total).
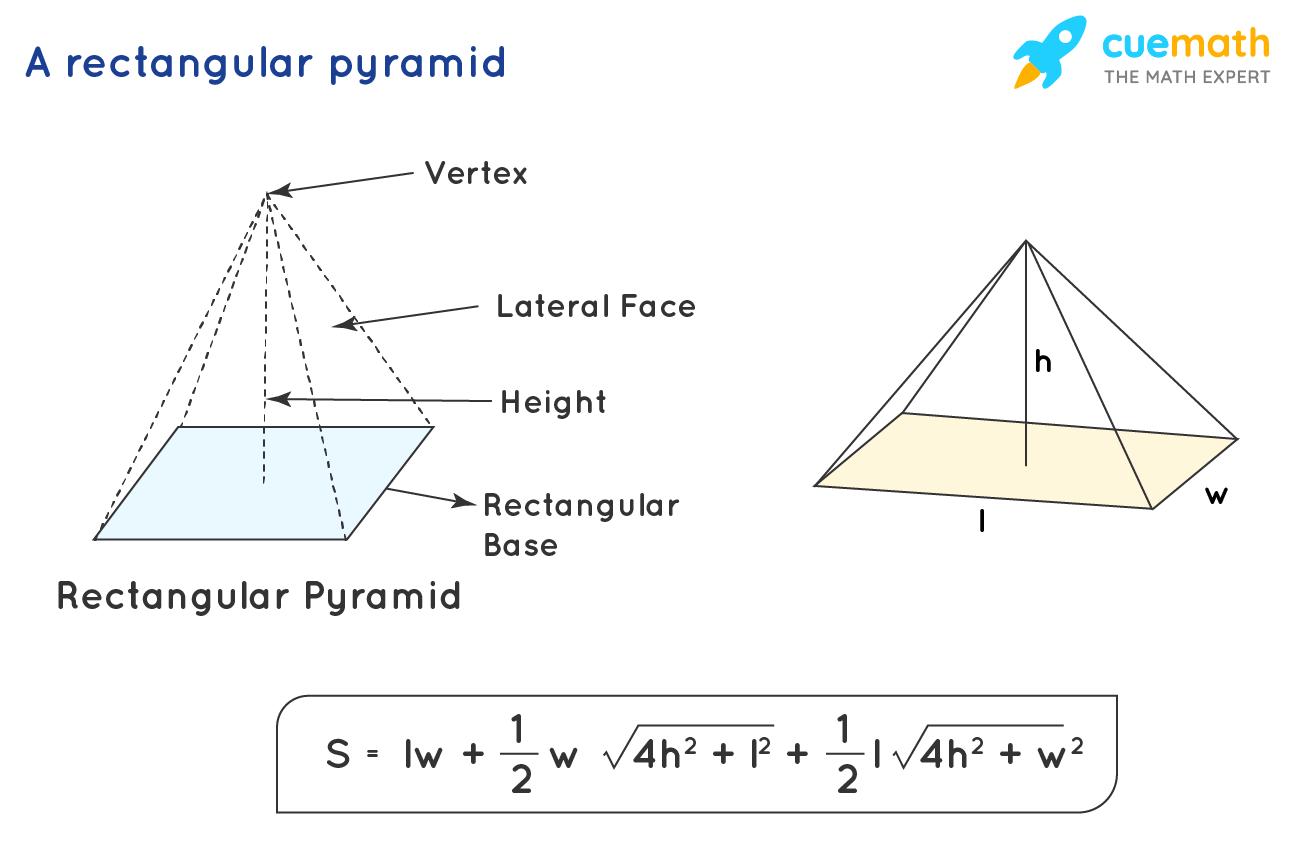
Calculating the Surface Area

The surface area of a rectangular pyramid consists of:
- The area of the base.
- The sum of the areas of the four triangular faces.
Formula for Surface Area

The formula to calculate the surface area (A) of a rectangular pyramid is:
[ A = ab + \frac{1}{2} \times p \times s ]
Where:
- a and b are the lengths of the sides of the base.
- p is the perimeter of the base (2a + 2b).
- s is the slant height.
Example Calculation
Let’s say we have a pyramid with a base 5 units by 6 units, and a slant height of 4 units:
- Base Area: 5 * 6 = 30 square units
- Perimeter: 2(5 + 6) = 22 units
- Surface Area: 30 + 0.5 * 22 * 4 = 61 square units
Fun Worksheet Guide
Here’s how you can use a worksheet to engage students or anyone interested in learning about rectangular pyramids:
Step-by-Step Guide:

- Introduction: Begin with a brief overview of what a rectangular pyramid is and its parts.
- Problem Set: Provide problems where students must calculate the surface area given the base dimensions and the slant height.
- Visual Aids: Include diagrams of pyramids with labeled dimensions to help with visualization.
- Practical Examples: Incorporate real-life applications, like architecture or packaging, to make the topic relatable.
- Worksheet Structure:
Problem Base Dimensions Slant Height Surface Area 1 5m x 6m 4m ? 2 8ft x 10ft 7ft ? 
- Answer Key: An answer key at the end for students to check their work.
✏️ Note: Encourage students to draw their pyramids on grid paper to better visualize the problem.
Wrapping it up

Understanding how to calculate the surface area of a rectangular pyramid not only expands our geometric knowledge but also has practical applications in fields like architecture, civil engineering, and even in everyday tasks like calculating material for a DIY project. The fun worksheet provided here serves as an engaging tool for learning and applying these concepts, promoting both educational growth and enjoyment in math.
What is the difference between surface area and volume?

+
The surface area of a shape refers to the total area that covers the outside of it, whereas volume refers to the amount of space that a three-dimensional object occupies. In a rectangular pyramid, we calculate surface area by summing the areas of all faces, while volume involves the space inside the pyramid.
Can you calculate the surface area if only the base dimensions are known?

+
No, you need the slant height to accurately calculate the surface area of the triangular faces of a rectangular pyramid. However, you can calculate the area of the base alone.
How does the slant height affect the surface area?

+
The slant height directly influences the area of the triangular faces. A greater slant height results in larger triangular faces, thus increasing the overall surface area.



