5 Tips to Master Rectangular Prism Surface Area

Embarking on a journey through geometry can be both enlightening and challenging, especially when it comes to understanding the intricacies of three-dimensional shapes. One such shape is the rectangular prism—a common and highly applicable figure that finds its uses in diverse fields like architecture, packaging, and engineering. Calculating the surface area of a rectangular prism is a fundamental skill for those dealing with space and volume, and here we present a comprehensive guide to help you master this concept.
The Basics: Understanding the Rectangular Prism


Before delving into the methods for calculating surface area, let’s define what we’re working with. A rectangular prism is a polyhedron with six faces, all of which are rectangles. It has:
- Three pairs of congruent, parallel faces
- Eight vertices
- Twelve edges
The surface area of a rectangular prism is the total area of all its faces. This is critical for practical applications like estimating material for construction, packaging design, or understanding the space an object will occupy.
Tip 1: Identify the Measurements
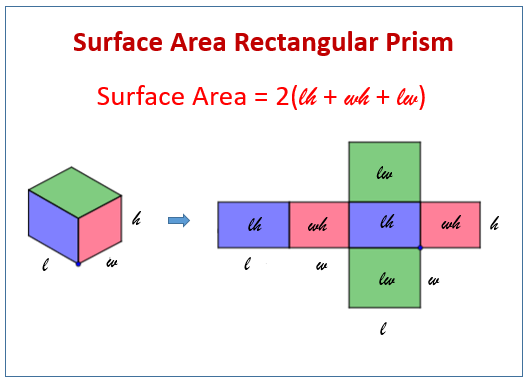
To start, you’ll need to know:
- Length (l)
- Width (w)
- Height (h)
These are the dimensions along the three axes of the rectangular prism.
Tip 2: Use the Surface Area Formula

The formula for the surface area (SA) of a rectangular prism is:
SA = 2lw + 2lh + 2wh
Where:
- lw is the area of the base
- lh is the area of the sides
- wh is the area of the front and back
Remember to add up all these areas because the total surface area includes both the top and bottom, as well as the four side faces.
🔎 Note: This formula can be remembered easily if you understand that each pair of faces has the same area, hence the multiplication by two.
Tip 3: Break it Down with Visual Aids

| Face | Area | Formula |
|---|---|---|
| Base | lw | Length x Width |
| Top | lw | Length x Width |
| Side 1 | lh | Length x Height |
| Side 2 | lh | Length x Height |
| Front | wh | Width x Height |
| Back | wh | Width x Height |

Visual aids like tables or diagrams help in understanding how the total surface area is calculated from the different faces.
Tip 4: Practice with Examples

Here’s a simple example to cement the concept:
- Length = 6 units
- Width = 5 units
- Height = 4 units
Using the formula:
SA = 2(6 * 5) + 2(6 * 4) + 2(5 * 4)
Let's break it down:
- 2lw = 2(6 * 5) = 60 units²
- 2lh = 2(6 * 4) = 48 units²
- 2wh = 2(5 * 4) = 40 units²
Total Surface Area = 60 + 48 + 40 = 148 units²
Tip 5: Utilize Online Calculators and Interactive Tools

In today’s digital age, numerous online tools exist to calculate surface area:
- Interactive websites and apps that provide visual simulations of changing dimensions.
- Online calculators for immediate surface area calculation.
Utilizing these tools can enhance your understanding of the relationships between the prism's dimensions and its surface area.
🌐 Note: Online tools are great for quick calculations but understanding the underlying math is paramount for real-world applications.
When calculating the surface area of rectangular prisms, remember these tips can significantly improve your proficiency and accuracy. Whether you're a student learning geometry or a professional needing practical application, these guidelines can be invaluable. Practice with real-world examples, utilize digital tools, and always visualize the shape and its components. This holistic approach will not only deepen your understanding but also make the process more enjoyable and less daunting.
Why is understanding the surface area of a rectangular prism important?

+
The surface area informs us about the amount of material needed to cover or construct the prism, which has numerous applications in packaging, design, and construction.
Can you find the surface area without all three dimensions?

+
Without all three dimensions, you cannot compute the entire surface area because each face’s area depends on a unique combination of these dimensions.
How does changing one dimension affect the surface area?
+
Altering one dimension impacts the areas of multiple faces, making the surface area recalculation necessary for an accurate estimation.
What are some common mistakes when calculating surface area?

+
Frequent errors include forgetting to double the areas for paired faces, neglecting units of measurement, or miscalculating the areas of each face.
Are there alternative methods for calculating surface area?

+
While the formula provided is straightforward, you can also sum up the areas of all individual faces directly or use more advanced geometric techniques in certain contexts.