Surface Area Mastery: Rectangular Prism Practice Worksheets

Geometry, a branch of mathematics that deals with the study of shapes, sizes, and the properties of space, often introduces students to calculating the surface area of various shapes as a fundamental skill. Among the shapes commonly explored is the rectangular prism, which, with its straightforward six faces, makes an excellent subject for understanding surface area calculations. This blog post delves into the world of surface areas, focusing particularly on mastering the surface area of rectangular prisms through practice worksheets. Whether you're a student, teacher, or math enthusiast, this comprehensive guide will equip you with the knowledge and tools needed to excel.
The Importance of Surface Area Calculations

Understanding how to calculate the surface area of a rectangular prism is not just an academic exercise; it has numerous practical applications. Here's why it matters:
- Construction: Builders need to know the surface area to calculate material costs for covering surfaces.
- Packaging: Companies use surface area calculations to design packaging that minimizes material use while maximizing space efficiency.
- Engineering: Engineers might calculate the heat dissipation capacity of an object based on its surface area.
- Art and Design: Artists and designers use surface area measurements to plan murals or to create optical illusions on flat surfaces.
Understanding Rectangular Prisms

A rectangular prism, also known as a cuboid, is a three-dimensional shape where all faces are rectangles. Here are the key components you need to understand:
- Length: The longest side of the prism.
- Width: The shortest side adjacent to the length.
- Height: The vertical distance between the top and bottom faces.
Formula for Surface Area of a Rectangular Prism
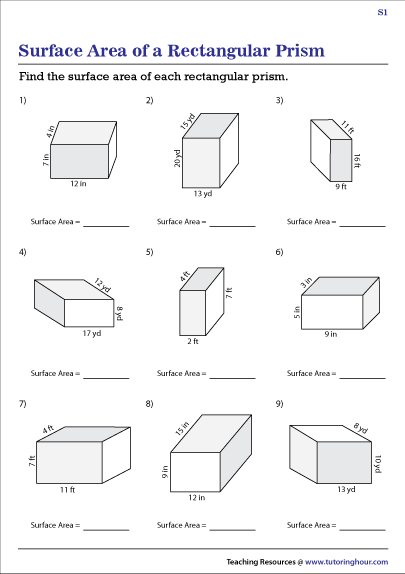
To calculate the total surface area of a rectangular prism, you use the following formula:
- Total Surface Area: SA = 2lw + 2lh + 2wh
Where:
- l = length
- w = width
- h = height
The Process of Calculation

Here are the steps to find the surface area:
- Identify and record the length, width, and height of the prism.
- Calculate the area for each pair of opposite faces:
- Front and Back: lw
- Right and Left: lh
- Top and Bottom: wh
- Add all six face areas together and multiply by two for the total surface area.
Practical Examples
Let's look at some examples to put theory into practice:
Example 1:
A rectangular prism has a length of 5 units, a width of 3 units, and a height of 4 units.
- Front/Back Area: 5 units x 3 units = 15 square units
- Right/Left Area: 5 units x 4 units = 20 square units
- Top/Bottom Area: 3 units x 4 units = 12 square units
- Total Surface Area = 2 x (15 + 20 + 12) = 94 square units
Example 2:
A larger box with dimensions 10 units by 8 units by 6 units.
- Front/Back Area: 10 units x 8 units = 80 square units
- Right/Left Area: 10 units x 6 units = 60 square units
- Top/Bottom Area: 8 units x 6 units = 48 square units
- Total Surface Area = 2 x (80 + 60 + 48) = 376 square units
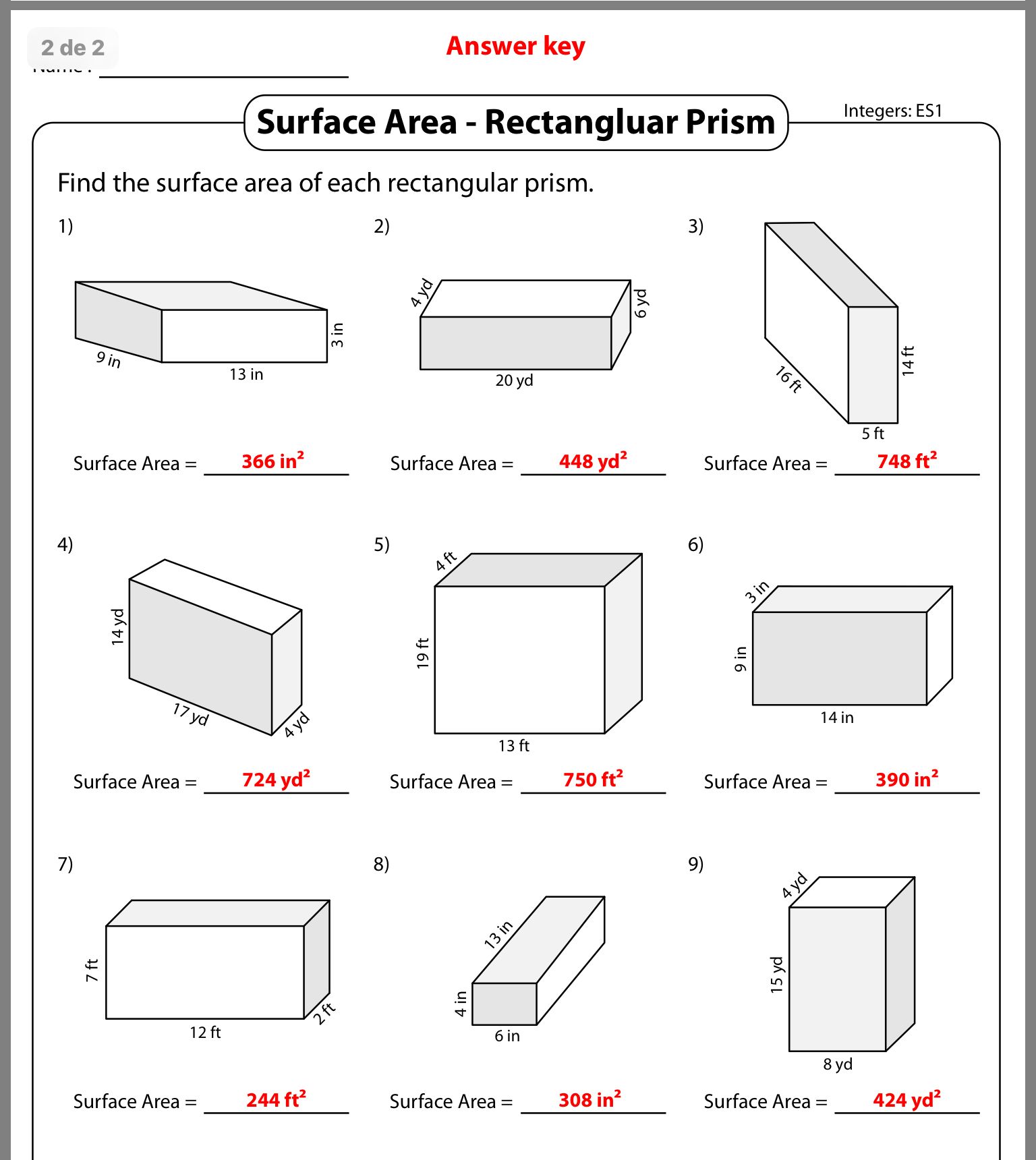
Practice Worksheets
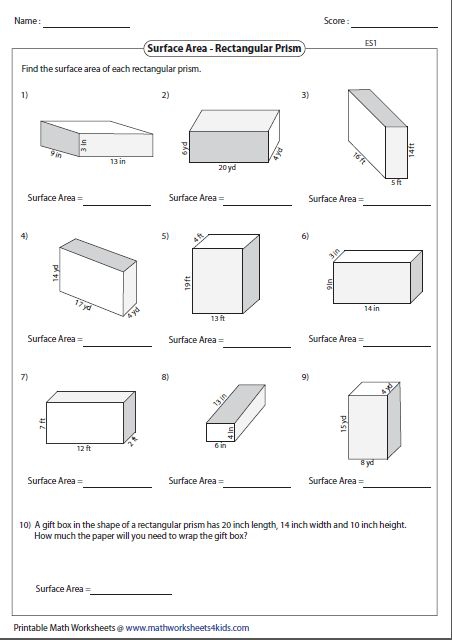
Developing proficiency requires practice. Here's a basic worksheet to start with:
| Length | Width | Height | Total Surface Area |
|---|---|---|---|
| 3 cm | 2 cm | 4 cm | ______ |
| 6 m | 5 m | 2 m | ______ |
| 8 in | 7 in | 3 in | ______ |
| 12 ft | 10 ft | 6 ft | ______ |
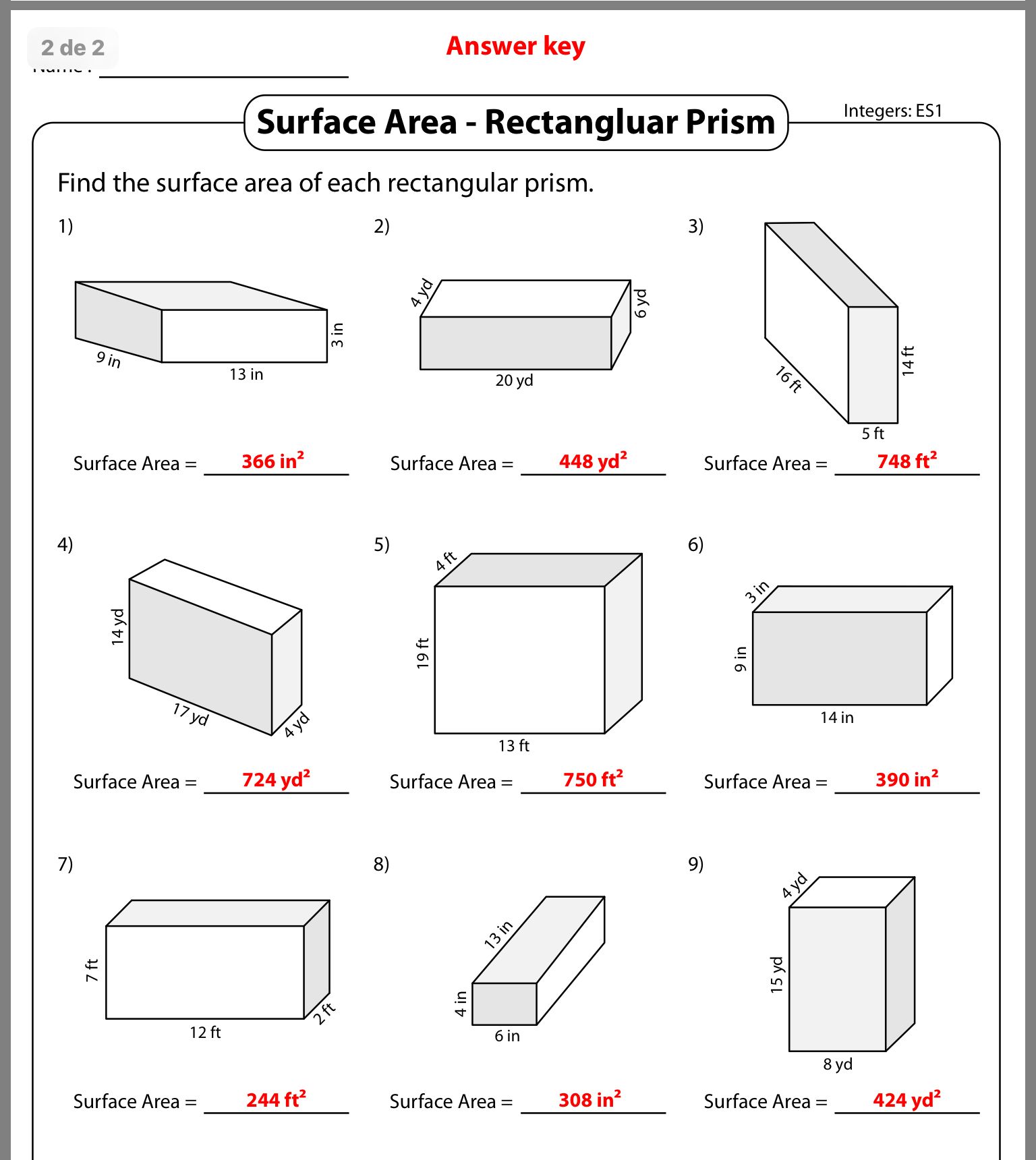
Students can fill in the last column with their calculated surface areas to reinforce learning.
Common Mistakes to Avoid
- Confusing the dimensions: Always ensure you identify the length, width, and height correctly.
- Multiplying dimensions instead of adding areas: Each face's area is calculated separately, then added together.
- Neglecting to double the area for opposite faces.
- Unit errors: Always keep units consistent and square them properly when finding area.
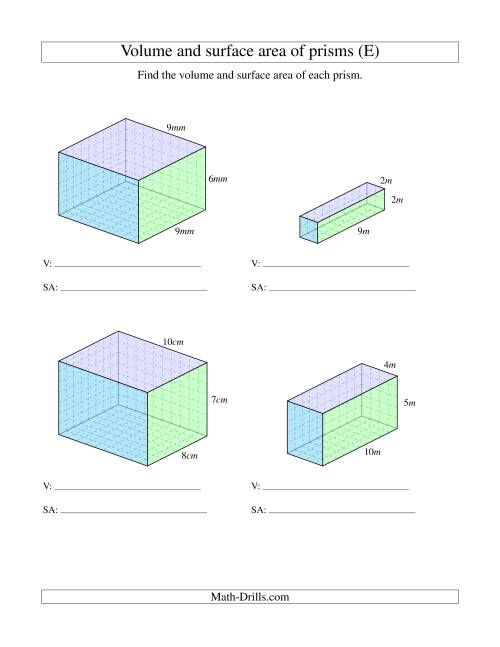
Advanced Challenges

For those looking to stretch their understanding:
- Calculate the surface area when given only the volume and two dimensions.
- Find the dimensions of a rectangular prism given its surface area and one of the dimensions.
- Determine the maximum volume a rectangular prism can have if its surface area is fixed.
These challenges encourage deeper analysis and understanding of the relationship between volume and surface area.
👁️ Note: Remember that as dimensions change, the surface area does not change linearly but changes by the square of the scaling factor.
In summary, mastering the surface area calculations for a rectangular prism not only enhances one's mathematical ability but also provides practical skills applicable in various fields. Through understanding the formula, engaging in practical examples, and practicing with worksheets, learners can gain confidence in geometry. The exploration of surface area opens up numerous possibilities for critical thinking and real-world applications, making it an essential topic in the educational journey of any student.
Why do we double the area of each pair of opposite faces?

+
The surface area formula for a rectangular prism includes doubling the area of each face because there are two faces for each dimension (front and back, left and right, top and bottom).
How does changing one dimension of a rectangular prism affect its surface area?

+
Changing one dimension changes the area of at least two faces, thus altering the total surface area. If you increase or decrease a dimension, the impact on surface area is not linear but exponential.
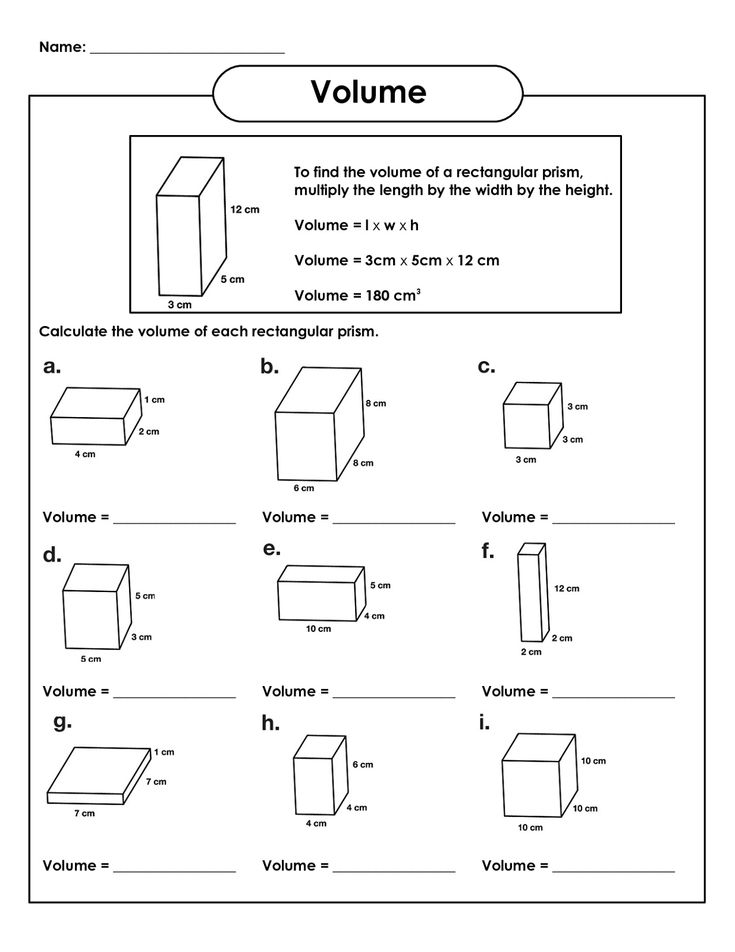
What’s the difference between volume and surface area?

+
Volume measures the three-dimensional space inside a shape, while surface area measures the total area of all the outer surfaces. Volume is calculated in cubic units (like cubic inches), and surface area in square units (like square inches).