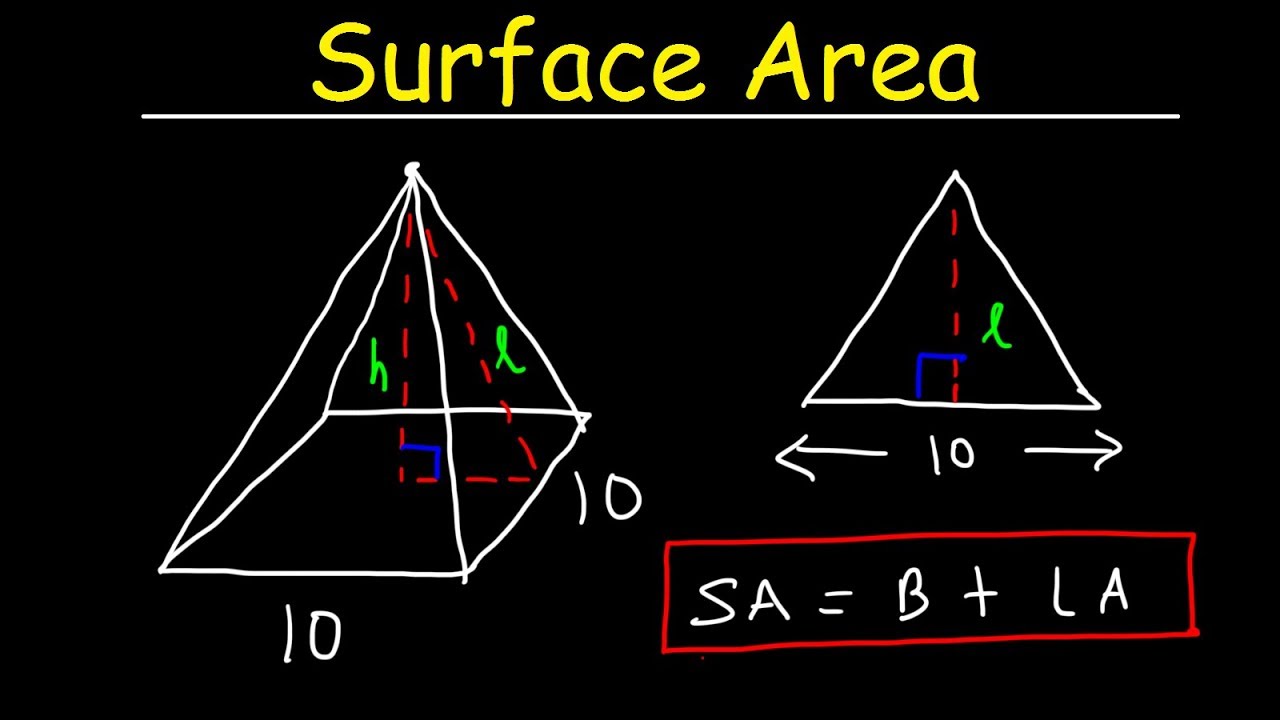
5 Ways to Solve Surface Area of Pyramids

Understanding the Basics of Pyramids

Pyramids have fascinated humans for millennia, not only for their architectural grandeur but also for the mathematical beauty underlying their forms. Before delving into the methods for calculating their surface area, it’s essential to understand some basic terminology:

• Base: The base of a pyramid can be any polygon. For simplicity, we often discuss pyramids with square or triangular bases, but they can theoretically have any shape.
• Vertices: The points where the triangular faces converge at the apex or top of the pyramid.
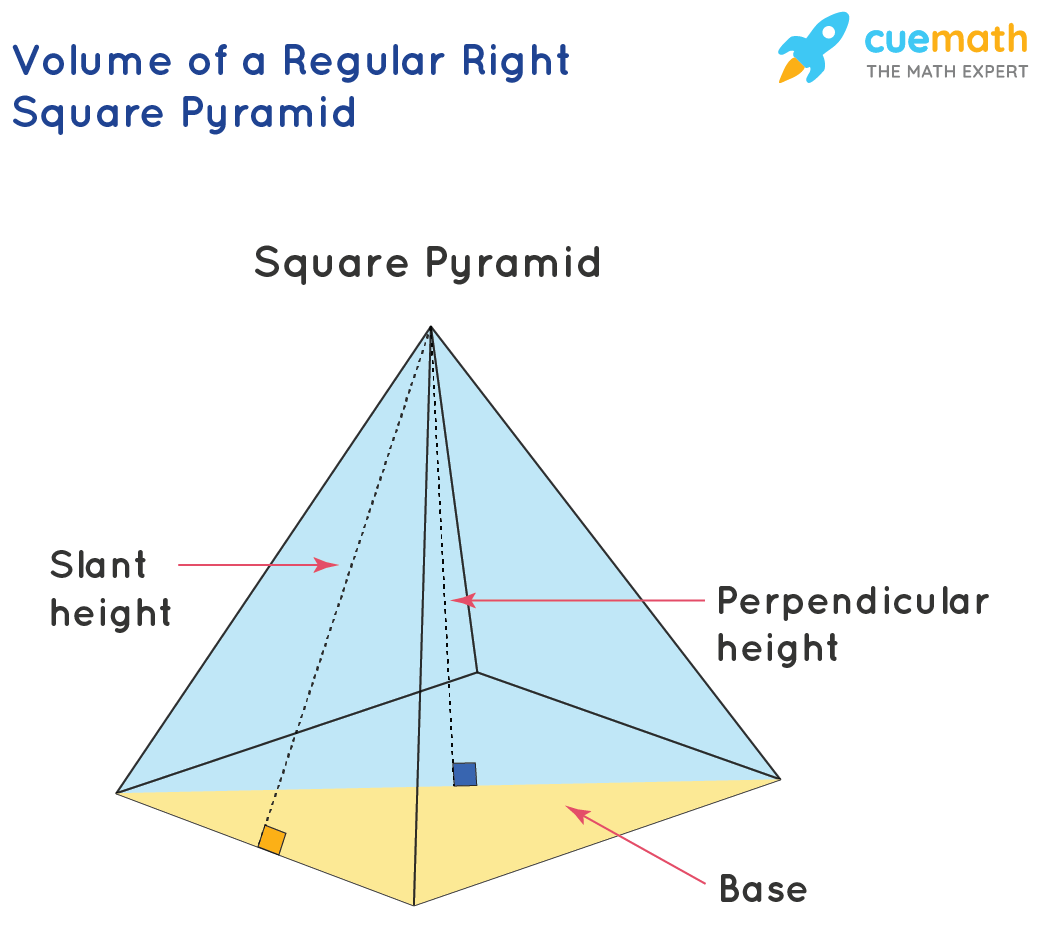
• Height: The perpendicular distance from the apex to the center of the base.
• Slant Height: The height of one of the triangular faces of the pyramid, measured from the midpoint of one of the base edges to the apex.
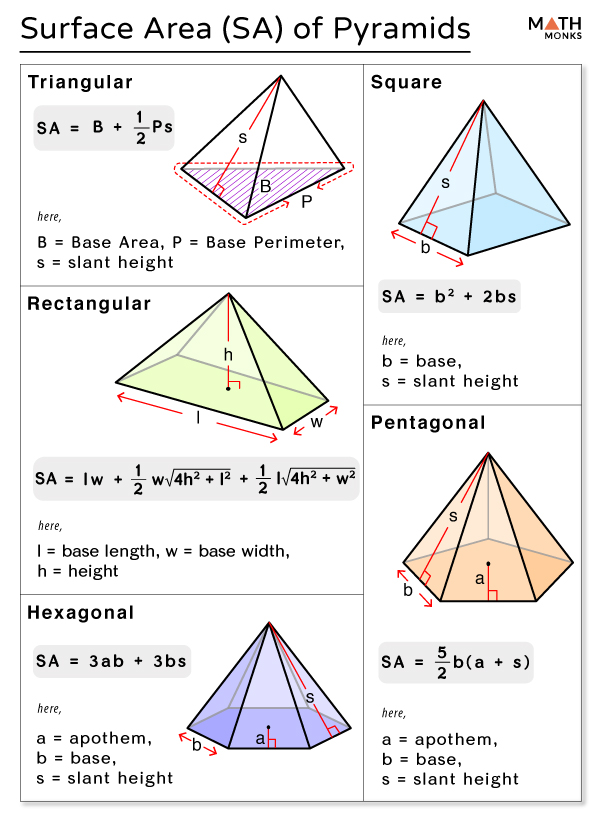
• Area of the Base (A_b): This is calculated depending on the base shape; for a square base, A_b = side²; for a triangular base, A_b = 1/2 * base * height.

Method 1: Using the Slant Height

The simplest way to calculate the surface area of a pyramid involves knowing the slant height:

• Find the area of the base using its specific formula.
• Calculate the area of one triangular face, which can be found using:

Area_triangle = 1/2 * base * slant height

• Since all triangular faces are usually congruent, multiply this area by the number of faces, excluding the base. For a square base pyramid, this would be 4 faces; for a triangular base, it would be 3 faces.
• Add this total to the area of the base.

Method 2: Using Only the Height and Base

If you only know the height of the pyramid and the dimensions of its base:

• Calculate the area of the base.
• Determine the slant height using the Pythagorean theorem with the pyramid's height and half the base's width for a square base pyramid:

slant height = √(height² + (base/2)²)

• Use the slant height to find the area of one triangular face and proceed as in Method 1.

Method 3: Using Coordinate Geometry

This method is particularly useful for irregular pyramids or when you’re given coordinates:

• Place the pyramid in a 3D coordinate system with vertices at specific coordinates.
• Use the distance formula between points to find lengths of edges.
• Apply the formula for the area of any triangle (like Heron's formula or trigonometric approach) to calculate the area of each face.
• Sum all areas to get the total surface area.

Method 4: Using Calculus

Calculus provides a more sophisticated approach, especially for complex pyramids:

• Imagine the pyramid as a stack of infinitesimally thin slices with varying cross-sectional areas.
• Set up an integral where you integrate the area of each slice from the base to the apex.
• This method is particularly useful if the shape of the pyramid's cross-section changes as you move from base to apex.

Method 5: Visualization and 3D Software

Modern technology provides tools for visual learning and precise calculation:

• Utilize 3D modeling software like AutoCAD, Blender, or even educational tools like Geogebra or GeoGebra 3D.
• Create a model of your pyramid, then:
• Use the software to calculate the surface area directly through its tools.
• Or, dissect the model visually, calculating each part’s area and summing them up.

📝 Note: While software is incredibly useful for complex shapes or visual learning, understanding the mathematical approach is crucial for problem-solving in various contexts.

In wrapping up our exploration of how to solve for the surface area of pyramids, each method provides unique insights and advantages. From the straightforward calculations using slant height to the more abstract approaches with calculus or coordinate geometry, you now have a multifaceted toolkit for tackling pyramid-related math problems.

Remember that mathematical elegance often lies in choosing the simplest method for your given situation. Whether you’re calculating for academic purposes, architectural design, or simply out of curiosity, the beauty of pyramids remains in their geometric purity and the harmony of numbers that define their existence.

What is the most efficient method to calculate the surface area of a pyramid with a square base?

+

For a pyramid with a square base, using the slant height method (Method 1) is often the most efficient, especially if you’re given the slant height directly. It involves fewer calculations than determining the slant height from the height and base dimensions.

Can calculus be used to find the volume of a pyramid?

+

Yes, calculus can find the volume of a pyramid through integration. By treating the pyramid as a stack of infinitely thin slices, you can integrate the cross-sectional area as you move from the base to the apex.

How do you calculate the surface area of a pyramid if the base is not a regular polygon?

+

If the base is not a regular polygon, you’ll need to break down the problem into steps: Calculate the area of the base using the polygon’s vertices, then compute each triangular face’s area individually, considering their unique properties, and sum all these areas for the total surface area.