5 Tips for Calculating Pyramid and Cone Surface Area
If you're diving into the world of geometry, understanding how to calculate the surface area of three-dimensional shapes like pyramids and cones is crucial. These geometric figures are not only fascinating but also frequently encountered in various fields such as architecture, engineering, and even in simple everyday objects. Here, we'll explore five insightful tips to help you master the calculation of surface area for pyramids and cones with ease.
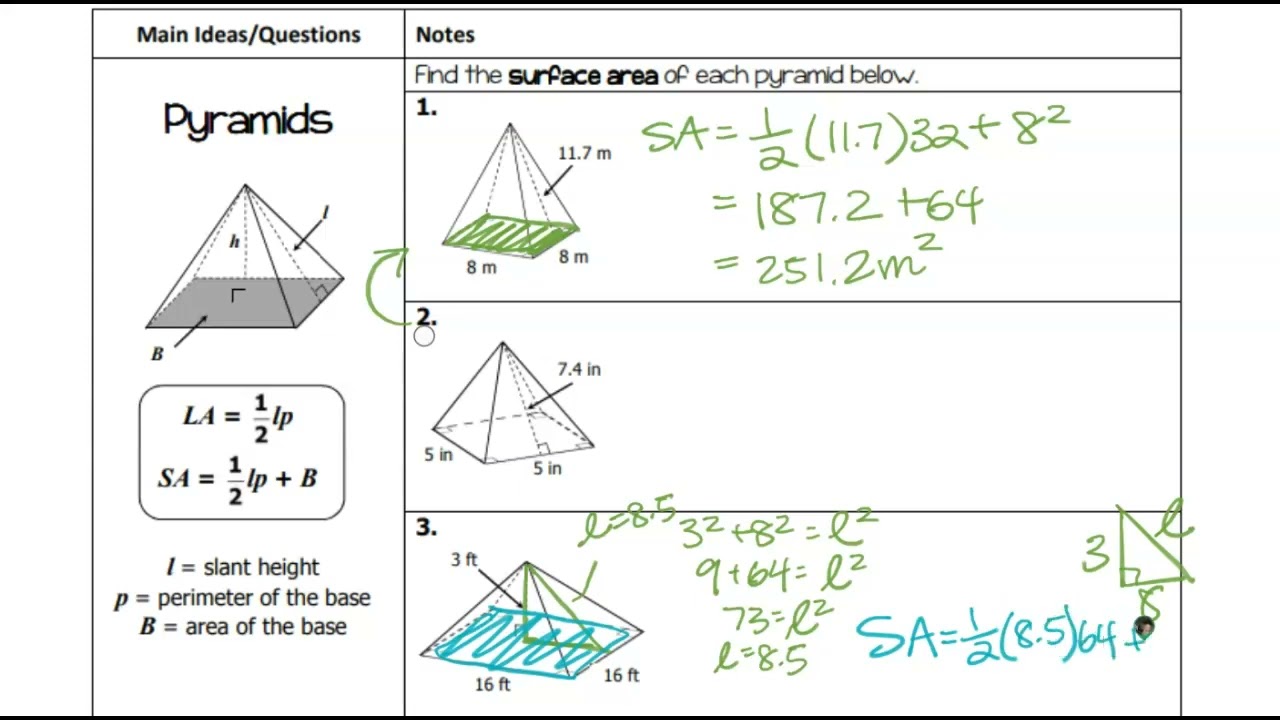
Tip #1: Understand the Shape and Its Components
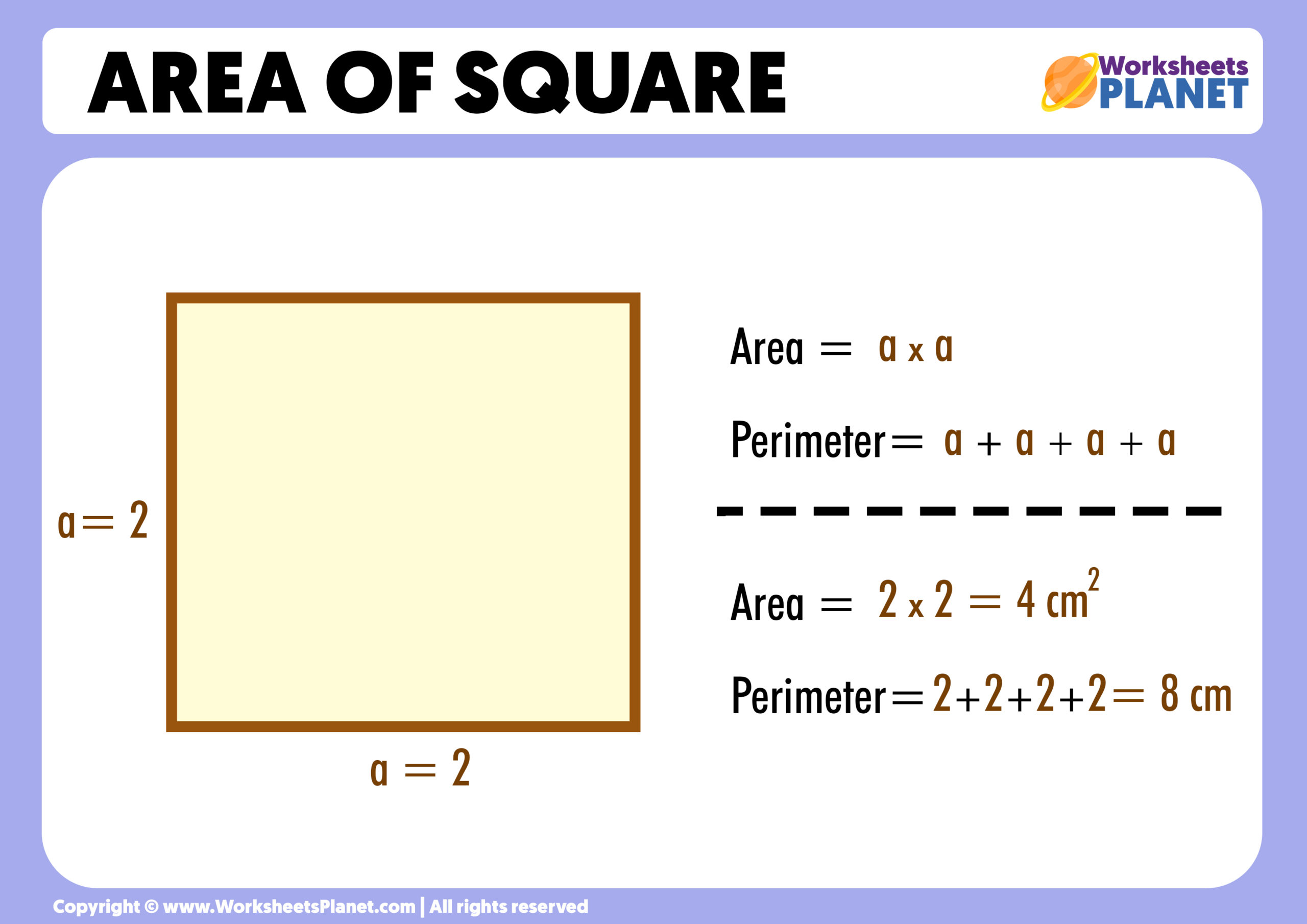
Before diving into calculations, familiarize yourself with the shapes:
- Pyramid: A pyramid has a base, which could be any polygon, and triangular faces meeting at a common vertex. Key elements include the base perimeter, slant height, and base area.
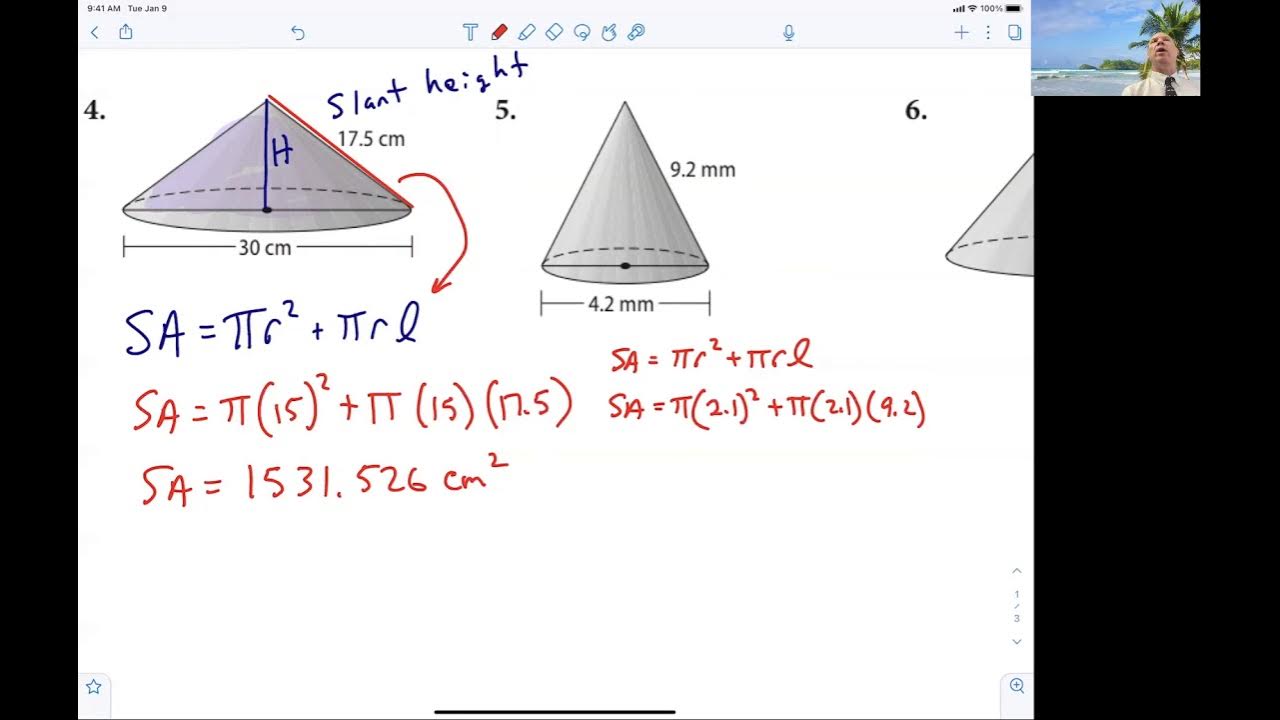
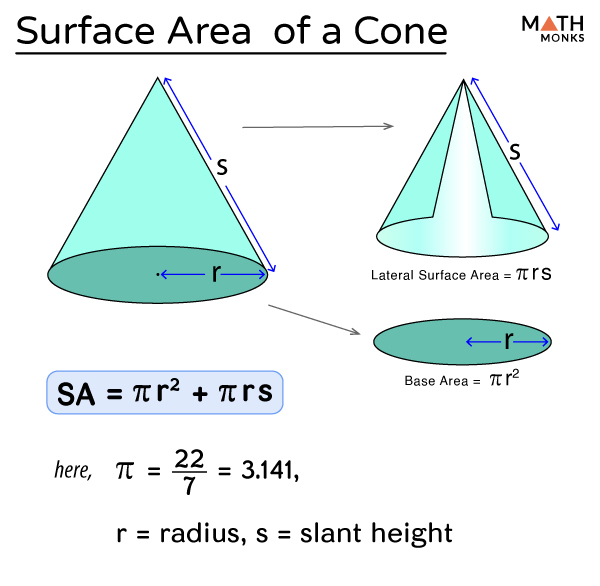
- Cone: Cones have a circular base with a curved surface tapering to a single point or vertex. The essential components are the base radius, slant height, and height.
📐 Note: The base shapes can vary; for example, regular pyramids use regular polygons as their bases, and cones are mostly circular.
Tip #2: Master the Formulas
To calculate surface areas, you need to know the correct formulas:
For Pyramids:

- Base Area (B) = Area of the base polygon.
- Surface Area (SA) = B + (number of faces × area of one triangular face).
where the area of one triangular face = ½ × base × slant height (l).
For Cones:

- Base Area (B) = πr2.
- Curved Surface Area (CSA) = πrl.
- Surface Area (SA) = πr2 + πrl.
💡 Note: Remember that r stands for radius, and l for slant height in these formulas.
Tip #3: Apply Trigonometry

Often, you might not have the slant height given directly. Here’s how to find it:
- For pyramids, use the Pythagorean theorem where the slant height (l) is the hypotenuse of a right triangle formed by the height of the pyramid and the height of one triangular face.
- For cones, again use the Pythagorean theorem with the cone’s height, base radius, and slant height.
Tip #4: Use Visual Aids and Models

Visual aids are immensely helpful:
- Make or find a model of the pyramid or cone. Dissecting the model can provide a clearer understanding of its surface.
- Draw the net of the shape (unfolded flat version) to visualize how each part contributes to the total surface area.
| Shape | Net Representation |
|---|---|
| Pyramid | Base + Triangular Faces |
| Cone | Circle + Sector |
📊 Note: Visualizing the shapes helps in remembering their formulas and components.
Tip #5: Practice with Real-World Examples

To truly understand these calculations, apply them to real-life scenarios:
- Estimate the material needed to cover a conical roof or a pyramid tent.
- Compare the surface areas of different sized ice cream cones or party hats.
By applying these tips, you'll not only improve your understanding but also your speed and accuracy in calculating surface areas of pyramids and cones. Geometry becomes much less abstract when you connect it to real-world applications, making these calculations not just a theoretical exercise but a practical skill.
Why is the slant height important?

+
The slant height is crucial because it helps determine the area of the triangular or curved surfaces in pyramids and cones, respectively, which is essential for calculating total surface area.
Can these formulas be applied to any pyramid or cone?

+
Yes, but you must adjust for the shape of the base or the nature of the cone (like if it’s frustum). For irregular bases, you would need to calculate each triangular face’s area individually.
How can I ensure my calculations are accurate?

+
Use accurate measurements, double-check your math, and apply practical real-world scenarios as a sanity check for your results.
What’s the difference between volume and surface area?

+
Volume measures the space inside a shape, while surface area measures the total area covering the shape’s surface.
Can these calculations help in other areas of study?

+
Absolutely! They are relevant in fields like architecture, engineering, and even in arts and crafts for calculating materials needed or space occupied.