Master Surface Area: Prisms and Pyramids Worksheet Guide

Understanding the intricacies of geometry, particularly how to calculate surface areas, can be a challenging but rewarding endeavor. This comprehensive guide is dedicated to helping both students and educators master the concepts of surface area for prisms and pyramids through a detailed worksheet approach. Whether you're preparing for an exam or looking to deepen your understanding of geometric shapes, this guide will serve as your roadmap.
The Fundamentals of Surface Area

The surface area of a three-dimensional object is the total area that the surface of the object occupies. For prisms and pyramids, this involves summing up the areas of all their faces, which can vary significantly based on their shapes.
- Rectangular Prism: Sum of the areas of six rectangles.
- Triangular Prism: Sum of two triangular bases and three rectangular sides.
- Pentagonal Prism: Sum of five rectangular sides and two pentagonal bases.
- Square Pyramid: Base plus four triangular faces.
- Triangular Pyramid: All four triangular faces.
Calculating the Surface Area of Prisms
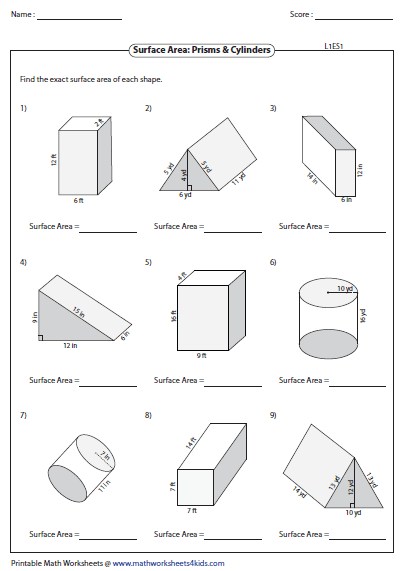
Prisms have two identical, parallel bases and a set of rectangular lateral faces. Here's how to approach calculating their surface areas:
| Shape | Area Formula |
|---|---|
| Rectangular Prism | 2(lw + lh + wh) |
| Triangular Prism | bh + Perimeter × Height |
| Pentagonal Prism | 5sh + 5/2 × s² × sin(72°) |

📌 Note: In the formulas above, l, w, h, b, s, and h refer to the length, width, height, base, side length, and height of the respective prisms.
Calculating the Surface Area of Pyramids
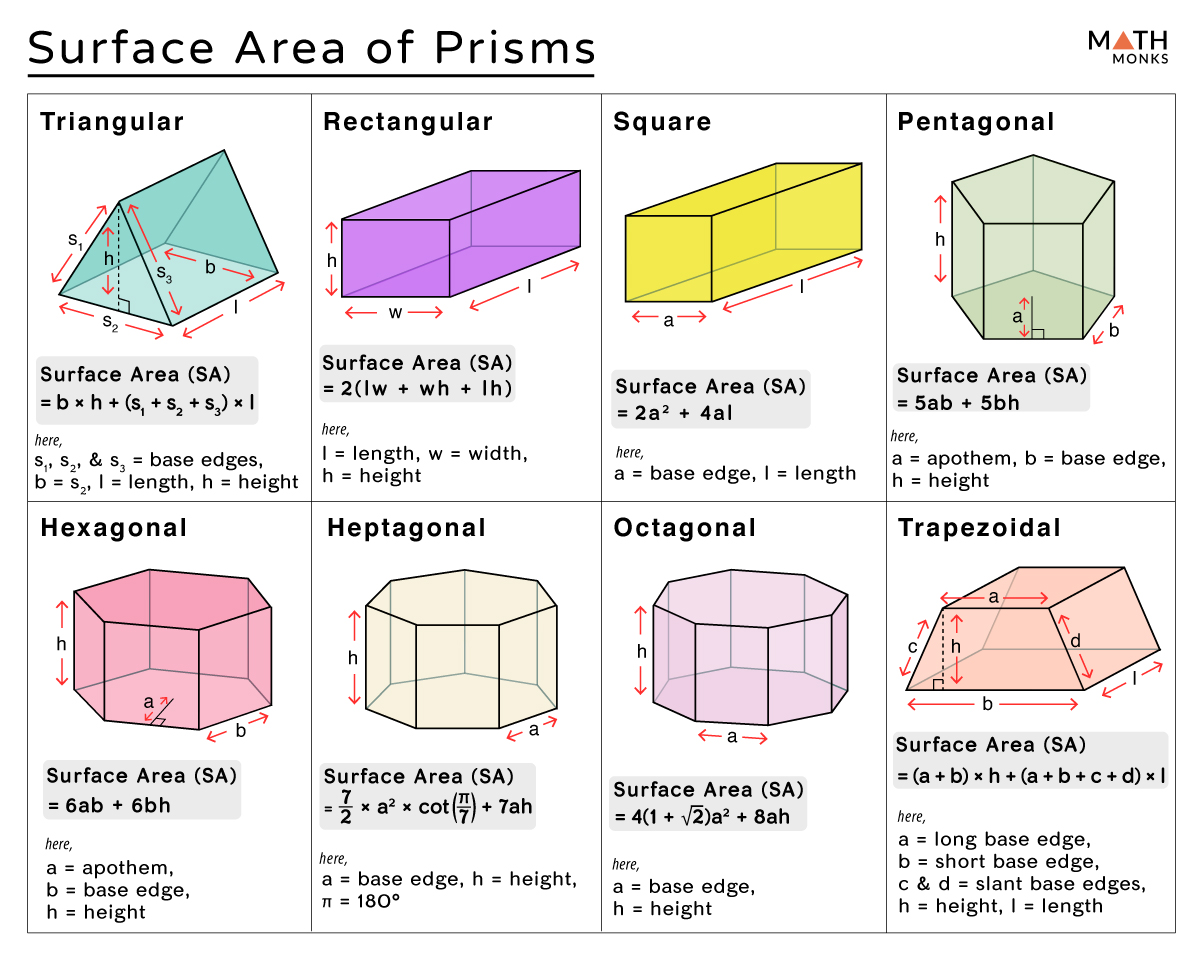
Pyramids have a single base and triangular faces that meet at a common vertex. The formula to calculate their surface areas involves:
- Base Area: Depends on the shape of the base (e.g., square, triangle).
- Lateral Face Area: Area of the slant height times the perimeter of the base, divided by 2 for triangular sides.
Worksheet Design for Surface Area

To effectively learn these concepts, structuring a worksheet is crucial:
- Introduction: A brief overview of what surface area represents.
- Theory Recap: Key formulas and concepts to remember.
- Examples: Work through examples step-by-step.
- Practice Problems: Vary from simple to complex, covering different shapes.
- Challenge Questions: Test advanced understanding with word problems or real-life applications.
🔖 Note: Always include hints or references to formulas, as this helps in both independent and guided practice.
Examples and Practice Problems

Here are some examples and practice problems to get started:
Rectangular Prism Example
Given a rectangular prism with dimensions of 3 cm, 4 cm, and 5 cm, calculate its surface area:
- Surface Area = 2(3*4 + 3*5 + 4*5) = 94 cm²
📝 Note: Students should be encouraged to label their work clearly to avoid confusion.
Triangular Pyramid Example
Consider a triangular pyramid with a base side of 6 cm and a slant height of 5 cm:
- Surface Area = 6 × 6 / 2 + 3 × 6 × 5 / 2 = 48 cm²
Common Pitfalls and How to Avoid Them

Geometry, like any subject, comes with its challenges:
- Misinterpretation of Dimensions: Always check which dimension is which before calculating.
- Forgotten Faces: Keep a count of all the faces of the shape.
- Slant Height vs. Vertical Height: Use the right height in the right context.
The Benefits of Mastering Surface Area

Understanding surface area extends beyond academic geometry. Here are some real-world applications:
- Design and Architecture: Calculating surface areas is crucial in designing buildings and understanding material needs.
- Manufacturing: Efficient production requires exact measurements for material use.
- Science Experiments: Volume and surface area ratios are pivotal in experiments like diffusion and osmosis.
To sum up, mastering the surface area of prisms and pyramids not only empowers students to excel in geometry but also equips them with skills valuable in many career paths. By approaching this topic methodically through practice, understanding the principles, and applying real-world examples, students can transcend mere memorization to gain a profound understanding of spatial relationships and volume. The journey through geometry is not just about numbers and shapes; it's about developing critical thinking, problem-solving, and spatial visualization skills that are essential in both academic and real-life contexts.
What is the difference between volume and surface area?

+
Volume measures the amount of space inside a three-dimensional object, while surface area measures the total area of the outer surfaces of the object.
How do you calculate the surface area of an irregular shape?

+
For irregular shapes, you can approximate the surface area by breaking the shape down into simpler, regular shapes, calculating their areas, and then summing them up. This method can be applied to complex shapes using techniques like Riemann sums.
Why is understanding surface area important?
+
Understanding surface area helps in fields like architecture, where knowing how much material is needed to cover a building is crucial; in manufacturing, to optimize material use; and in science, to understand phenomena like heat transfer, chemical reactions, and even biological processes.