Surface Area of Prisms and Pyramids: Practice Worksheet

Understanding how to calculate the surface area of prisms and pyramids is a fundamental skill in geometry. This practice worksheet will guide you through various problems to hone your proficiency in this area. Whether you're a student aiming to excel in math or someone curious about the intricacies of geometric shapes, this post will serve as a comprehensive resource.
Understanding Prisms and Pyramids
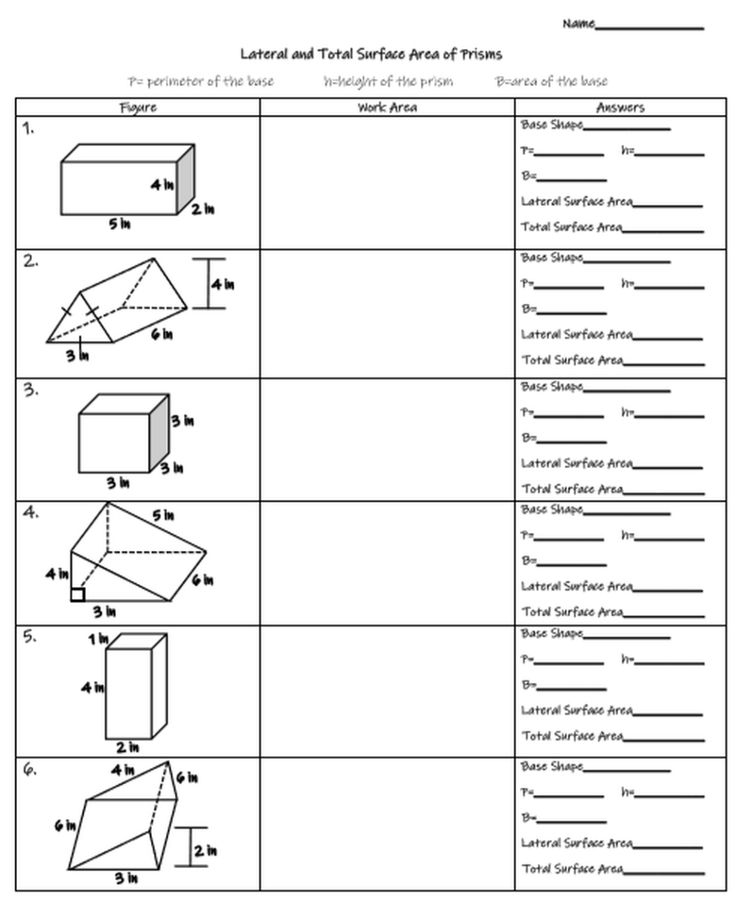
Let's start with some basic definitions:
- Prisms are three-dimensional shapes with a uniform cross-section, having identical parallel bases joined by rectangular sides.
- Pyramids have one base that is a polygon and triangular faces meeting at a common vertex known as the apex.
Formula for Surface Area of Prisms
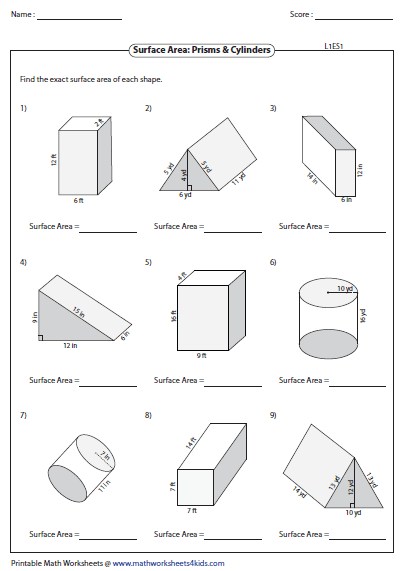
To find the surface area of a prism:
- Calculate the area of both bases.
- Sum the areas of all the rectangular lateral faces.
- Add the areas of the bases and lateral faces.
The general formula is:
Surface Area (SA) = 2 × Area of Base + Perimeter of Base × Height of Prism
Formula for Surface Area of Pyramids

The steps to find the surface area of a pyramid are slightly different:
- Calculate the area of the base.
- Find the area of each triangular side.
- Sum these areas together.
The formula can vary based on the shape of the base but for a pyramid with a polygon base, it's:
Surface Area (SA) = Area of Base + (½ × Perimeter of Base × Slant Height)
Practical Examples

Example 1: Rectangular Prism


- Base area = length × width = 5 cm × 4 cm = 20 cm²
- Perimeter of the base = 2(length + width) = 2(5 + 4) = 18 cm
- Height of the prism = 6 cm
- Surface Area = 2 × 20 cm² + 18 cm × 6 cm = 100 cm²
Example 2: Triangular Pyramid (Tetrahedron)


- Base area = ½ × base × height of triangle = ½ × 8 cm × 7 cm = 28 cm²
- Perimeter of the base = 3 × 8 cm = 24 cm
- Slant height = 7 cm
- Surface Area = 28 cm² + (½ × 24 cm × 7 cm) = 112 cm²
📝 Note: These examples use simple shapes to illustrate the calculation process. In real-world applications, the shapes might be irregular or more complex.
Key Points for Calculating Surface Area

- Always ensure you are calculating the correct areas - base and lateral.
- For irregular bases, use the formula specific to the shape of the base.
- Slant height is used for pyramids, not the height perpendicular to the base.
Throughout your practice, you'll find that these calculations become intuitive. Here are some additional tips:
Tips for Efficiency

- Use consistent units of measurement.
- Break down complex shapes into simpler ones if possible.
- Visual aids like diagrams can help in understanding the problem better.
In summary, mastering the calculation of surface areas for prisms and pyramids involves understanding the shapes, recognizing the correct formulas, and applying them with precision. This practice will not only enhance your geometric understanding but also prepare you for more complex mathematical challenges. Keep practicing, and over time, these calculations will become second nature.
How can I differentiate between a prism and a pyramid?

+
A prism has two identical parallel bases, while a pyramid has a single base with triangular faces meeting at an apex.
Why is slant height important in calculating pyramid surface area?

+
Slant height is used in the formula for the lateral faces, which are triangles, to find their areas correctly.
What happens if the base of a prism or pyramid isn’t a regular shape?

+
You would have to use the formula for the specific polygon shape of the base and calculate the area of each face individually before summing them up.



