Mastering Cylinder Surface Area: Worksheet Guide
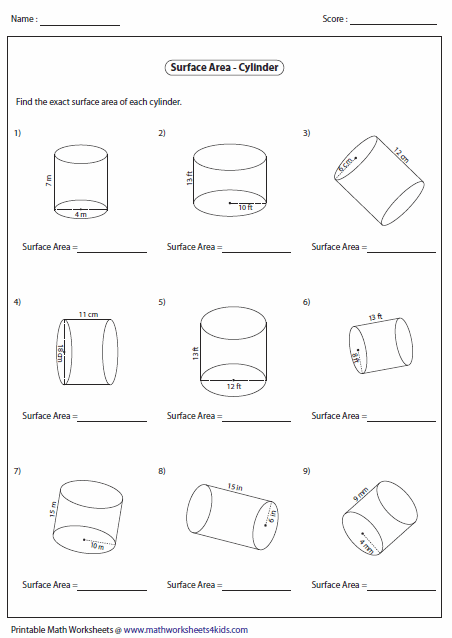
In this comprehensive guide, we delve into the fascinating world of cylinder surface area calculations. This isn't just about academic learning; understanding how to calculate the surface area of a cylinder has practical applications in fields like engineering, architecture, and even in everyday life when you might be tasked with figuring out paint needs or material estimates for cylindrical structures. This worksheet guide aims to be your companion in mastering these skills.
Understanding the Geometry of a Cylinder

Before we delve into the mathematics of surface area, let’s revisit the geometry of a cylinder:
- Cylinder: A three-dimensional shape with two parallel bases, typically circles.
- Radius: The distance from the center to the edge of the circular base.
- Height: The perpendicular distance between the two circular bases.
🔍 Note: For simplicity, we often assume the cylinder to be a “right circular cylinder” where the axis is perpendicular to the base, though the principles can extend to more complex forms.
Formula for Cylinder Surface Area

The total surface area of a cylinder includes:
- The area of the top and bottom bases:
- The area of the curved surface:
The formula can be expressed as:
| Top + Bottom: | 2πr2 |
| Curved Surface: | 2πrh |

Thus, the total surface area formula becomes:
Total Surface Area = 2πr2 + 2πrh
Step-by-Step Calculation Guide
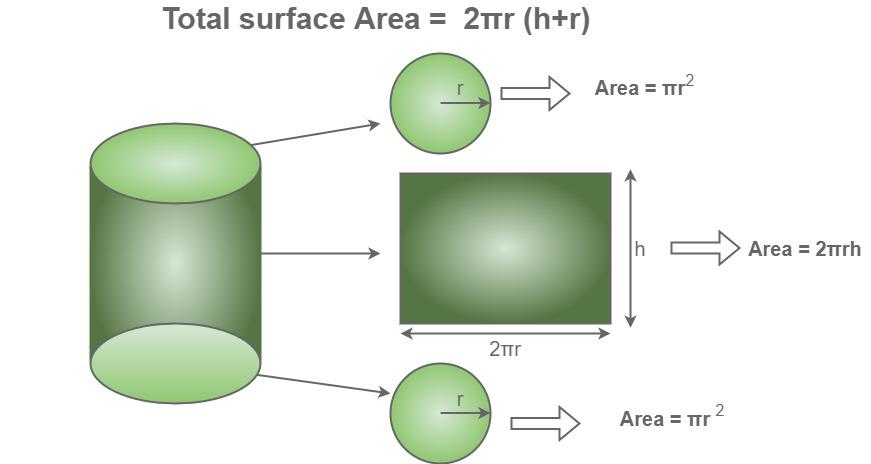
Let’s break down how to calculate the surface area of a cylinder:
1. Identify the Measurements
- Radius: Measure the radius of the base.
- Height: Measure the height or the distance between the bases.
2. Apply the Formula

- Calculate the area of the two bases: 2πr2
- Calculate the area of the curved surface: 2πrh
- Add these together to get the total surface area.
3. Solving a Sample Problem
Suppose we have a cylinder with a radius of 5 cm and a height of 12 cm:
- Area of the bases: 2 * π * 52 = 157.08 cm2
- Curved surface area: 2 * π * 5 * 12 = 376.8 cm2
- Total Surface Area: 157.08 + 376.8 = 533.88 cm2
📘 Note: Always use appropriate units; if your inputs are in centimeters, your answer will also be in square centimeters.
Practical Applications

Understanding cylinder surface area has various applications:
- Paint Calculations: How much paint do you need to cover a cylindrical container?
- Material Estimates: Estimating fabric or metal needed for cylindrical structures.
- Volume Determinations: In engineering, knowing the surface area can help in calculating material stresses or design parameters.
Common Pitfalls and Tips

- Remember to use the radius and not the diameter in the formula.
- Ensure consistency in units of measurement.
- If you’re dealing with an open-top cylinder, remember to exclude the top base from your calculations.
💡 Note: Be cautious when dealing with real-world measurements; often, you’ll need to account for seams, wastage, or other practical considerations.
Throughout this guide, we've explored how to calculate the surface area of a cylinder from basic geometry to practical application. With this knowledge, you're now equipped to tackle cylinder-related problems in both academic and real-life contexts. This isn't just about numbers but about understanding the world through its dimensions.
Why do we need to know the surface area of a cylinder?

+
Knowing the surface area is useful for determining how much material is needed to cover or construct cylindrical objects, like in construction, packaging, or even paint estimations.
Can the formula for surface area change if the cylinder has an open top?

+
Yes, if the cylinder has an open top, you’ll exclude the area of the top base from the formula. Thus, the formula would be πr2 + 2πrh.
How accurate should my measurements be when calculating surface area?

+
For most practical applications, accurate to the nearest centimeter or inch is often sufficient. However, in precision-based fields like manufacturing or engineering, measurements might need to be more precise.