5 Quick Worksheets to Master Cube Surface Areas

Mastering the calculation of the surface area of a cube is fundamental for students exploring the world of geometry. It's an essential skill that not only helps in understanding 3D shapes but also in solving real-world problems like estimating packaging materials or architectural designs. This guide provides five comprehensive worksheets designed to ensure you gain a thorough understanding of cube surface area calculation. Each worksheet builds upon the previous one, offering varied problem types to solidify your grasp on this geometrical concept.
Worksheet 1: Basics of Cube Surface Area

Here, we start with the fundamentals. This worksheet is for beginners or those looking to refresh their memory:
- Calculate the surface area of cubes given edge lengths.
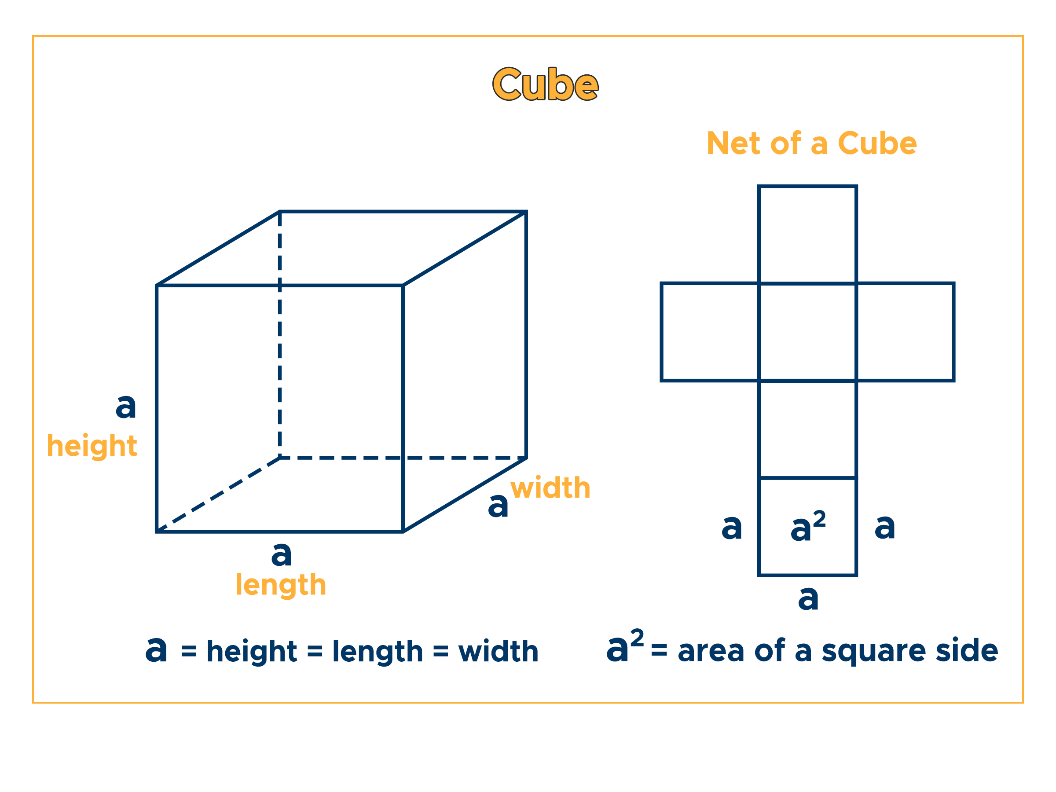
- Understand that a cube has 6 faces, all identical.
- Formula reminder: Surface Area = 6a2
📏 Note: Remember, all edges of a cube are equal, making calculations straightforward.

Worksheet 2: Real-world Application Problems
Now that you’ve got the basics down, let’s dive into how this knowledge applies to real-life scenarios:
- Calculate the amount of paint needed to paint a cubic box.
- Determine the wrapping paper needed for a cubic gift.
- Find the surface area for insulation on a small cube-shaped ice chest.
These problems not only test your calculation skills but also enhance your problem-solving abilities.
Worksheet 3: Comparing Surface Areas

This worksheet focuses on comparing the surface areas of different cubes, providing deeper insights:
- Compare cubes with different edge lengths.
- Determine which cube has a larger or smaller surface area.
- Identify how changes in edge length affect surface area.
🌐 Note: Surface area grows proportionally to the square of the edge length, not linearly.

Worksheet 4: Deriving Surface Area Formulas
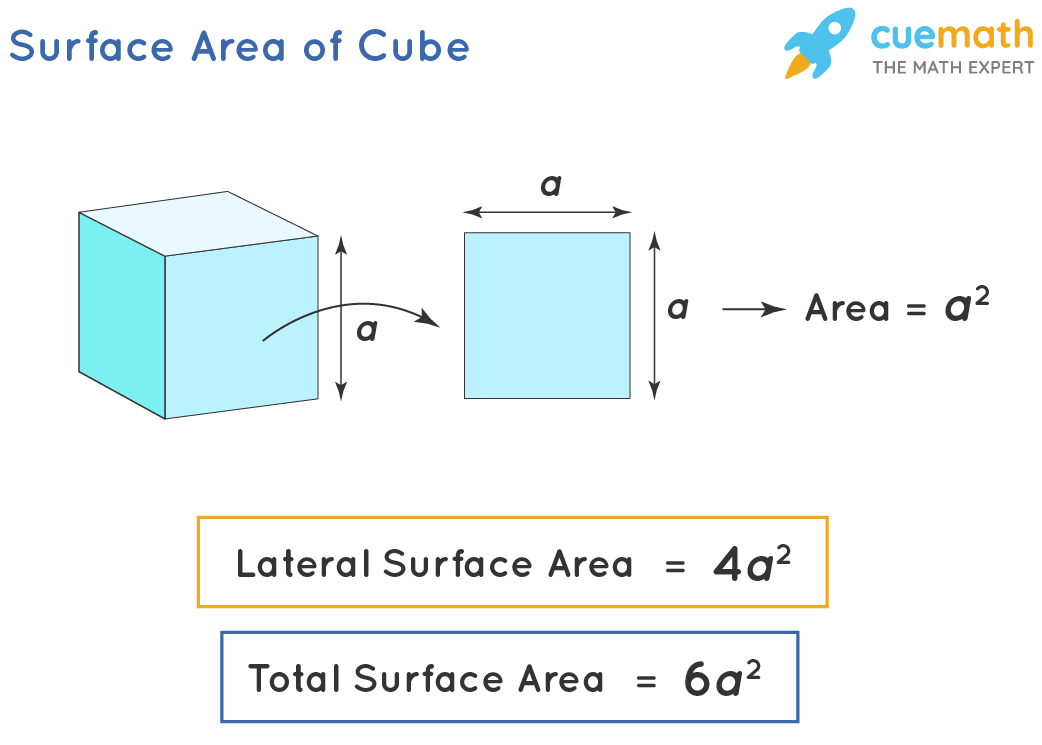
Here, you’ll delve into the derivation of the surface area formula, promoting a deeper understanding:
- Derive the formula from a basic cube.
- Extend this derivation to understand how surface area relates to volume.
This exercise is particularly useful for students who want to see the “why” behind the formula.
Worksheet 5: Word Problems and Complex Calculations

The final worksheet is for those ready for a challenge:
- Solve problems where dimensions are given in different units.
- Analyze scenarios where the surface area influences the cube’s function or appearance.
- Incorporate partial measurements and approximation into calculations.
This worksheet is designed to push your understanding beyond straightforward calculations, fostering a well-rounded geometrical knowledge.
🔍 Note: Remember to convert units when necessary, and always double-check your results!
By working through these five worksheets, you will have not only mastered the calculation of a cube's surface area but also gained insights into how this knowledge applies to various practical scenarios. From understanding the basics to deriving formulas and tackling complex problems, these exercises ensure you are proficient in one of geometry's key concepts. As you progress, remember to reflect on how changes in a cube's dimensions affect its surface area and volume, connecting these ideas to broader mathematical principles.
Why is it important to learn how to calculate a cube’s surface area?

+
Understanding surface area is vital for various fields like architecture, packaging, and engineering, where materials and costs depend on the amount of surface to cover or treat.
Can I use these worksheets if I’m not a student?

+
Absolutely. These worksheets are helpful for anyone looking to enhance their understanding of geometry or needing to apply these principles in practical situations.
How can I extend my learning beyond these worksheets?

+
Consider exploring 3D modeling software or delve into other shapes like spheres, cylinders, and cones to broaden your geometric knowledge.



