5 Ways to Master Cone Surface Area Calculations
Understanding how to calculate the surface area of a cone is a crucial skill in geometry, applicable in a variety of real-world scenarios from crafting paper cones to engineering. This blog post will guide you through five effective ways to master cone surface area calculations, ensuring you can tackle any problem with confidence.
1. Learn the Basic Formula

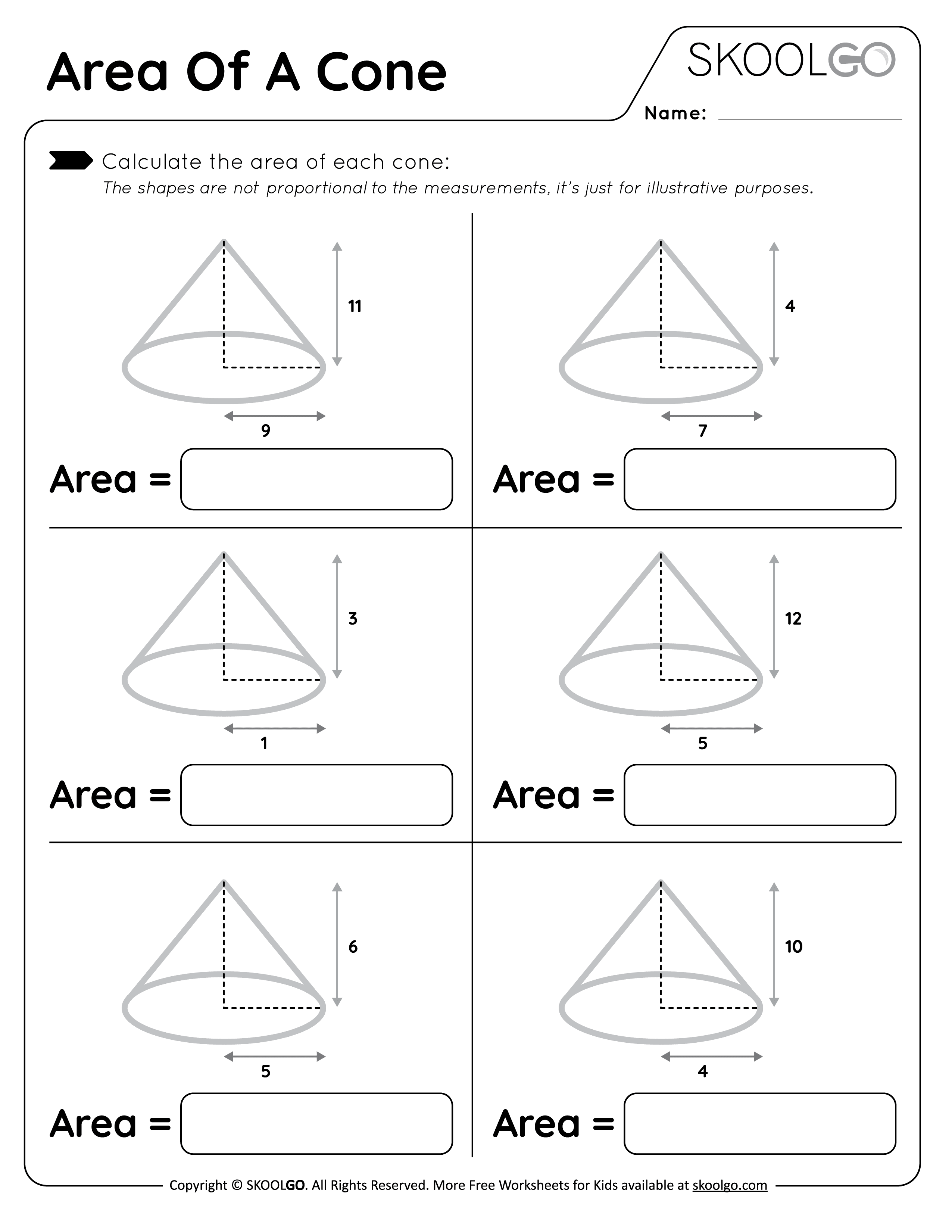
The most fundamental method involves using the formula for the surface area of a cone:
- Lateral Surface Area (LSA): πrL (where r is the radius of the base and L is the slant height).
- Total Surface Area (TSA): πrL + πr2 (where πr2 is the area of the base).
To master this formula:
- Memorize the equations for both the lateral and total surface area.
- Practice calculating r, L, and other related measurements.
Here’s an example:
| Radius ® | Slant Height (L) | π | Lateral Surface Area | Total Surface Area |
|---|---|---|---|---|
| 3 cm | 5 cm | 3.1416 | 3.1416 * 3 * 5 = 47.12 cm2 | 47.12 + (3.1416 * 32) = 75.39 cm2 |

🎓 Note: The slant height can be found using Pythagoras' theorem if you know the radius and the height (h) of the cone: L = √(r2 + h2).
2. Utilize Online Calculators
Online calculators can be a quick way to verify your calculations, especially for complex cones or when working on the go:
- Enter the known dimensions into a reliable online cone surface area calculator.
- Check if the calculator provides both lateral and total surface area calculations.
However, reliance on these tools should not replace understanding the math behind the calculation.
3. Derive the Formula

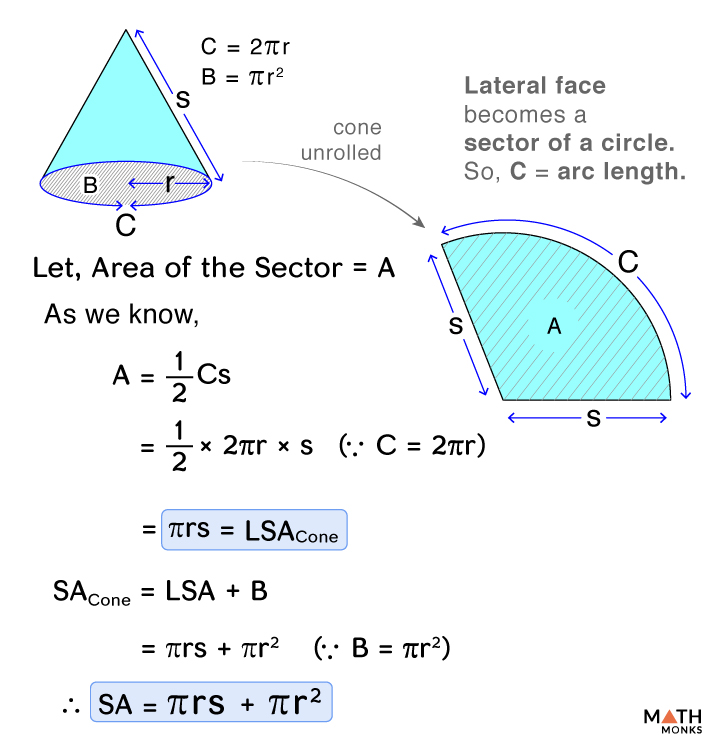
Understanding the derivation of the formula can give you a deeper insight into why it works:
- The cone can be ‘unwrapped’ into a sector of a circle. The sector’s arc length is equal to the circumference of the cone’s base (2πr).
- The slant height becomes the radius of this sector.
- The area of this sector is what gives us the formula for the lateral surface area.
Deriving this process not only solidifies your knowledge but also helps in understanding how cone surface area relates to other geometric shapes.
4. Practical Applications

Apply cone surface area calculations to real-life scenarios to enhance your learning:
- Create physical models: Craft paper cones and measure their dimensions to verify calculations.
- Calculate material needed: When planning to construct a cone-shaped roof or a funnel, determine the amount of material required.
- Estimate volume and weight: Understanding surface area helps in calculating volume, which can lead to weight estimations for packaging.
By integrating the theoretical with the practical, you make your learning more tangible and memorable.
5. Visualize and Simulate

Visualization tools and simulations can offer a visual understanding:
- Use 3D geometry software to manipulate and visualize cones in various dimensions.
- Simulate different cone shapes to see how changes in dimensions affect surface area.
- Take advantage of interactive apps or websites that allow you to change variables and see the results in real-time.
Visualization can help bridge the gap between theory and practice, making abstract calculations easier to grasp.
In summary, mastering cone surface area calculations involves a blend of memorization, practice, understanding, and application. By combining traditional methods with modern tools and practical exercises, you not only gain proficiency but also develop a deeper appreciation for geometry's real-world applications. Whether you're preparing for exams, working on DIY projects, or engaged in professional design, these techniques will serve you well.
How do I find the radius if I know the surface area of a cone?

+
If you know the total surface area (TSA) and the slant height, you can solve for the radius using the formula TSA = πr2 + πrL. Rearrange the equation to isolate r.
What’s the difference between lateral and total surface area?
+
The lateral surface area includes only the curved surface of the cone, while the total surface area includes the base as well.
Can I calculate cone surface area if I only know the height and radius?

+
Yes, you can find the slant height first using Pythagoras’ theorem (L = √(r2 + h2)) and then apply the surface area formulas.