Prisms and Cylinders: Mastering Surface Area and Volume

Understanding the principles behind calculating surface area and volume is crucial, especially when dealing with shapes like prisms and cylinders. These geometric forms are not only a staple in mathematics but also find practical applications in various fields such as architecture, engineering, and product design. In this in-depth exploration, we'll delve into the definitions, formulas, and real-world applications of prisms and cylinders, providing you with a robust understanding of how to calculate their surface area and volume.
The Basics of Prisms and Cylinders


Before diving into the complex calculations, let’s clarify what these shapes are:
- Prisms: A prism is a polyhedron with two parallel, congruent polygonal faces, known as the bases, and rectangular lateral faces.
- Cylinders: A cylinder has a curved lateral face and two congruent circular bases.
Understanding Surface Area

Surface area refers to the total area covering the outer surfaces of an object. Here’s how to calculate it for prisms and cylinders:
Surface Area of Prisms

To find the surface area of a prism:
- Calculate the area of each face.
- Sum the areas of all faces.
⚙️ Note: For prisms with triangular, rectangular, or any other polygonal bases, the lateral area involves summing the areas of the lateral faces.
| Formula | Description |
|---|---|
| Base Area (A) | Area of the base shape (triangle, rectangle, etc.) |
| Lateral Area (L) | Perimeter of the base × Height of the prism |
| Total Surface Area (SA) | A + L + A |

Surface Area of Cylinders

The surface area of a cylinder consists of:
- The areas of the two circular bases: (2πr^2).
- The lateral surface area: (2πrh), where (r) is the radius and (h) is the height.
⚙️ Note: The formula simplifies to (2πr^2 + 2πrh) when adding the top and bottom bases to the lateral surface area.
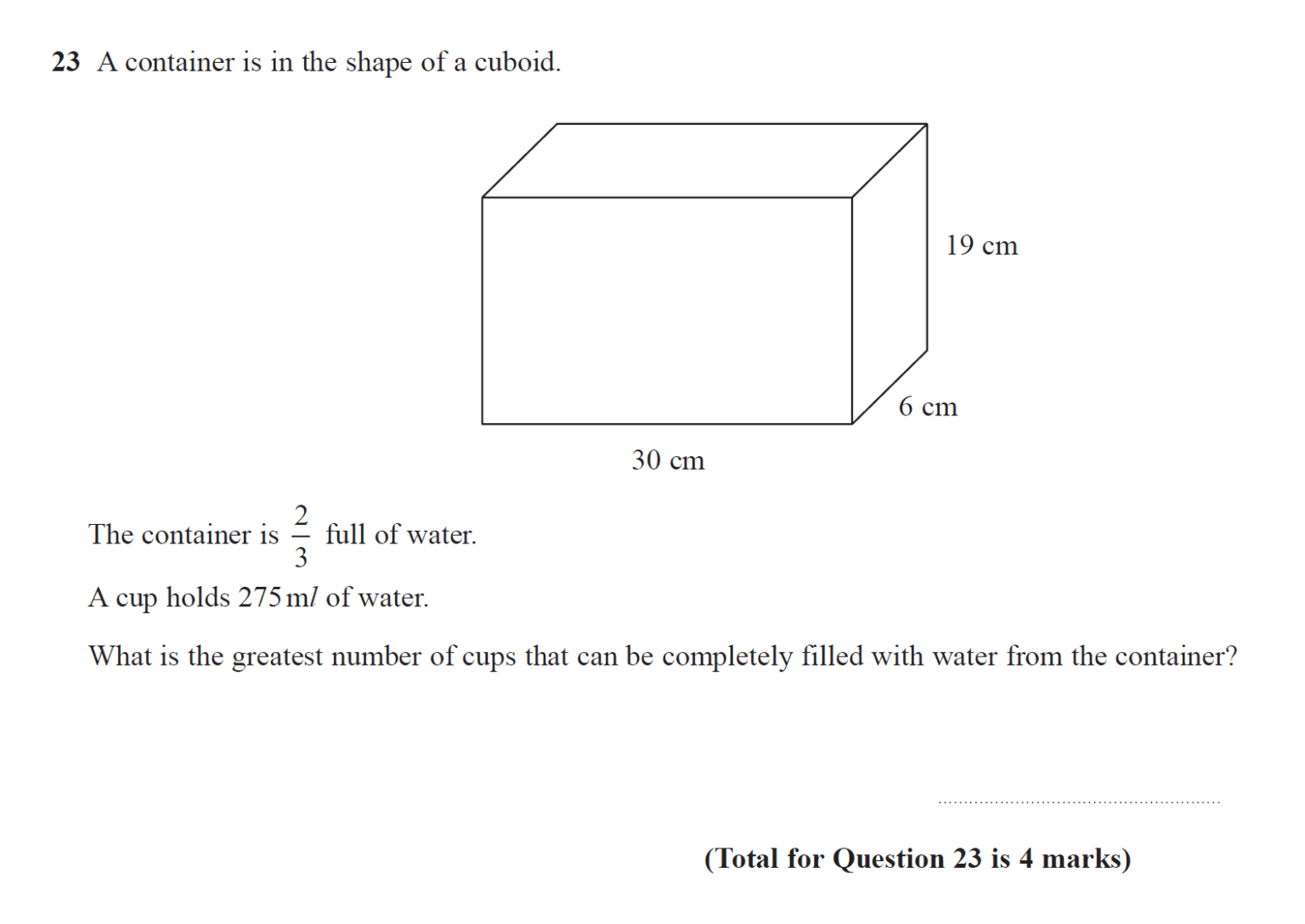
Calculating Volume

Volume measures the space inside a three-dimensional object. Here are the formulas:
Volume of Prisms

The volume (V) of a prism can be calculated as:
[ V = A \times h ]where (A) is the area of the base and (h) is the height.
Volume of Cylinders

Similarly, for cylinders, the volume formula is:
[ V = πr^2h ]where (r) is the radius of the base circle and (h) is the height of the cylinder.
Applying Prisms and Cylinders in Real Life

- Architecture: Architects use these calculations to estimate the amount of paint or plaster needed for building exteriors or interiors.
- Product Design: Volume calculations are essential in packaging to determine the size of containers like cans or boxes.
- Engineering: In mechanical engineering, understanding volumes helps in estimating material requirements for parts like engine cylinders or structural beams.
🏗️ Note: Accurate measurements are critical in construction to ensure material efficiency and structural integrity.
Mastering these Concepts

Here are some strategies to better understand and master these calculations:
- Visualize: Use physical models or visualization tools to understand the shape and its dimensions.
- Practice: Solve various problems to solidify your understanding of different scenarios involving prisms and cylinders.
- Use Formulas: Commit the surface area and volume formulas to memory and apply them consistently.
In this comprehensive guide, we've explored how to calculate the surface area and volume of prisms and cylinders, along with practical applications that highlight their significance. By mastering these calculations, you're not just learning mathematics but gaining skills that are indispensable in numerous professional fields. Remember, the key to mastering these concepts lies in practice, understanding the underlying principles, and applying them to real-world situations.
What is the difference between lateral area and total surface area?

+
The lateral area refers only to the sides or the curved surface of a prism or cylinder, whereas the total surface area includes both the lateral area and the area of the bases.
Can I calculate the volume of a cylinder if I only know its diameter and height?
+
Yes, you can! Convert the diameter to radius by dividing it by 2, then use the formula (V = πr^2h).
How do I visualize the volume of a complex prism?

+
Use 3D software or physical models to see how the different faces of the prism come together in space. This can help in visualizing how the base area extends to create the volume.



