Supplementary Angles And Complementary Angles Worksheet

Understanding Supplementary Angles and Complementary Angles
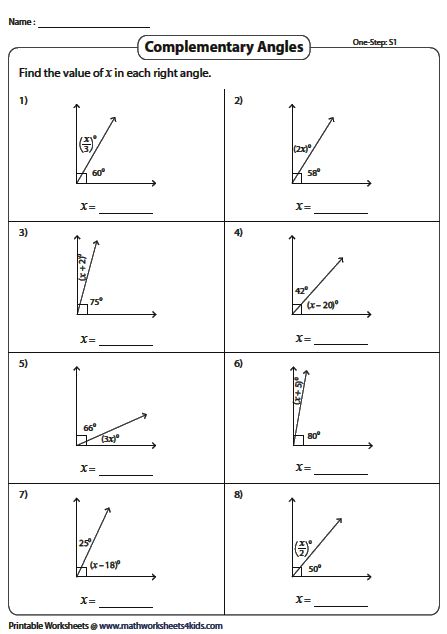
In the world of geometry, understanding the relationships between angles can unlock a deeper comprehension of shapes and space. Two particularly important concepts are supplementary angles and complementary angles. These terms might sound alike, but they refer to different angle relationships that have significant implications in the study of geometry and are often tested in various mathematical assessments. This post will delve into what these angles are, how they work together, and how to work through common problems involving them.
What are Supplementary Angles?

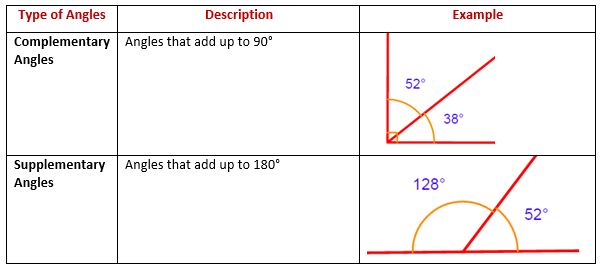
Supplementary angles are two angles whose measures add up to 180 degrees. When these angles are placed next to each other, they form a straight line. Here are the key characteristics:
- Two angles are supplementary if their sum is 180°.
- They do not have to be adjacent, but if they are, they form a linear pair (side-by-side).
- Supplementary angles can be anywhere on the plane, and the sum rule still applies.
Example

Imagine you have two angles, angle A and angle B, where angle A measures 120 degrees. To find the supplementary angle:
[ 180° - 120° = 60° ]
So, the supplementary angle to A is 60°.
What are Complementary Angles?

Complementary angles, on the other hand, are angles whose measures add up to 90 degrees. Here's how they work:
- Two angles are complementary if their sum is 90°.
- Like supplementary angles, they do not need to be adjacent, but if they are, they form a right angle.
- These angles are foundational in understanding the concept of right angles.
Example
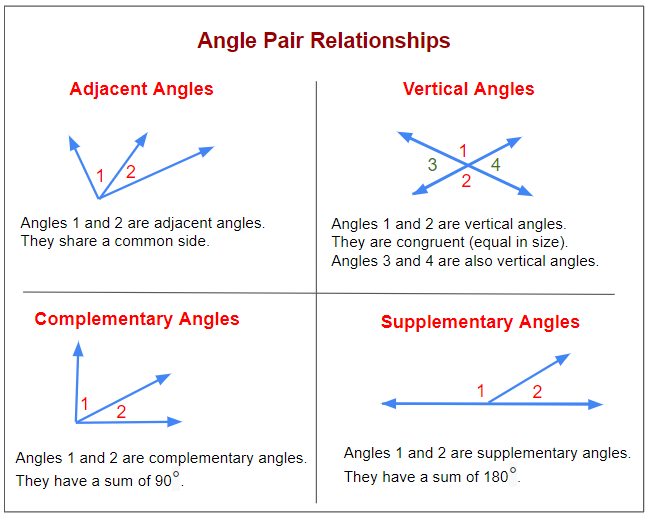
Consider angle C measuring 35 degrees. To find the complementary angle:
[ 90° - 35° = 55° ]
The complementary angle to C is 55°.
Worksheet: Identifying Supplementary and Complementary Angles

Here’s a worksheet to help practice identifying supplementary and complementary angles:
| Problem | Angle A | Angle B | Type of Angles | Answer |
|---|---|---|---|---|
| 1 | 45° | 135° | Supplementary | |
| 2 | 60° | 30° | Complementary | |
| 3 | 100° | 80° | Supplementary | |
| 4 | 45° | 45° | Both (either) |
✅ Note: The answers provided are examples. In actual problems, students would need to determine the correct type based on the given angles.
Steps for Solving Supplementary and Complementary Angles Problems

Here are the steps you might follow when dealing with these angles:
- Identify the sum: Determine if the sum of the angles is 90° or 180°.
- Find the missing angle: If one angle is given, subtract it from 90° (for complementary) or 180° (for supplementary).
- Check your work: Make sure your angles add up correctly.
Advanced Considerations

Here are some more advanced scenarios or considerations:
- Multiple angles: Sometimes, you might have more than two angles involved. You need to identify which pairs can be complementary or supplementary.
- Non-adjacent angles: Angles can be complementary or supplementary even if they are not adjacent or even on the same plane.
- Parallel lines and transversals: This is where supplementary angles play a crucial role in understanding corresponding, alternate, and co-interior angles.
Ultimately, understanding and applying supplementary and complementary angles not only helps in solving basic geometry problems but also enriches one's understanding of geometric theorems and proofs, which are fundamental in higher-level mathematics.
Final Thoughts

Supplementary and complementary angles are essential concepts in geometry that help us understand how angles interact within shapes and lines. Whether you're studying for an exam or just looking to deepen your knowledge of geometry, these concepts will prove to be invaluable. By practicing with worksheets, you can hone your ability to quickly identify these angle relationships, which can be particularly useful in more complex geometric proofs and problems. Remember, every angle is part of a bigger picture, and recognizing these relationships can simplify seemingly complex problems.
What’s the difference between complementary and supplementary angles?

+
Complementary angles add up to 90 degrees, while supplementary angles add up to 180 degrees.
Can supplementary angles be adjacent?

+
Yes, if two angles are supplementary and adjacent, they form a linear pair which makes a straight line.
How do you find a complementary angle if you know one angle?

+
Subtract the known angle from 90 degrees to find the complementary angle.
Are all right angles complementary?

+
Yes, because a right angle is 90 degrees, any angle paired with it will add up to 90 degrees, making them complementary.
Why are supplementary angles useful in geometry?

+
They are used to understand properties of straight lines, parallel lines, and in solving various geometric proofs involving angles.