5 Essential Tips for Mastering Supplementary and Congruent Angles

Understanding supplementary and congruent angles is a fundamental part of mastering geometry. These concepts not only appear frequently in mathematical problems but also play a crucial role in various real-world applications like architecture, engineering, and design. Whether you're a student looking to ace your next math exam or an enthusiast exploring the intricacies of geometry, these tips will help you gain a deeper understanding and excel in identifying, calculating, and applying supplementary and congruent angles effectively.
1. Understanding the Basics

Before diving into the more complex aspects of supplementary and congruent angles, let’s ensure we have a firm grasp on the basics:
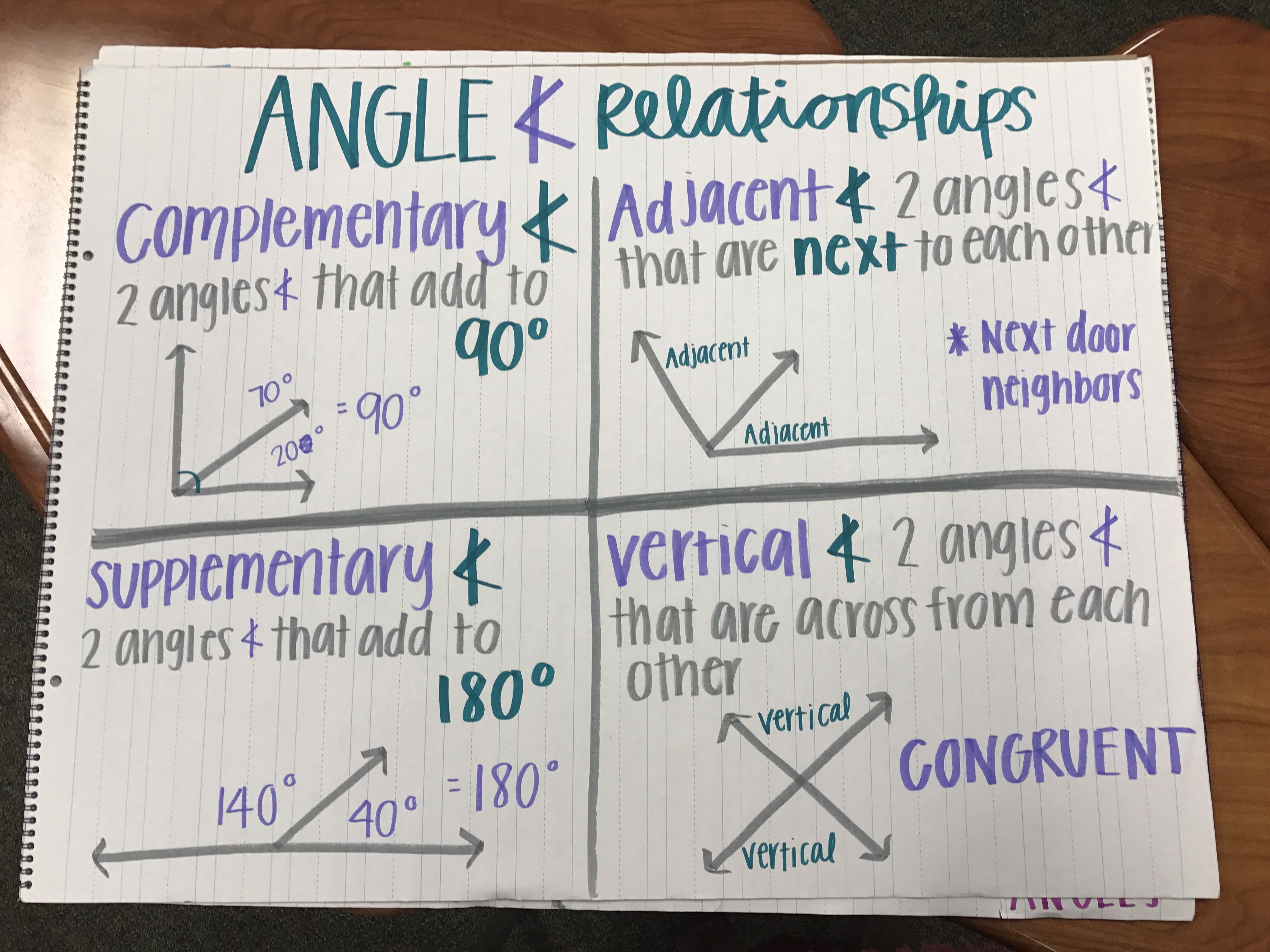
- Supplementary Angles: Two angles whose sum equals 180°. In other words, if you were to place one angle next to another, they would form a straight line.
- Congruent Angles: Angles that have the exact same measure. When two angles are congruent, their symbols are often marked with the same number of arcs.
How to Recognize Supplementary Angles

- These angles often appear in pairs where one angle can be deduced from knowing the other. For instance, if one angle is 60°, its supplementary angle will be 120°.
- They form a linear pair, which means they share a common side and vertex, and the non-common sides form a straight line.
Identifying Congruent Angles

- Congruent angles can be identified by looking for identical angle measures or through geometric theorems that imply congruence, like the Vertical Angles Theorem.
- In diagrams, congruent angles are often marked with matching arcs or colors.
📚 Note: Always remember that supplementary angles can be either adjacent or non-adjacent, but they must sum up to 180°.
2. Mastering Angle Calculations

To work effectively with supplementary and congruent angles, you need to be proficient in angle calculations:
- When given one angle of a supplementary pair, subtract this angle from 180° to find the other.
- If two angles are congruent, their measures are equal, so you can directly equate them in your calculations.
Here’s a quick formula for your toolkit:
| Angle Type | Calculation |
|---|---|
| Supplementary Angle | If angle A = x°, then Supplementary Angle = 180° - x° |
| Congruent Angles | If angle A = x° and angle B = x°, then A = B |

🧮 Note: When dealing with real-world problems or complex diagrams, remember to consider angles formed by intersecting lines or parallel lines cut by a transversal.
3. Applying Theorems and Properties

Geometry is rich with theorems that help in understanding the relationships between angles:
- Vertical Angles Theorem: Vertical (or opposite) angles formed by two intersecting lines are congruent.
- Angles on a Straight Line: Any angles on a straight line add up to 180°, which is essential for identifying supplementary angles.
- Alternate Interior and Corresponding Angles: When parallel lines are cut by a transversal, these angles are congruent or supplementary, depending on their position.
Example in Use

Consider parallel lines l and m with a transversal t intersecting them. If ∠1 and ∠2 are alternate interior angles, then ∠1 = ∠2. Also, ∠1 and ∠3 (a pair of corresponding angles) are congruent, while ∠1 and ∠4 (a pair of consecutive interior angles) are supplementary.
🔍 Note: Recognizing and utilizing these properties can significantly simplify solving for unknown angles in various geometric configurations.
4. Visual Identification and Diagrams

Geometry is a highly visual field, and understanding angles often involves interpreting diagrams correctly:
- Look for common geometric shapes or angles formed by lines or curves.
- Use diagrams to confirm your calculations by visualizing the angles and how they interact.
Practice with Diagrams

Create or find diagrams where you identify supplementary and congruent angles. This practice will sharpen your ability to:
- Recognize the position and relationships of angles in complex diagrams.
- Understand how different geometric configurations affect angle relationships.
🎨 Note: Diagrams are not just tools for problem solving but also for mastering conceptual understanding.
5. Continuous Problem Solving

Like any skill, proficiency in geometry comes with practice:
- Solve problems from textbooks, online resources, or past exams focusing on supplementary and congruent angles.
- Explain your steps aloud or to someone else to reinforce your understanding.
- Work on problems where you need to apply more than one theorem or property at a time to solve for angles.
Here are some problem-solving strategies:
- Start with what you know and work backward to find unknown angles.
- Use the process of elimination in multiple-choice questions to narrow down answers.
- Draw auxiliary lines or mark congruent angles with arcs to visualize the problem better.
💡 Note: Real-world problems often require you to integrate various geometric principles, not just focusing on angles alone.
In summary, mastering supplementary and congruent angles involves a blend of theoretical understanding and practical application. By mastering the basics, practicing calculations, understanding geometric properties, enhancing visual recognition, and engaging in continuous problem-solving, you can tackle any angle-related challenge in geometry with confidence. This journey through the world of angles not only sharpens your mathematical acumen but also prepares you for fields where precision in spatial understanding is paramount.
What is the difference between supplementary and complementary angles?

+
Supplementary angles add up to 180°, forming a straight line, while complementary angles add up to 90°, forming a right angle. While supplementary angles can be adjacent or non-adjacent, complementary angles are usually adjacent.
How can I identify congruent angles in diagrams?

+
Look for marks indicating congruence like arcs, ticks, or labels. Additionally, congruent angles can be inferred from theorems like vertical angles or when corresponding or alternate interior angles are formed by parallel lines and transversals.
Are all angles that form a straight line supplementary?
+
Yes, any pair of angles that together form a straight line are supplementary because their sum is 180°.
Can an angle be both supplementary and congruent to another angle?

+
Yes, but only if both angles are 90°. In this special case, they would both be complementary and supplementary because 90° + 90° = 180°.
What are some common mistakes to avoid when dealing with angles?

+
One common mistake is not recognizing when angles are supplementary rather than complementary, or mistaking congruent angles for supplementary ones due to confusion over their positioning. Also, overlooking vertical angles as congruent or not considering angles formed by transversals intersecting parallel lines can lead to errors.