Mastering Supplementary & Complementary Angles: Fun Worksheet

Understanding supplementary and complementary angles is fundamental in mastering the basics of geometry. These concepts not only appear in academic tests but also in real-life scenarios, from engineering design to artistic composition. In this comprehensive blog post, we will delve into these angles, offering educational insights, practical examples, and fun ways to practice with worksheets.
What Are Supplementary and Complementary Angles?

Let’s start with the definitions:
- Complementary Angles: Two angles whose measures add up to 90 degrees. For instance, if you have an angle of 30 degrees, its complementary angle would be 60 degrees because 30 + 60 = 90.
- Supplementary Angles: Two angles whose measures add up to 180 degrees. For example, if one angle measures 135 degrees, its supplementary angle would be 45 degrees because 135 + 45 = 180.

Why Are They Important?

Understanding these types of angles can:
- Enhance problem-solving skills in geometry.
- Provide practical application in areas like architecture, where angles must be calculated accurately.
- Foster an intuitive understanding of how angles relate in space.
How to Identify and Calculate?

Here are some simple steps:
- Identify the given angle: Start by noting the angle you have.
- Find the complement: For a complementary angle, subtract the given angle from 90 degrees.
- Find the supplement: For a supplementary angle, subtract the given angle from 180 degrees.
Practical Examples

Let’s look at some practical examples to illustrate these concepts:
Example 1: Complementary Angles in Art

Imagine an artist painting a seascape where the horizon line forms a 40-degree angle with the horizontal:
- The angle between the horizon and the sky would be its complement, or 50 degrees (90 - 40).
Example 2: Supplementary Angles in Design

When designing a bridge, engineers ensure that the angles at certain joints add up to 180 degrees:
- If one angle at a joint is 120 degrees, the supplementary angle at the other end must be 60 degrees (180 - 120).
Fun Worksheet to Practice
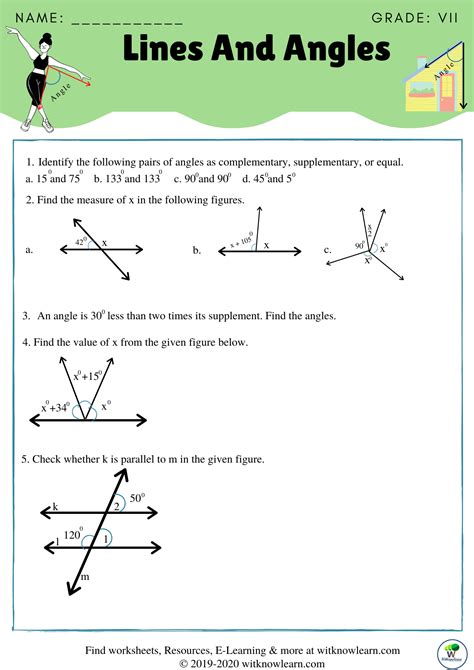
To help you or your students practice these concepts, we’ve created an interactive worksheet. Here’s how to use it:
| Angle Given | Find Complementary | Find Supplementary |
|---|---|---|
| 25° | ||
| 150° | ||
| 30° | ||
| 75° |

🔍 Note: Fill in the blank cells with the appropriate complementary or supplementary angles. This worksheet is designed to be both educational and engaging.
Tips for Teaching and Learning

Here are some strategies to master these angles:
- Use visual aids: Tools like protractors and angle rulers are invaluable in visualizing angles.
- Real-life application: Connect theoretical knowledge with practical examples, such as in carpentry or sports.
- Encourage interactive learning: Group activities or educational games can make learning fun and competitive.
As we wrap up our exploration of supplementary and complementary angles, we can see that these concepts are not just academic exercises but integral parts of our everyday interaction with the world around us. They help us in designing, analyzing, and appreciating the geometry in life. Understanding these angles equips learners with a foundational skill that transcends the classroom, applying to real-life scenarios where angles matter.
What’s the difference between supplementary and complementary angles?

+
Supplementary angles add up to 180 degrees, whereas complementary angles add up to 90 degrees.
How can I remember which is which?

+
Use mnemonics like “C for complementary comes before S for supplementary in the alphabet, and C angles are less than S angles (90<180)."
Are there angles that are both supplementary and complementary?

+
No, an angle cannot be both supplementary and complementary because 90 degrees (complementary) is not enough to make 180 degrees (supplementary).