Super Teacher Worksheets Equivalent Fractions Answer Key
Teaching equivalent fractions can be quite the challenge, but with the right resources, it becomes an engaging and straightforward process. Super Teacher Worksheets offers an array of tools designed to make learning fractions fun and accessible for students of various ages. One such tool is the Equivalent Fractions Worksheet Answer Key, which simplifies the teaching and learning experience by providing clear, visual aids and straightforward answers to ensure students grasp the concept effectively.
Understanding Equivalent Fractions

Equivalent fractions are different fractions that represent the same part of a whole. They might look different due to differing numerators and denominators, but their value remains the same when reduced to their simplest form. This foundational concept in fractions is crucial for:
- Simplifying fractions
- Comparing fractions
- Adding and subtracting fractions with unlike denominators
Here are steps to teach equivalent fractions using Super Teacher Worksheets:
Visual and Interactive Learning

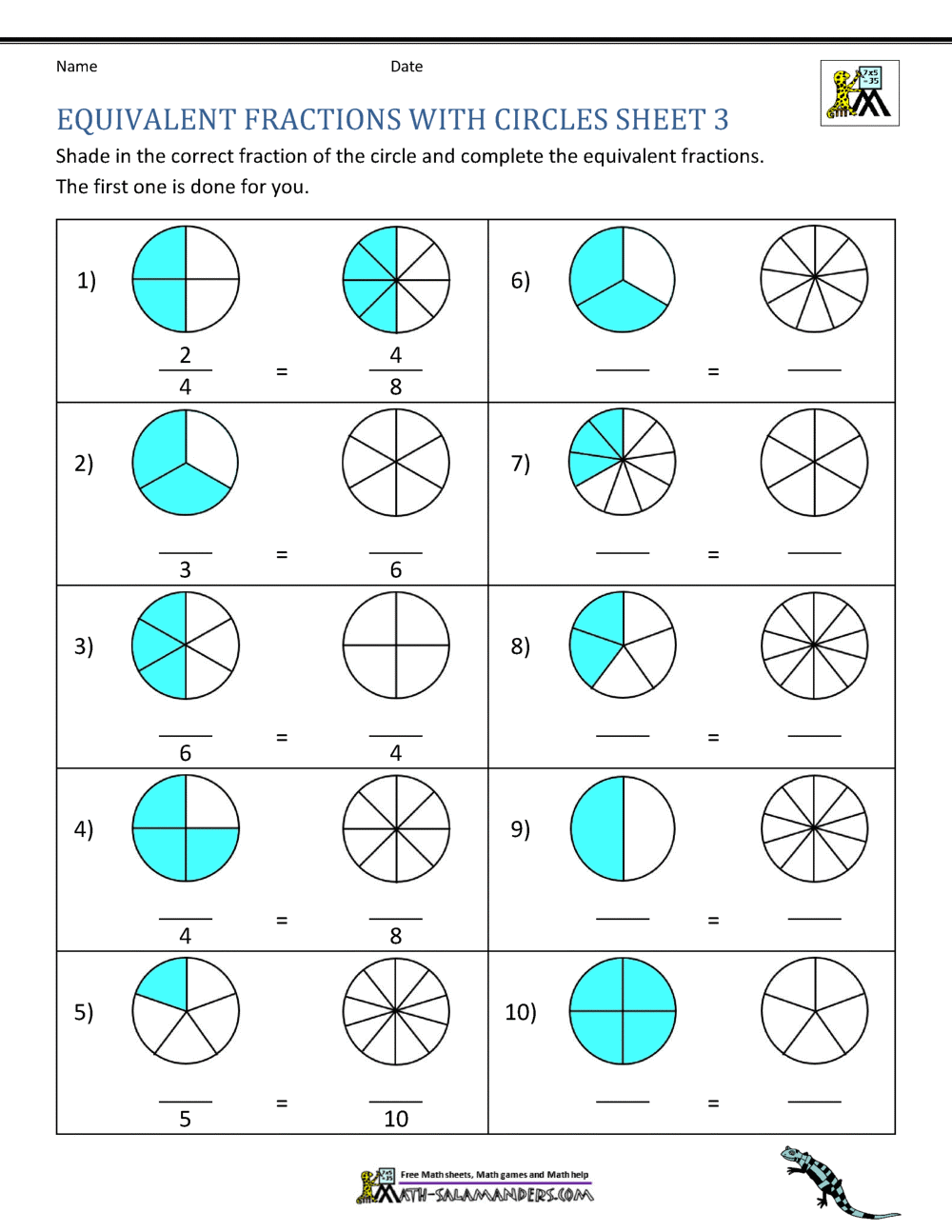
Super Teacher Worksheets uses visual aids like:
- Shapes divided into equal parts to represent fractions
- Number lines
- Pizza slice diagrams
Example: To show that (\frac{1}{2}) is equivalent to (\frac{2}{4}), the worksheet might use a pizza divided into four slices with two slices shaded. This visual representation makes it clear that both fractions represent the same amount.
🌟 Note: Visual learning is key for younger students to understand abstract concepts like fractions.
Practice Worksheets

The worksheets provide numerous examples for students to practice finding equivalent fractions:
- Matching problems: Students match equivalent pairs from given fractions
- Conversions: Changing a given fraction to an equivalent one with different numerators and denominators
- Simple exercises: Filling in blanks with fractions that are equivalent to the given ones
These exercises are designed to ensure students understand:
- The multiplication and division properties of fractions
- How to find common denominators
Answer Key

The accompanying Answer Key provides:
| Problem | Solution |
|---|---|
| Find an equivalent fraction to (\frac{3}{6}) | (\frac{1}{2}) |
| Convert (\frac{1}{4}) to an equivalent fraction with 20 as the denominator | (\frac{5}{20}) |
| Match the equivalent fractions (\frac{2}{3}), (\frac{4}{6}), (\frac{6}{9}) | All are equivalent |

With these answers, teachers can:
- Quickly check student work for accuracy
- Ensure correct methodologies are being followed
- Guide students through common mistakes
Reinforcement Through Real-World Examples

Super Teacher Worksheets also includes real-world application exercises:
- Cooking fractions (e.g., half, quarter recipes)
- Measurement conversion (e.g., inches to feet, ounces to pounds)
- Pizza sharing (e.g., distributing slices among friends)
These scenarios help students see the relevance and practicality of equivalent fractions in everyday life.
Progressive Learning
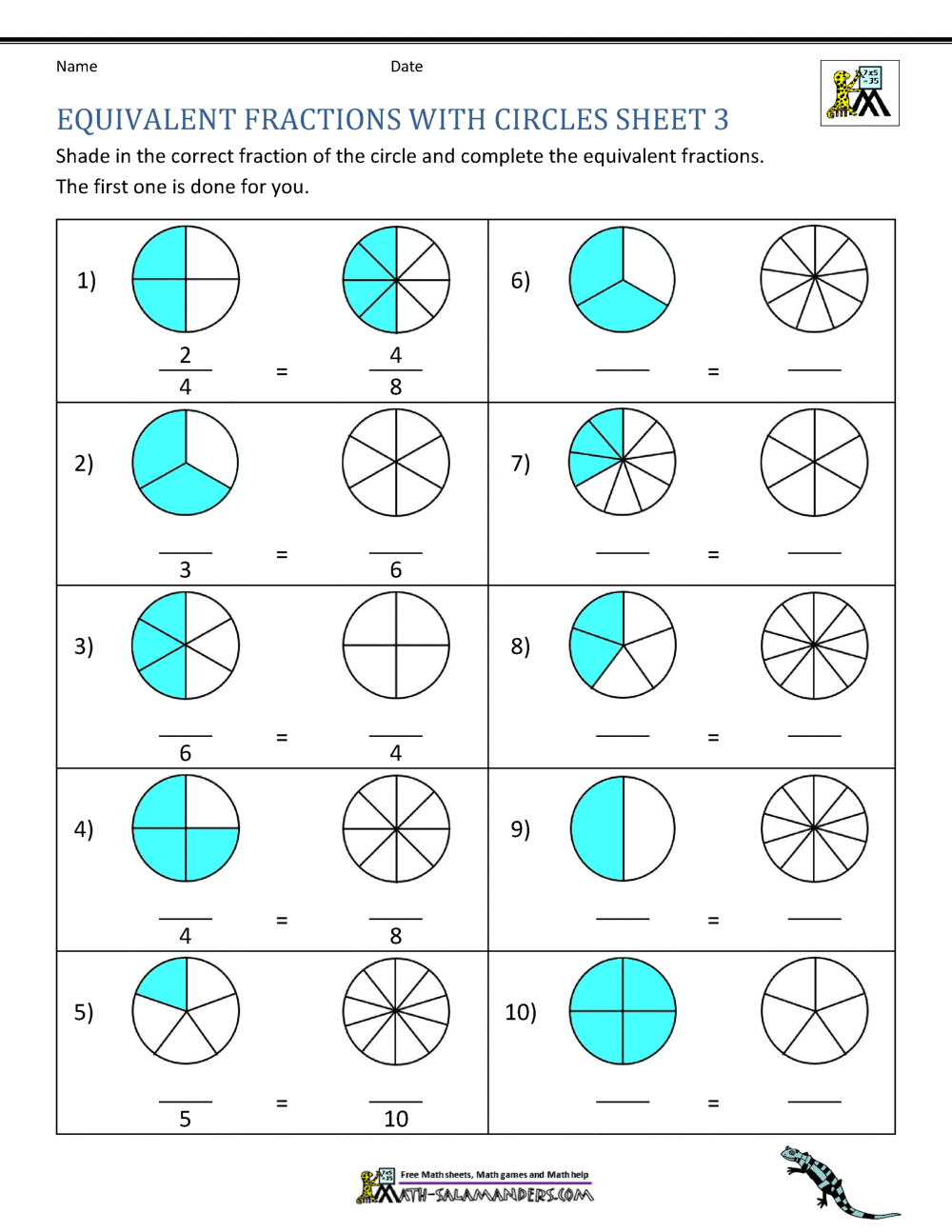
The worksheets come with:
- Step-by-step instructions for solving problems
- Difficulty progression from basic to complex fractions
- Immediate feedback with answer keys
This approach promotes:
- Independence in learning
- Confidence through understanding
- Mastery of the topic
Using Super Teacher Worksheets' resources, teachers can effectively guide students to understand and apply equivalent fractions, ensuring they not only memorize the answers but comprehend the underlying principles. The diverse tools from simple explanations to real-world examples help in creating a solid foundation for further fraction-based learning.
In wrapping up, the use of Super Teacher Worksheets, especially the Equivalent Fractions Answer Key, has proven invaluable in demystifying equivalent fractions for students. By incorporating visual learning, step-by-step problem-solving, and real-life scenarios, these worksheets facilitate a holistic understanding of fractions, enabling students to excel in math and related subjects.
How do I know if two fractions are equivalent?

+
To check if two fractions are equivalent, you can multiply or divide both the numerator and the denominator of one fraction by the same number to see if it matches the other. If they simplify to the same value, they are equivalent.
What are common mistakes students make with equivalent fractions?

+
Students often forget to multiply or divide both the numerator and the denominator by the same number, leading to incorrect equivalent fractions. They might also struggle with understanding how changing the denominator affects the fraction’s value.
Can equivalent fractions help in comparing fractions?

+
Absolutely. Finding equivalent fractions with a common denominator is a key strategy for comparing fractions. By converting both fractions to have the same denominator, it becomes much easier to determine which one is larger or smaller.



