Subtraction Fractions Worksheets

Fractions are a fundamental concept in mathematics that permeate numerous practical applications in real life, from cooking recipes to measurements in construction and financial transactions. An understanding of fractions and operations with fractions, such as subtraction, is essential for developing a strong foundation in mathematics. In this comprehensive blog post, we dive deep into the intricacies of subtracting fractions, providing you with the knowledge and tools you need through Subtraction Fractions Worksheets. Whether you're a student, teacher, or simply someone interested in refreshing your math skills, this guide will walk you through the steps, offer insights, and provide practice to master fraction subtraction.
Understanding Fractions


Before we delve into subtracting fractions, it’s crucial to have a firm grasp of what fractions are:
- Numerator: The top number of a fraction that tells you how many parts you have.
- Denominator: The bottom number that indicates the total number of equal parts in the whole or the group.
Fractions can be thought of as slices of pie, portions of a bar, or segments of a timeline, helping visualize the division of a whole into equal parts.
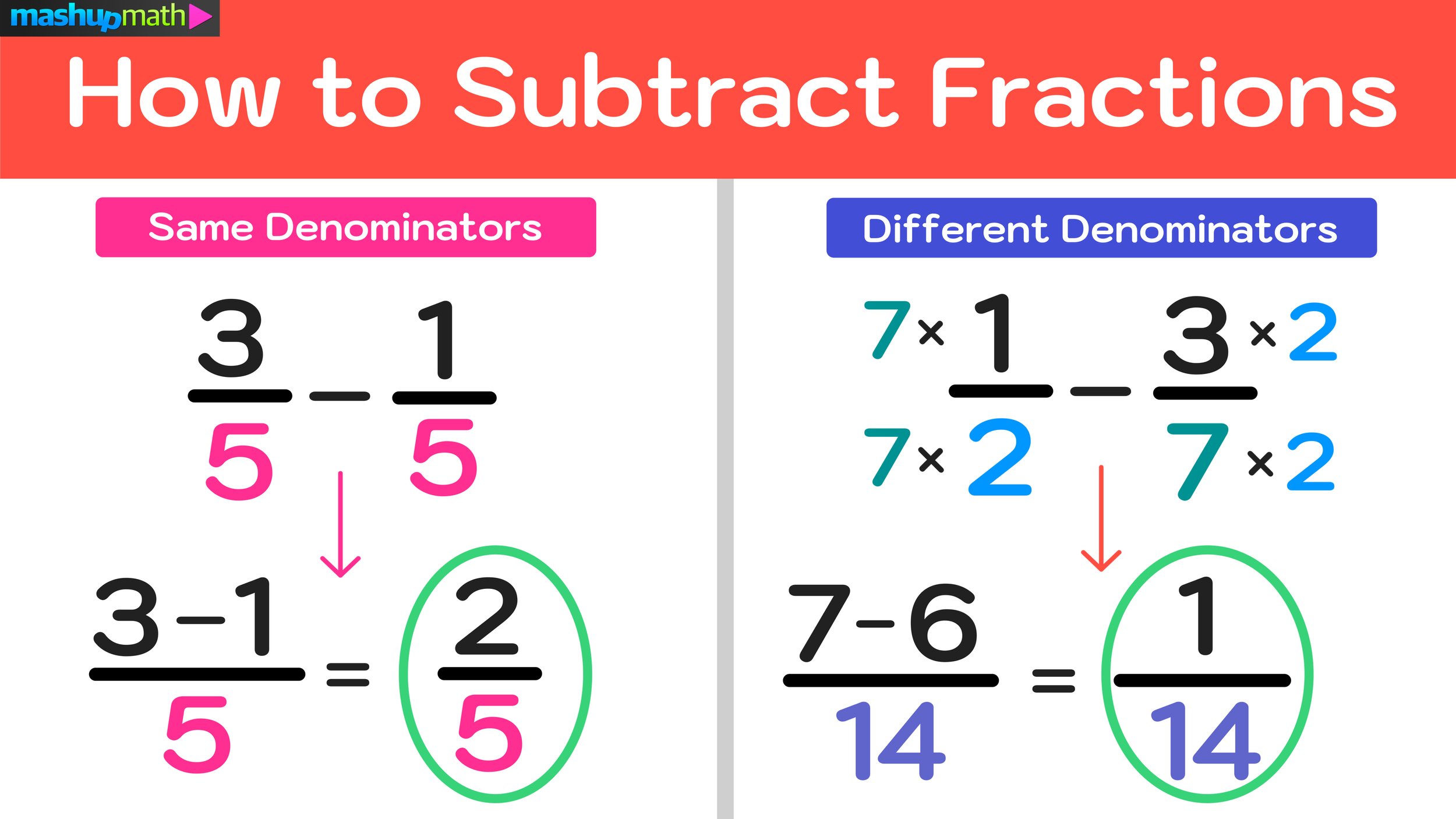
The Basics of Subtracting Fractions

Subtracting fractions might seem daunting at first, but the process is quite straightforward once you know the rules:
- Find a Common Denominator: Ensure both fractions have the same denominator. If they don’t, you’ll need to find a common denominator.
- Convert Numerator: Adjust the numerators so the fractions represent the same value with the common denominator.
- Perform Subtraction: Subtract the numerators, keeping the denominator the same.
- Simplify if Possible: Reduce the resulting fraction to its simplest form.
Finding a Common Denominator

| Fraction 1 | Fraction 2 | Common Denominator |
|---|---|---|
| 1⁄3 | 1⁄4 | 12 |
| 3⁄5 | 2⁄3 | 15 |

The common denominator is the least common multiple (LCM) of the given denominators. Here are some methods:
- Listing Multiples
- Using the Least Common Multiple (LCM) formula
- Prime Factorization
Once you’ve found the common denominator, convert both fractions:
[ \frac{a}{b} - \frac{c}{d} = \frac{a \cdot m}{b \cdot m} - \frac{c \cdot n}{d \cdot n} ] where (m) and (n) make the denominators equal.
Performing the Subtraction

Now, subtract the numerators:
[ \frac{a \cdot m}{b \cdot m} - \frac{c \cdot n}{d \cdot n} = \frac{a \cdot m - c \cdot n}{b \cdot m} ]
Simplifying the Fraction

After subtracting, if possible, simplify the fraction by dividing the numerator and denominator by their greatest common divisor (GCD).
🔍 Note: Ensure you simplify fractions to their simplest form to make your answer clear and professional.
Using Subtraction Fractions Worksheets


To enhance your understanding and proficiency in subtracting fractions, worksheets are an invaluable resource:
- Visual Aids: Worksheets often include diagrams to help visualize the fractions and the subtraction process.
- Practice Problems: They provide a range of problems from simple to complex, allowing you to test and improve your skills.
- Step-by-Step: Some worksheets guide you through each step, reinforcing learning.
The following table provides an overview of the types of worksheets available:
| Type | Description | Skill Level |
|---|---|---|
| Basic Subtraction | Simple like-denominator problems | Beginner |
| Complex Subtraction | Involves finding common denominators | Intermediate |
| Mixed Numbers | Deals with subtracting mixed numbers and fractions | Advanced |
Choose the right worksheet based on your skill level to get the most out of your practice:
Advantages of Worksheets
- Repetition: Regular practice helps solidify the concept.
- Confidence Building: As you solve more problems, your confidence grows.
- Structured Learning: Worksheets provide a roadmap for learning, ensuring all aspects are covered.
In summary, this blog post has covered the fundamentals of subtracting fractions. We began by understanding fractions, moved on to the step-by-step process of subtracting them, and emphasized the importance of finding common denominators. We explored how subtraction fractions worksheets can be instrumental in mastering this skill, offering structured practice and visual aids. Remember, consistent practice with these worksheets not only reinforces the process but also helps in retaining the knowledge for practical applications. Keep practicing, and soon, subtracting fractions will become second nature!
Why is finding a common denominator necessary when subtracting fractions?

+
A common denominator allows you to ensure both fractions have equal parts or units when performing the subtraction, making the operation meaningful and accurate.
Can I subtract fractions with different denominators directly?

+
No, you must convert them to have a common denominator first to ensure you’re subtracting the same type of fraction unit.
How do I know which common denominator to choose?

+
The smallest common denominator is usually preferred. This is the Least Common Multiple (LCM) of the given denominators, which simplifies the subsequent steps in the subtraction process.