Standard Form to Slope Intercept: Easy Conversion Tips

Converting equations from standard form to slope-intercept form can sometimes seem like a challenging task, especially for those new to algebra. However, understanding this conversion is crucial for graphing lines, solving linear equations, and various other mathematical applications. This guide provides step-by-step instructions to make this process straightforward and easy to understand, ensuring that you can grasp and apply these concepts with confidence.
Understanding the Two Forms

Before delving into the conversion process, let’s first clarify what we mean by standard form and slope-intercept form:
- Standard Form: Ax + By = C, where A, B, and C are constants, and A must be non-negative (if it isn’t, we can multiply the entire equation by -1).
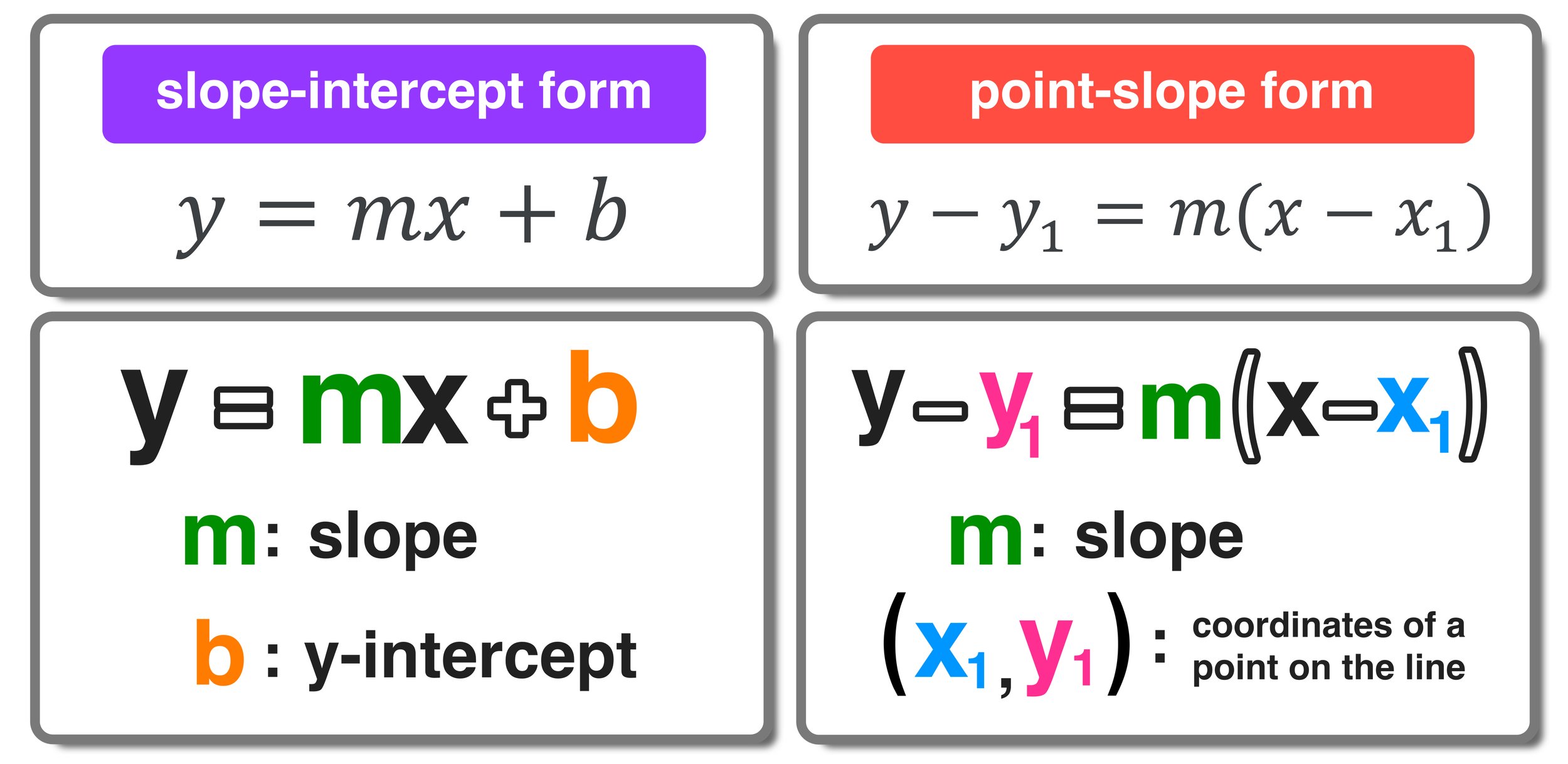
- Slope-Intercept Form: y = mx + b, where m represents the slope and b represents the y-intercept.
Conversion Steps

To convert from standard form to slope-intercept form, follow these steps:
1. Isolate y

Your goal is to have y by itself on one side of the equation.
- If the equation isn’t already in standard form, rearrange it to fit Ax + By = C.
- Move the x-term to the other side by subtracting Ax from both sides. You’ll get:
- By = -Ax + C
- Now, divide every term by B (assuming B is not zero) to isolate y:
- y = (-A/B)x + (C/B)
2. Identify Slope and y-Intercept

- The coefficient of x (-A/B) is the slope m.
- The constant term (C/B) is the y-intercept b.
Example:

Let’s convert the equation 2x + 3y = 6 to slope-intercept form:
- Subtract 2x from both sides:
- 3y = -2x + 6
- Divide each term by 3:
- y = (-2⁄3)x + 2
Now, we see that the slope m is -2⁄3 and the y-intercept b is 2.
📝 Note: If A or B is negative in the original equation, the sign will change when isolating y, but remember to include that change in your final slope.
When B = 0

If B equals zero, the equation simplifies to Ax = C. Here, there is no y-term, which means the line is vertical and cannot be expressed in slope-intercept form. The equation represents a vertical line with x = C/B, or simply x = C/A where A is not zero.
Handling Fractional Slopes
When you end up with a fractional slope, especially after dividing by B, ensure you simplify the fraction if possible. For instance, if you find (-3⁄4) after division, simplify it to -3⁄4 or -0.75.
| Standard Form | Slope-Intercept Form | Slope (m) | y-Intercept (b) |
|---|---|---|---|
| 3x + 2y = 6 | y = (-3/2)x + 3 | -3/2 | 3 |
| -x + y = 5 | y = x + 5 | 1 | 5 |
| 4x - 2y = 8 | y = 2x - 4 | 2 | -4 |

Converting from standard form to slope-intercept form involves a simple rearrangement of terms, but understanding the process deeply enhances one's ability to work with linear equations effectively. It's not just about moving numbers around; it's about seeing the relationship between different forms of the same equation, which can provide insights into graphing, parallel and perpendicular lines, and solving systems of equations.
In your mathematical journey, this conversion will come in handy, allowing you to quickly identify how a line behaves on a graph without calculating or drawing it. The slope-intercept form provides a clear visual interpretation of a line's characteristics, making graphing and analysis straightforward.
📝 Note: Remember, this conversion works best when B is not zero. If B is zero, you're dealing with a vertical line, which has an undefined slope and can't be converted to slope-intercept form.
Lastly, this skill is not only useful in academic settings but also in various real-world scenarios where understanding line behavior, like in financial modeling or physics calculations, can be crucial.
Why do we need to convert from standard form to slope-intercept form?

+
Converting to slope-intercept form (y = mx + b) gives you immediate insight into the line’s slope (m) and y-intercept (b), making graphing and analysis much easier. It’s particularly useful for visualizing how the line behaves or determining if two lines are parallel or perpendicular based on their slopes.
What if I can’t isolate y?

+
If you can’t isolate y, it might mean the equation represents a vertical line or there’s no y-term (B=0). In such cases, the line cannot be expressed in slope-intercept form because its slope is undefined.
Can I use this conversion for graphing?

+
Absolutely! Slope-intercept form gives you all the necessary information to plot a line quickly. The slope tells you the rise over run, and the y-intercept tells you where the line crosses the y-axis.



