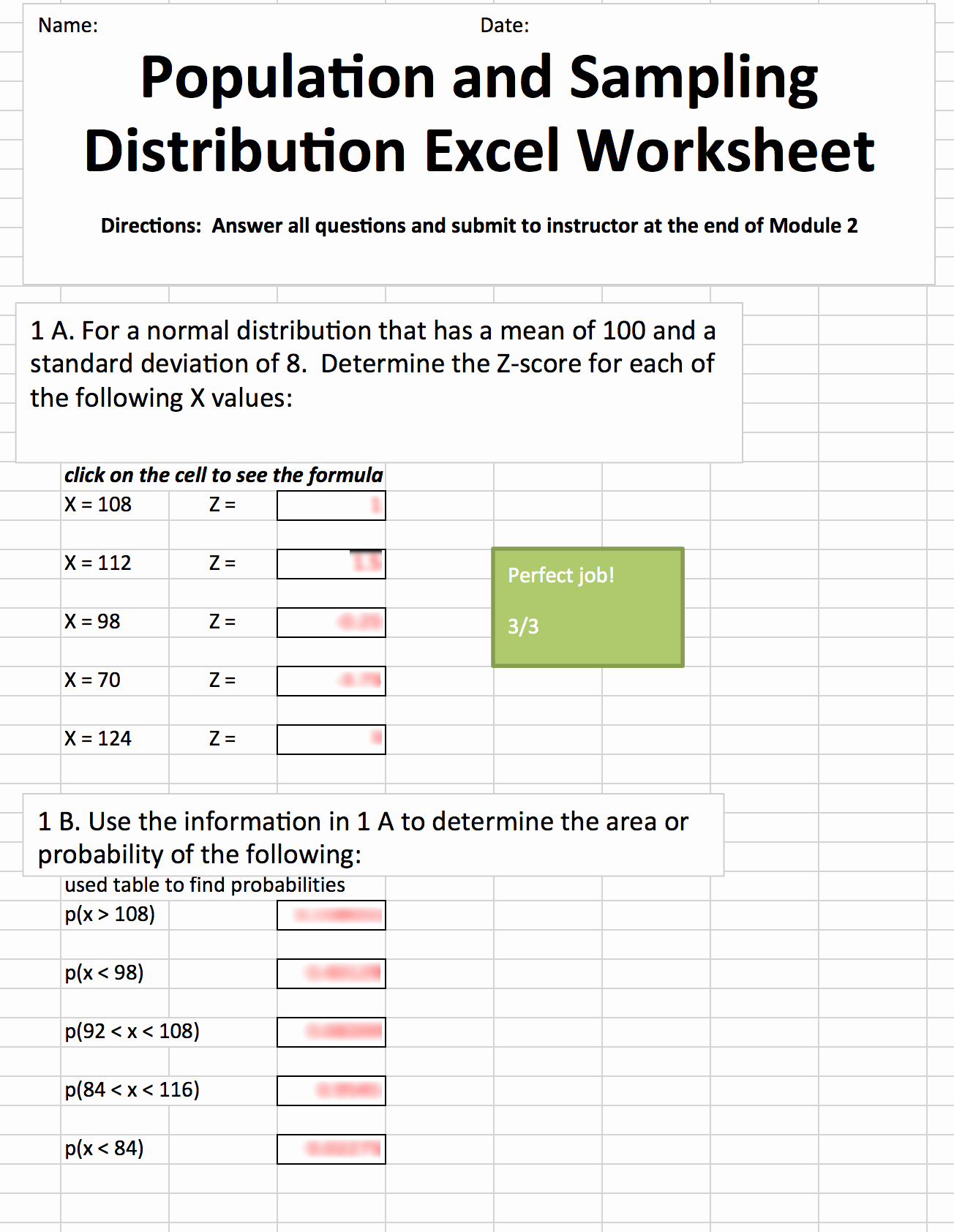
Standard Deviation Worksheet: 5 Easy Solutions

Statistics can often be a daunting subject for many students, and one of the key concepts they encounter is the standard deviation. It's a measure that tells us how spread out the numbers in a data set are from the mean. Understanding and calculating standard deviation is crucial for analyzing data in fields ranging from finance to psychology. This post will walk you through five straightforward methods to calculate and understand standard deviation with examples and step-by-step guides.
What is Standard Deviation?

Standard deviation (SD) is a statistical measure that quantifies the amount of variation or dispersion in a set of data values. A low standard deviation indicates that the values tend to be close to the mean of the set, while a high standard deviation indicates that the values are spread out over a wider range.
Why is Standard Deviation Important?
- Risk Analysis: It’s used to measure the volatility of returns in investments.
- Quality Control: Ensures products or services are consistent with minimal variability.
- Psychometrics: Helps in understanding the reliability of psychological tests.
- Weather Forecasting: Gauges the uncertainty of weather predictions.
Method 1: Manual Calculation

Here’s how you can calculate standard deviation by hand:
- Calculate the Mean: Add all the numbers together and divide by the number of items in your data set.
- Deviation from the Mean: Subtract the mean from each data point, then square each result.
- Mean of Squared Deviations: Sum the squared deviations and divide by the number of data points minus one.
- Take the Square Root: Find the square root of the result to get the standard deviation.
📝 Note: For sample standard deviation (used when you're not looking at the entire population), divide by n-1. For population standard deviation, use n in step 3.
Method 2: Using a Calculator

Many scientific and statistical calculators have a built-in function to calculate standard deviation:
- Enter the data points into the calculator.
- Press the button labeled SD or σ (sigma), often located under the STAT mode.
- Your calculator will display the standard deviation for you.
📝 Note: Make sure to use the correct mode for either sample or population standard deviation.
Method 3: Spreadsheet Software

Excel, Google Sheets, and similar software provide a straightforward way to compute standard deviation:
- Enter your data in a column or row.
- Use the function
=STDEV.S(array)for sample standard deviation or=STDEV.P(array)for population standard deviation.
📝 Note: STDEV.S calculates the sample standard deviation; use STDEV.P when you have the entire population.
Method 4: Online Calculators

There are numerous online tools available for calculating standard deviation:
- Search for “standard deviation calculator” on any search engine.
- Enter your data set as instructed on the tool.
- Click calculate or submit to view the results.
📝 Note: Verify that the online calculator you use specifies whether it's for sample or population standard deviation.
Method 5: Using Statistical Software

Advanced tools like R, Python (with libraries like NumPy, SciPy), and SPSS can handle complex statistical analyses:
- R: Use the
sd()function from the base package. - Python: Use
numpy.std()with the appropriate axis and ddof parameters. - SPSS: Select Descriptive Statistics under the Analyze menu.
📝 Note: Ensure you have the correct data type, and for sample data, remember to set ddof=1 in Python's NumPy for sample standard deviation.
Applying Standard Deviation in Real World Scenarios

Let’s look at a simple table demonstrating the application of standard deviation in a real-world context:
| Data Set | Mean | Standard Deviation |
|---|---|---|
| Student Test Scores | 75 | 12 |
| Annual Salaries | 60,000</td> <td>5,000 | |
| Temperature Readings | 22°C | 3°C |
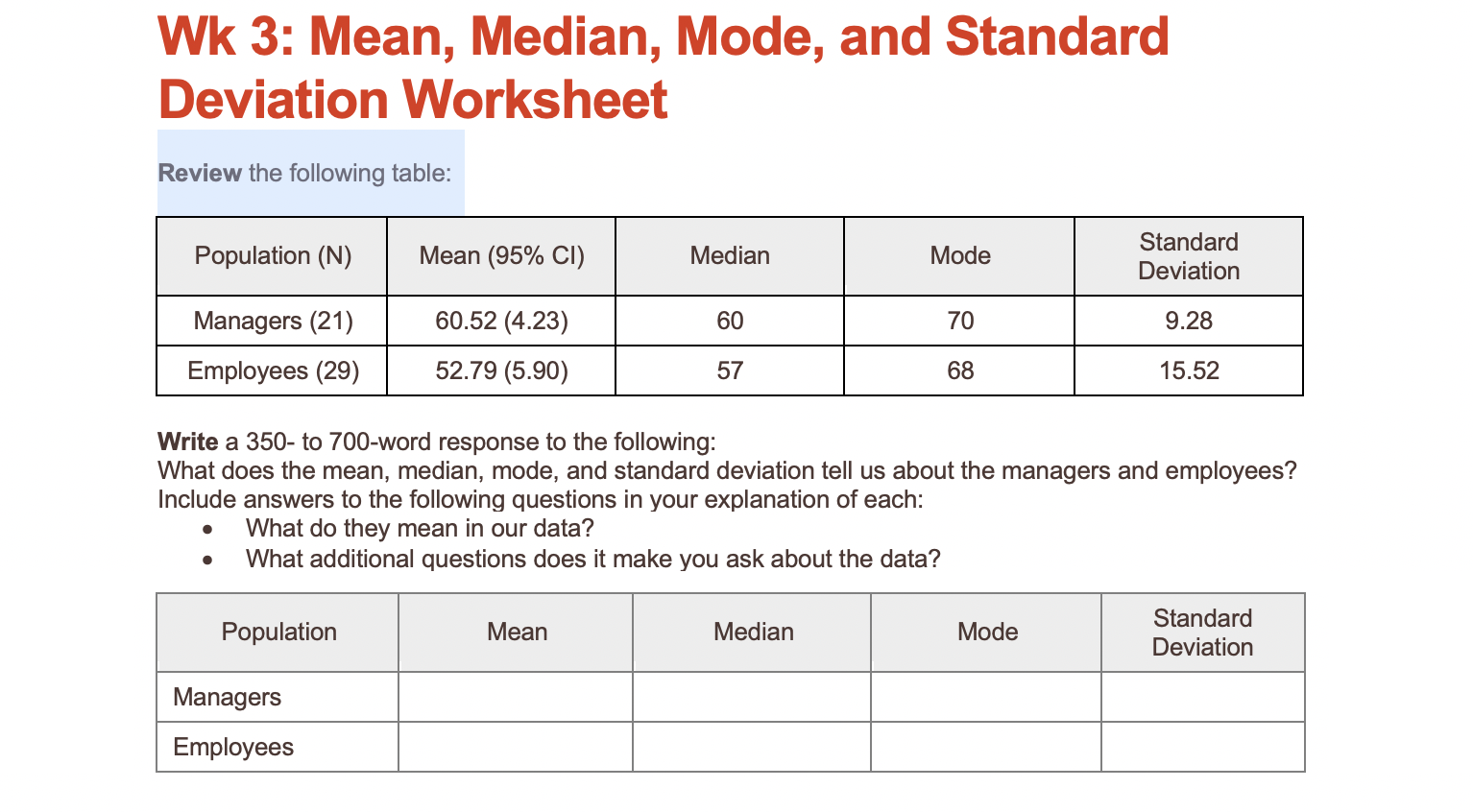
In this example, we can infer that student test scores have a moderate spread around the mean score, suggesting that student performance varies quite a bit. Annual salaries, on the other hand, show less variability, implying a more consistent salary range. Lastly, temperature readings indicate a narrow range of variation, typical of stable weather conditions.
Standard deviation is not just a theoretical tool but has practical applications across many fields. It helps in interpreting the variability within a dataset, which is essential for making informed decisions based on data analysis. Each method outlined here provides different levels of ease and complexity, catering to various needs from manual calculations to high-powered software solutions.
What is the difference between sample and population standard deviation?

+
Sample standard deviation uses n-1 in the denominator for calculation, making it slightly higher than population standard deviation, which uses n. This is called Bessel's correction.
Can standard deviation ever be negative?

+
No, standard deviation is always non-negative because it involves squaring the deviations, which removes any negative signs.
What if my dataset has outliers?

+
Outliers can significantly affect the standard deviation, causing it to be misleadingly large. Consider using methods like the interquartile range for such datasets or investigate why the outliers exist.
Why is the standard deviation useful in finance?

+
It's used to measure the risk associated with investment returns. A higher standard deviation indicates higher volatility or risk.
To summarize, mastering standard deviation calculation enhances your ability to analyze and interpret data effectively. By understanding the variability within your datasets, you can make more informed decisions in various fields, from business analytics to scientific research. Whether you’re a student struggling with statistics or a professional needing to analyze data, these methods provide you with tools to tackle standard deviation confidently.