Unlocking Geometry: Squares and Rhombi Worksheet Answers

When diving into the world of geometry, understanding shapes like squares and rhombi (rhombuses) is fundamental. These shapes, though similar, have distinct properties that can be explored in depth through various exercises. This blog post will guide you through a comprehensive worksheet focusing on squares and rhombi, complete with answers and explanations.
Introduction to Squares and Rhombi
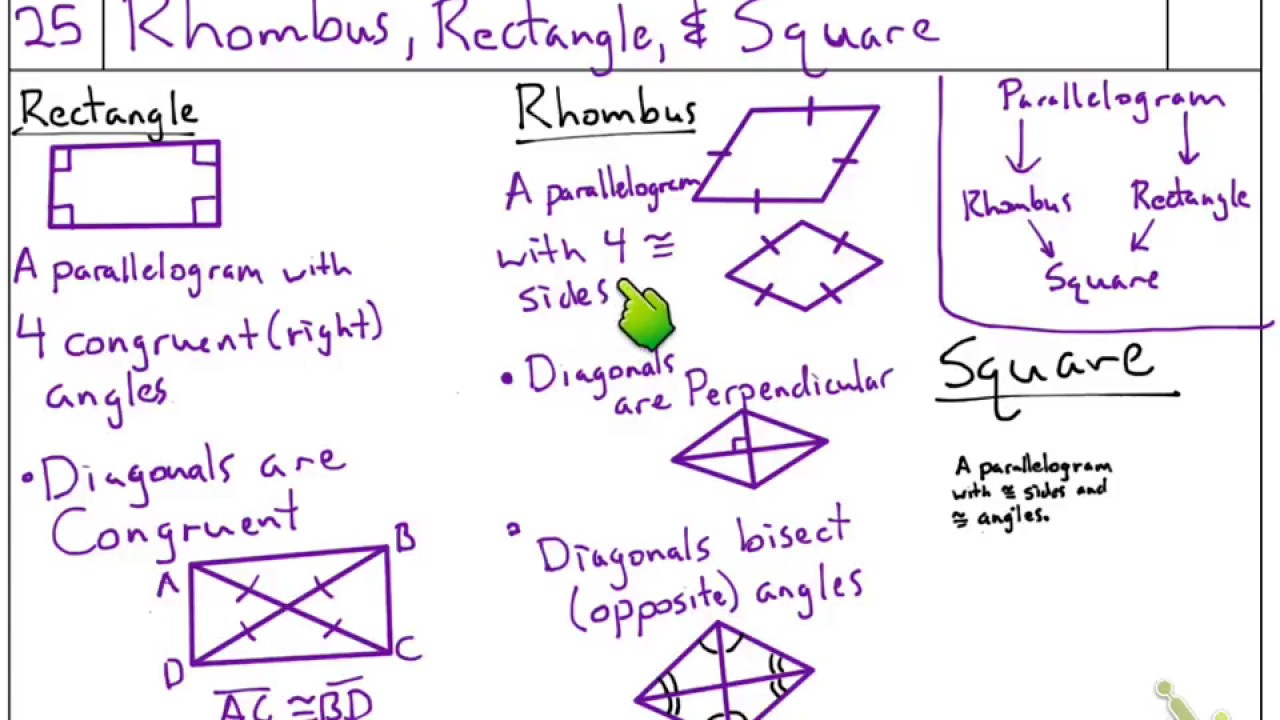
Before we jump into the worksheet, let’s recap some key characteristics of squares and rhombi:
- Squares: All sides are equal, all angles are 90 degrees, diagonals bisect each other at right angles, and the diagonals are equal in length.
- Rhombi: All sides are equal, opposite angles are equal, diagonals bisect each other at right angles, but the angles can vary.
Worksheet: Squares and Rhombi

Part 1: Basic Properties

Here are some questions to help identify the basic properties of squares and rhombi:
- Identify which shape is a square and which is a rhombus in the following diagrams:
- True or False: All rhombi are squares.
- What property do squares have that not all rhombi have?
 |
 |

Answer: The shape on the left is a square, and the shape on the right is a rhombus.
Answer: False. A rhombus with 90-degree angles is a square, but not all rhombi have this property.
Answer: Right Angles. Squares have all angles at 90 degrees, whereas rhombi do not necessarily have any right angles.
Part 2: Diagonals and Angles

Now let’s explore how diagonals and angles relate to squares and rhombi:
- What is the relationship between the diagonals of a square?
- Can the diagonals of a rhombus be of equal length?
- If one angle of a rhombus is 120 degrees, what are the other angles?
Answer: In a square, diagonals are equal in length and bisect each other at right angles.
Answer: Yes, but only if the rhombus is also a square. Otherwise, they might not be equal.
Answer: The opposite angle will also be 120 degrees, and the adjacent angles will be 60 degrees each, due to the sum of adjacent angles being 180 degrees.
Part 3: Calculations and Analysis

Let’s apply what we know with some practical calculations:
- Find the length of the diagonal of a square if one side measures 5 cm.
- A rhombus has diagonals measuring 8 cm and 6 cm. Find the side length of the rhombus.
Answer: Using the Pythagorean theorem in one quarter of the square, where the diagonal forms the hypotenuse, d = side × √2, so the diagonal is 5√2 cm.
Answer: The diagonals bisect each other at right angles, creating 4 right triangles. Here, half of each diagonal forms the legs of the triangles, so each side of the rhombus can be found using the Pythagorean theorem: side = √((8⁄2)^2 + (6⁄2)^2), which equals 5 cm.
Notes for Understanding

Geometry isn’t just about memorizing properties but also understanding how these properties interact. Here are some important notes:
🔍 Note: Always visualize the shape. Drawing helps to better understand how angles and lines interact.
📐 Note: Diagonals in a square always divide it into four congruent right triangles.
Final Thoughts

By going through this worksheet, you’ve engaged with the fundamental differences and similarities between squares and rhombi. This practice not only aids in recognizing these shapes but also in applying their geometric properties. From understanding the equality of sides to the relationships of diagonals and angles, you’ve unlocked key aspects of geometric shapes that can be applied beyond the worksheet to real-world applications in architecture, engineering, and design.
Can a square be considered a rhombus?

+
Yes, a square can be considered a rhombus because it has all sides equal in length. However, it has the additional property of all angles being right angles, which distinguishes it from most rhombi.
What makes a rhombus not a square?

+
A rhombus is not a square if its angles are not all 90 degrees. This lack of right angles is the key distinguishing feature.
How do the diagonals of a square and a rhombus differ?

+
The diagonals of a square are equal in length, bisect each other at right angles, and form congruent right triangles. In a rhombus, the diagonals are not necessarily equal (unless it’s a square) but still bisect each other at right angles.