5 Tips for Solving Square Root Problems Easily

Introduction to Square Roots

Understanding square roots is foundational in both mathematics and its real-world applications. At its essence, the square root of a number is a value that, when multiplied by itself, yields the original number. For instance, the square root of 25 is 5, because 5 times 5 equals 25. Despite appearing simple, square roots can pose challenges in various mathematical problems. Here are five practical tips to make solving these problems easier, enhancing your mathematical proficiency in a fun and educational way.
1. Know Your Perfect Squares

Mastering perfect squares is like learning the alphabet of mathematics. These are numbers whose square roots are whole numbers, forming the basis for understanding other square root calculations. Here's a quick list to memorize:
- 1: 12 = 1
- 4: 22 = 4
- 9: 32 = 9
- 16: 42 = 16
- 25: 52 = 25
- 36: 62 = 36
- 49: 72 = 49
- 64: 82 = 64
- 81: 92 = 81
- 100: 102 = 100
📝 Note: Memorize as many as you can, but focus on those frequently encountered in your calculations.
2. Use Estimation Techniques

Not every number has a perfect square root, but you can get close using estimation. Consider:
- Finding the two nearest perfect squares.
- For example, to estimate the square root of 52:
- 49 (72) is less than 52, but 64 (82) is more. Thus, √52 lies between 7 and 8.
- To refine the estimate, average the two numbers: (7 + 8) / 2 = 7.5
- If precision is needed, continue refining this initial estimate with further calculations.
3. Simplify Square Roots

When dealing with larger or more complex numbers, simplifying can reduce complexity:
- Break down the number into factors where one or more are perfect squares.
- E.g., √72:
- 72 = 36 * 2 (since 36 is a perfect square, √36 = 6)
- Thus, √72 = √36 * √2 = 6√2
- Recognizing this pattern can make calculations much more manageable.
4. Apply the Conjugate Pair Technique

In algebra, conjugate pairs are used to rationalize square root expressions:
- For expressions like (5 + √2), its conjugate is (5 - √2).
- Multiplying these will eliminate the square root in the denominator or numerator, simplifying your solution.
📚 Note: While this method is common in algebraic manipulation, it can also help in simplifying calculations involving square roots in other contexts.
5. Utilize Technology and Calculators

Despite the importance of manual calculation, don't underestimate the power of modern tools:
- Scientific calculators and mathematical software can give you exact or approximate square root values, enhancing accuracy and efficiency.
- Many mobile apps can also serve this purpose, often providing additional features like equation solving and graphing.
These tips for solving square root problems easily blend traditional math skills with modern technology, making the subject more approachable and less daunting. Whether you're preparing for an exam or just curious about numbers, these techniques will not only aid in solving square root problems but also deepen your mathematical understanding.
By mastering these tips, you're not only improving your problem-solving abilities in mathematics but also equipping yourself with tools to better understand and engage with numerical patterns and relationships in a wide variety of fields.
How can I improve my square root calculation speed?
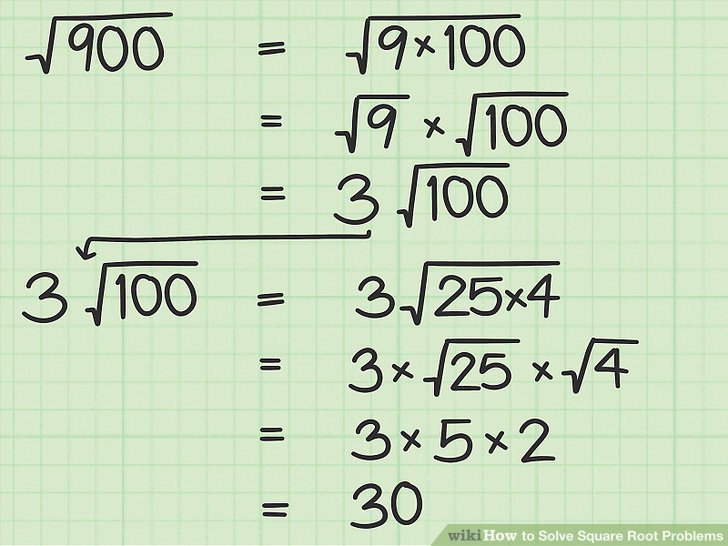
+
Practice regularly, utilize memory aids for perfect squares, and get familiar with estimation techniques to enhance your speed.
Is it useful to know the square roots of numbers beyond 100?

+
Absolutely, especially in fields like engineering, physics, and higher mathematics, where larger numbers and their roots frequently come into play.
Can understanding square roots help in fields other than mathematics?

+
Yes, square roots are fundamental in areas like architecture, finance for calculating returns on investments, and even in computer science for data structures and algorithms.