Mastering Square Roots and Cube Roots Easily

Understanding the basic mathematical concepts like square roots and cube roots can seem daunting at first, especially if you're not particularly inclined towards math. However, with the right approach and some simple tricks, these concepts become not only manageable but also quite fascinating. In this comprehensive guide, we'll delve into the realm of square roots and cube roots, demystifying these operations and providing you with practical techniques to master them easily.
The Fundamentals of Square Roots

Before we dive into tricks and tips, let’s ensure we understand what a square root is:
- A square root of a number x is a value that, when multiplied by itself, gives the number x.
- The square root of x is denoted mathematically as √x, where √ is the radical symbol.
Why Learn Square Roots?

Learning square roots isn’t just about solving equations; it’s integral to various real-world applications:
- Geometry: Calculating the side length of a square from its area.
- Physics: Determining distances in kinematics.
- Computer Graphics: Creating realistic shadows, reflections, and lighting effects.
Estimating Square Roots Manually
If you’re not using a calculator, here’s how you can estimate the square root of a number:
- Find the nearest perfect squares: Identify the perfect squares (1, 4, 9, 16, 25, 36, etc.) surrounding the number in question.
- Interpolation: Use the known square roots of these perfect squares to estimate the square root of the number you want to find. For example, to find √12:
- 9 (√9 = 3) and 16 (√16 = 4) are the nearest perfect squares.
- Since 12 is closer to 16 than 9, the square root of 12 will be a bit less than 4 but more than 3. Let’s estimate it as 3.5.
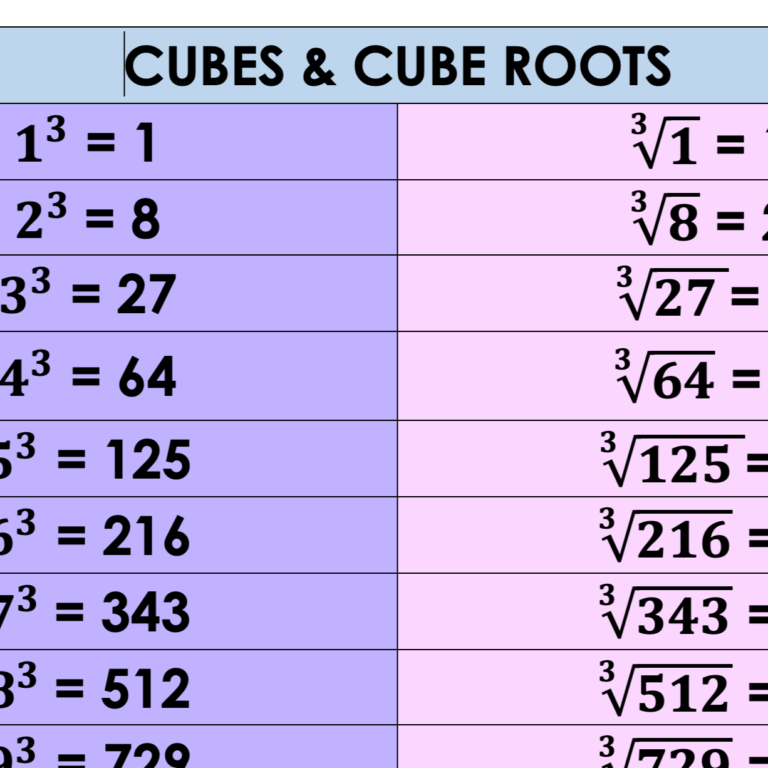
Mastering Cube Roots

Similar to square roots, cube roots also have their own allure. Here’s what you need to know:
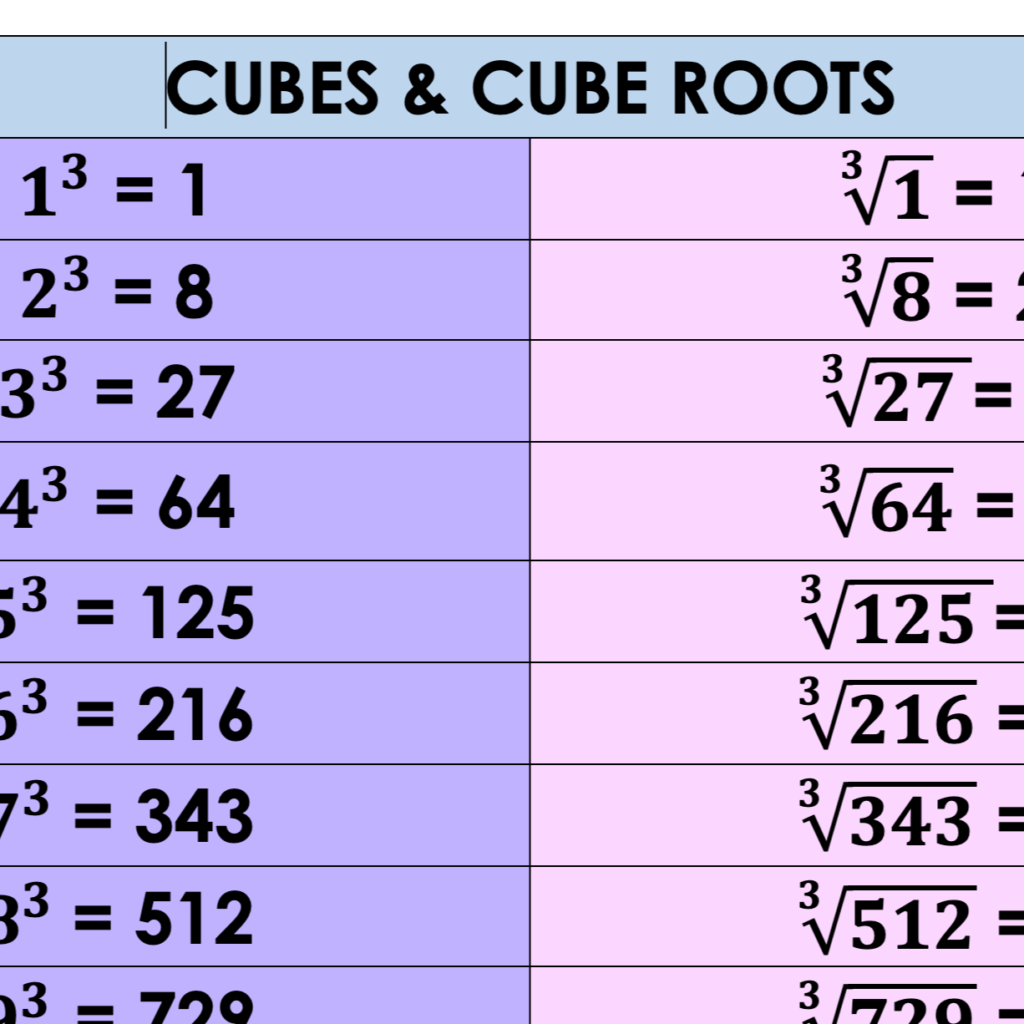
- A cube root of a number x is a value that, when raised to the third power (x³), gives the number x.
- It’s symbolized as ³√x in mathematics.
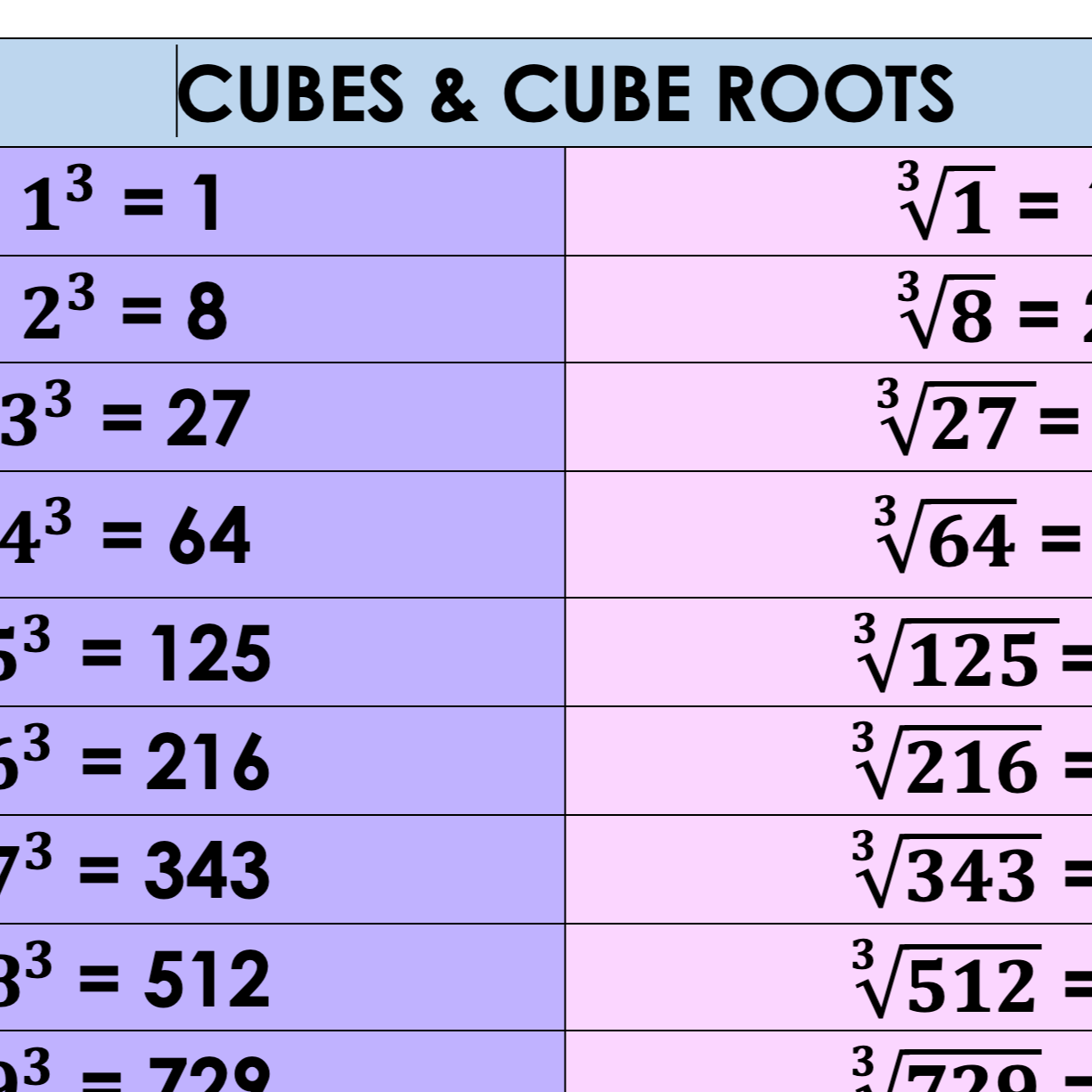
The Importance of Cube Roots
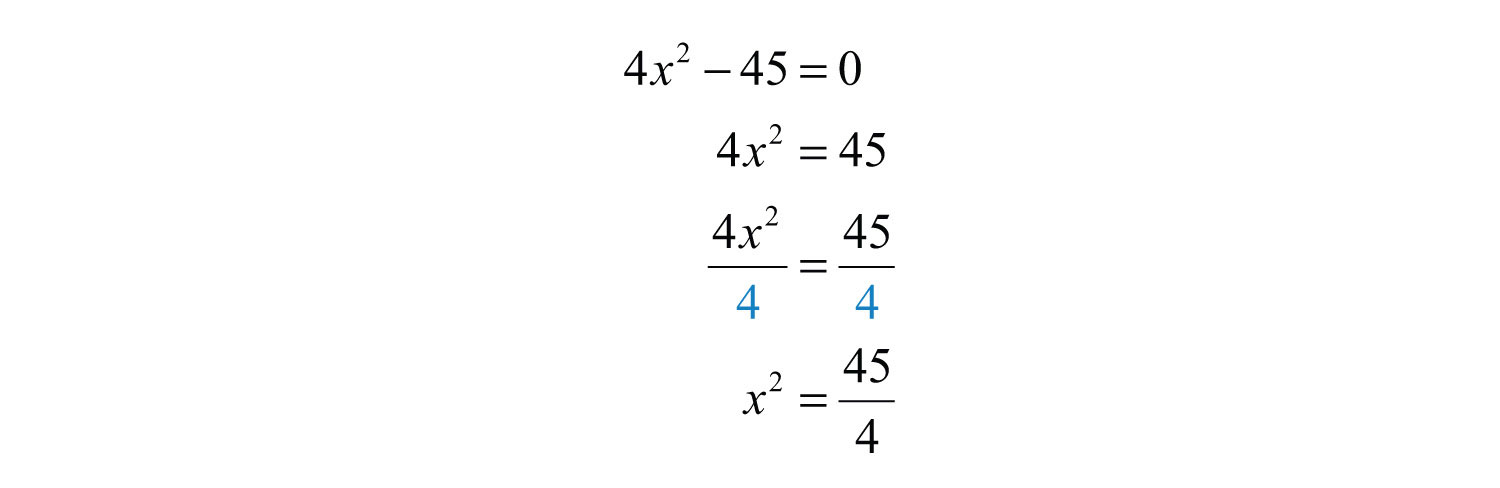
Understanding cube roots has several practical applications:
- Engineering: Determining the volume of cubic structures.
- Science: Calculating distances in space-time calculations.
- Finance: Estimating future values in compound interest scenarios.
Finding Cube Roots
Like square roots, you can estimate cube roots manually:
- Find the nearest perfect cubes: Know the cubes of integers (1, 8, 27, 64, 125, etc.) closest to your number.
- Interpolation: Use these to guess the cube root. For instance, to estimate ³√50:
- 27 (³√27 = 3) and 64 (³√64 = 4) are the nearest perfect cubes.
- As 50 is closer to 64, its cube root will be slightly less than 4 but more than 3. An educated guess might be 3.6 or 3.7.
Tricks and Techniques for Quick Estimation

Here are some useful techniques to simplify your work with roots:
- The Digit-by-Digit Method: For square roots, you can use a systematic method to find digits one by one, refining your answer as you go. Start by finding the largest integer whose square is less than or equal to the number you’re working with, then continue with smaller units.
- The Binary Search Method: For both square and cube roots, you can use binary search to quickly narrow down the range. If you know the root is between two numbers, you keep calculating the midpoint until you get close enough.
Using Digital Tools

While we’re focusing on mental calculation and understanding, it’s worth mentioning:
- Calculators: Most scientific and graphing calculators have functions to find roots quickly.
- Software: Tools like Excel, Google Sheets, or Python (with libraries like NumPy) can perform these calculations automatically.
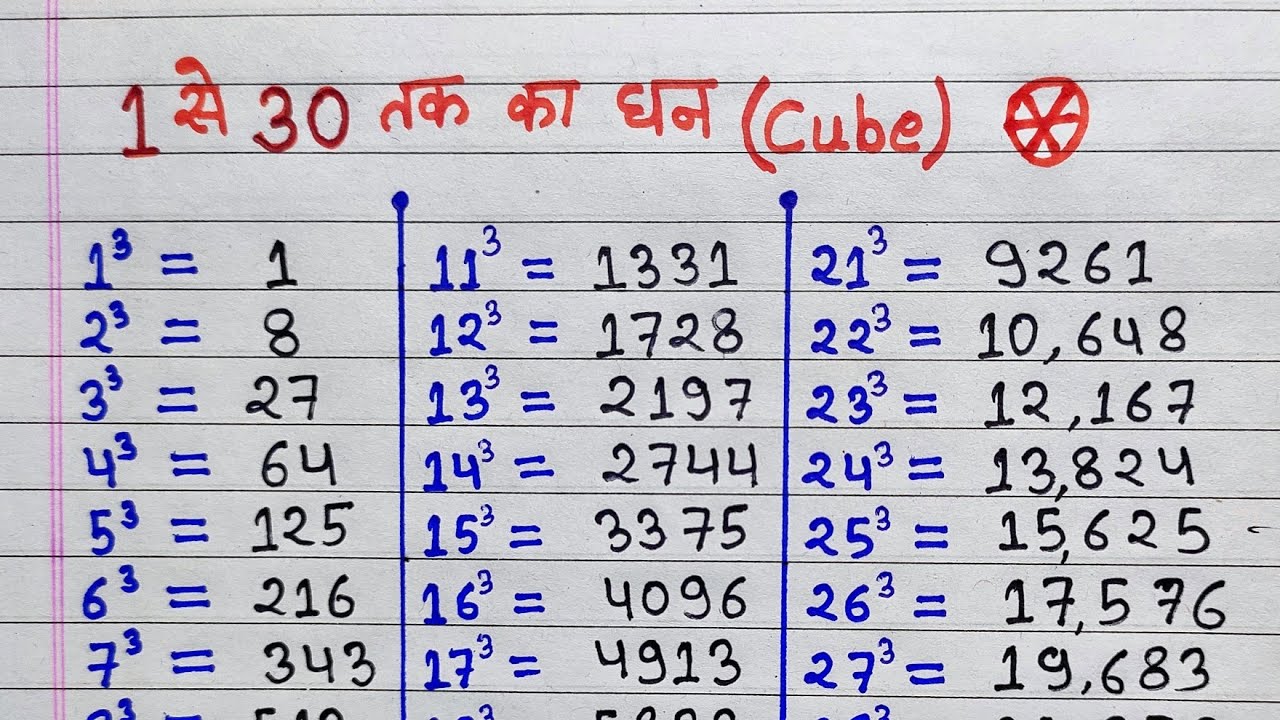
Mastering Roots Through Practice
To truly master square and cube roots:
- Practice regularly with different numbers.
- Learn the square and cube of integers from 1 to 15; knowing these offhand will help immensely with estimation.
- Use flashcards or apps designed for math practice.
- Work through real-world problems or puzzles that require root calculations.
Tips for Memorization

Here are some memory aids:
- Create mnemonic devices or rhymes for perfect squares and cubes.
- Link numbers with visuals, like imagining cubes for cube roots or squares for square roots.
💡 Note: Consistent practice is key to internalizing these mathematical skills.
As we've explored, mastering square roots and cube roots involves understanding their mathematical significance, learning estimation techniques, and practicing regularly. These skills are not only useful in academic settings but also have numerous applications in real-life scenarios. Remember, while tools can expedite calculations, the true mastery lies in understanding the concept deeply and being able to estimate without them. By combining mental techniques with practical application, you'll be well on your way to easily mastering roots.
What are some practical uses of square roots in everyday life?
+
Square roots are often used in calculating areas and dimensions in home improvement projects, estimating distances in physics problems, and determining the price or quantity of goods when dealing with proportional scaling.
Can I always estimate roots without a calculator?

+
Yes, you can estimate roots without a calculator, especially for numbers close to known perfect squares or cubes. However, accuracy decreases for very large numbers or when high precision is needed.
How can I make root calculations fun for kids?

+
By incorporating games or puzzles, using visual aids like cubes or square tiles to physically demonstrate squares and cubes, or even coding simple games that involve root calculations.