Special Triangles Worksheet: Mastering Geometry with Ease
Understanding Special Triangles

Special triangles are a fundamental concept in geometry, and mastering them can make a huge difference in solving various problems. In this article, we will explore the world of special triangles, their properties, and how to use them to solve problems with ease.
What are Special Triangles?

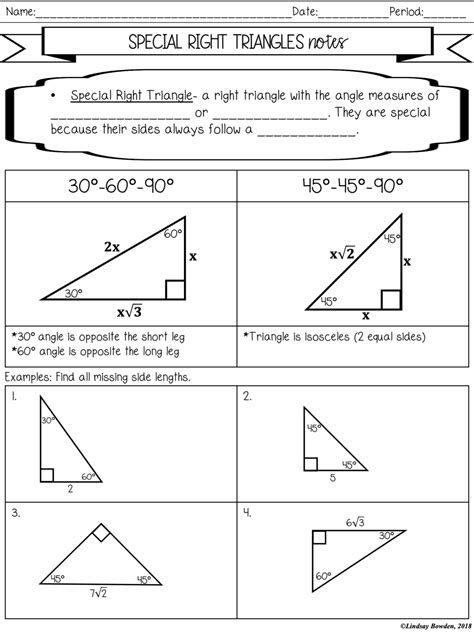
Special triangles are triangles that have unique properties that make them easier to work with. These triangles are used to solve problems involving angles, sides, and trigonometric functions. The most common special triangles are the 30-60-90 triangle and the 45-45-90 triangle.
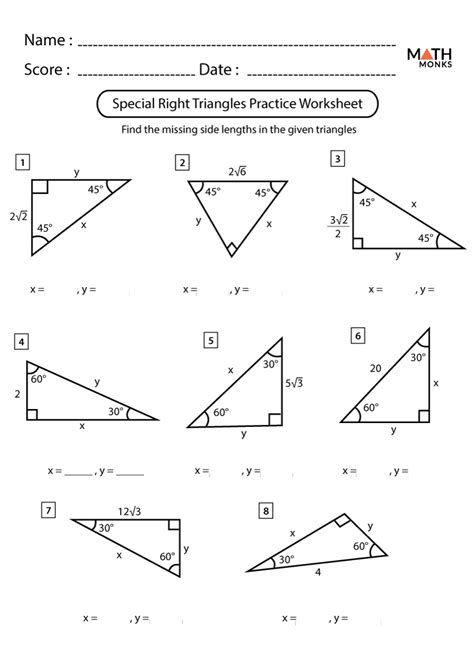
30-60-90 Triangle
A 30-60-90 triangle is a triangle with angles measuring 30, 60, and 90 degrees. The side opposite the 30-degree angle is half the length of the hypotenuse, and the side opposite the 60-degree angle is 3⁄2 times the length of the side opposite the 30-degree angle.
| Angle | Opposite Side |
|---|---|
| 30° | x |
| 60° | x√3 |
| 90° | 2x |

45-45-90 Triangle

A 45-45-90 triangle is a triangle with two angles measuring 45 degrees and one angle measuring 90 degrees. The two sides opposite the 45-degree angles are equal and the hypotenuse is √2 times the length of either side.
| Angle | Opposite Side |
|---|---|
| 45° | x |
| 45° | x |
| 90° | x√2 |
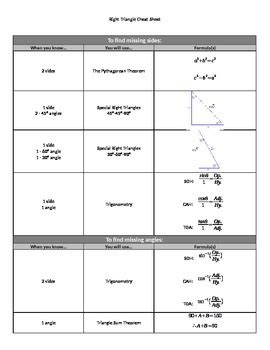
How to Use Special Triangles
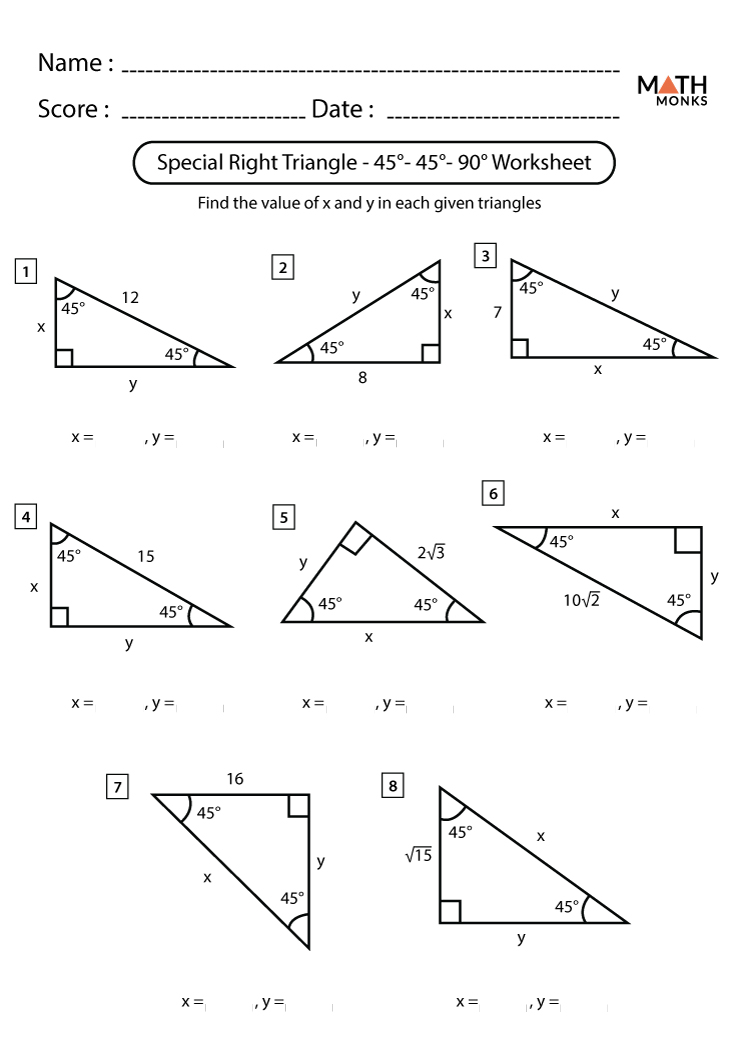
Special triangles can be used to solve various problems involving angles, sides, and trigonometric functions. Here are some examples:
- Finding the length of a side: If you know the length of one side of a special triangle, you can use the properties of the triangle to find the length of the other sides.
- Finding the measure of an angle: If you know the length of the sides of a special triangle, you can use the properties of the triangle to find the measure of the angles.
- Solving trigonometric functions: Special triangles can be used to solve trigonometric functions such as sine, cosine, and tangent.
📝 Note: Special triangles are used to solve problems in various fields such as physics, engineering, and architecture.
Example Problems

Here are some example problems that can be solved using special triangles:
- Find the length of the hypotenuse of a 30-60-90 triangle with a side opposite the 30-degree angle measuring 5 inches.
- Find the measure of the angle opposite a side measuring 3 inches in a 45-45-90 triangle with a hypotenuse measuring 6 inches.
- Solve the equation sin(x) = 1⁄2 using a special triangle.
Conclusion
Mastering special triangles can make a huge difference in solving various problems involving angles, sides, and trigonometric functions. By understanding the properties of special triangles, you can solve problems with ease and accuracy. Remember to practice using special triangles to solve problems and you will become proficient in no time.
What is the difference between a 30-60-90 triangle and a 45-45-90 triangle?

+
A 30-60-90 triangle has angles measuring 30, 60, and 90 degrees, while a 45-45-90 triangle has two angles measuring 45 degrees and one angle measuring 90 degrees.
How can I use special triangles to solve trigonometric functions?

+
Special triangles can be used to solve trigonometric functions by using the properties of the triangle to find the length of the sides and the measure of the angles.
What are some real-world applications of special triangles?

+
Special triangles have various real-world applications in fields such as physics, engineering, and architecture.
Related Terms:
- Special triangles worksheet answer key
- Special triangles worksheet pdf
- special right triangles worksheet 45 45 90
- Special Right Triangles answer Key
- special right triangle practice problems
- special right triangles cheat sheet



