5 Key Segments in Triangles: Worksheet Guide

Understanding triangle segments is fundamental in geometry, offering insights into the properties and measurements that make triangles unique. From the basic sides and angles to the more complex medians, altitudes, perpendicular bisectors, angle bisectors, and circumcenters, each segment plays a pivotal role in triangle analysis. This worksheet guide will delve into the five key segments in triangles, providing a structured approach to understanding these concepts, their definitions, and their applications.
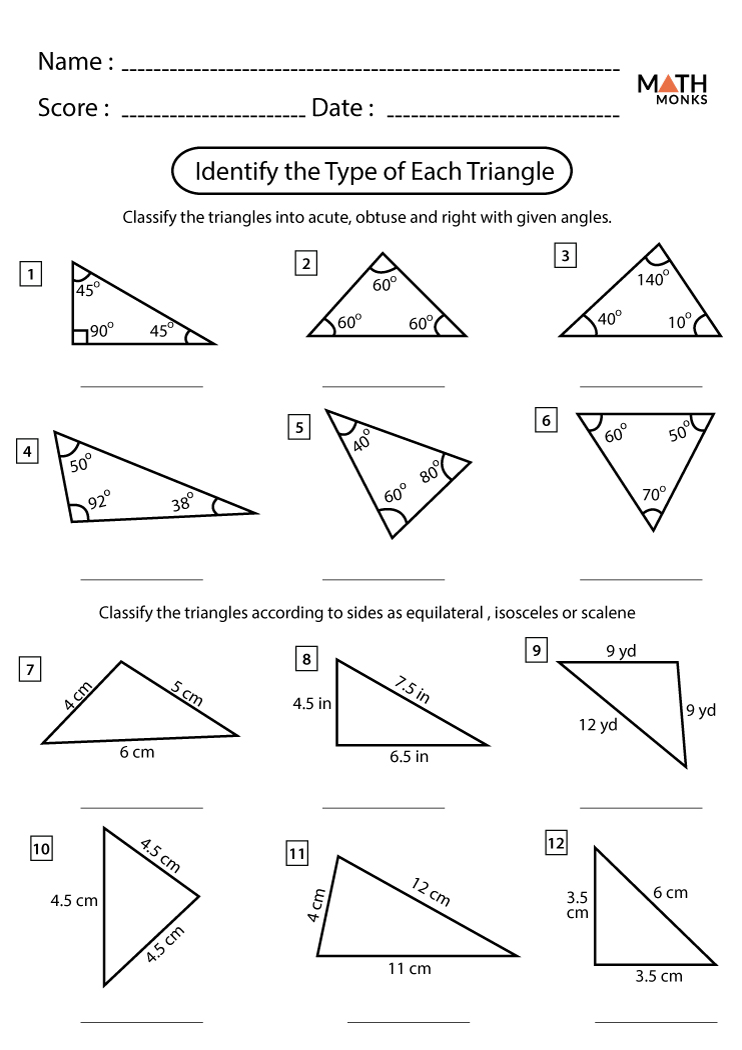
1. Sides and Angles

Before diving into the more intricate segments, it’s essential to review the fundamentals:
- Side Lengths: The distances between each vertex in a triangle.
- Angles: The measures of the interior angles of a triangle.

Key Takeaways:
- The sum of the angles in any triangle is always 180 degrees.
- Each side is opposite to an angle; the longer the side, the larger the opposite angle.
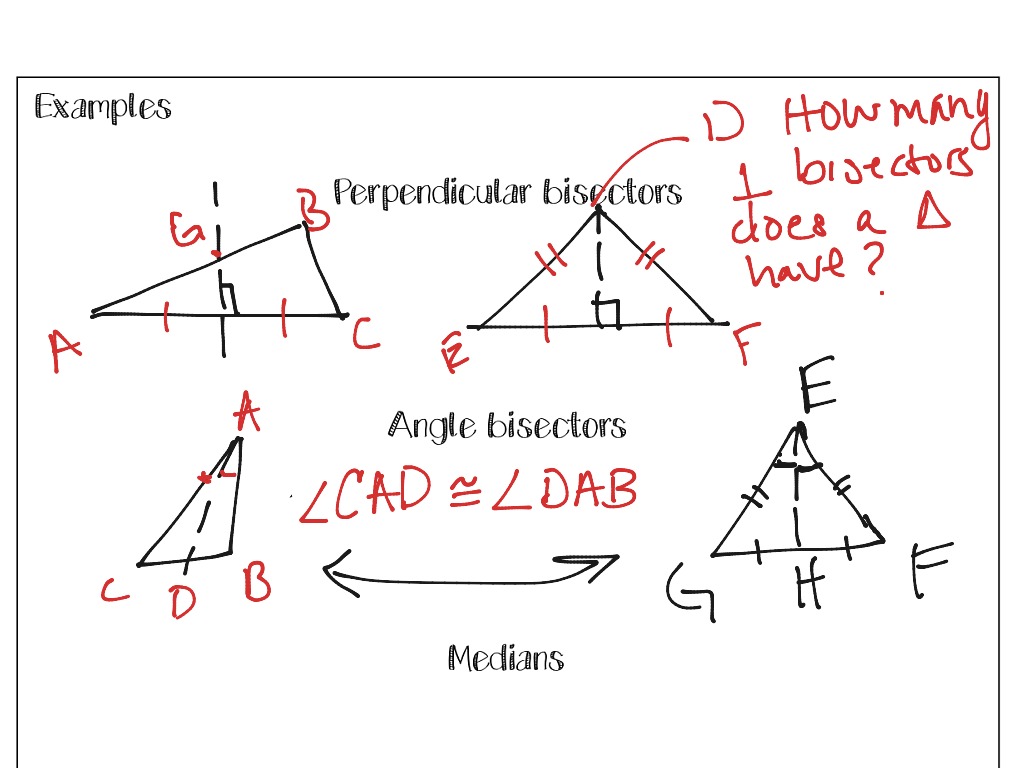
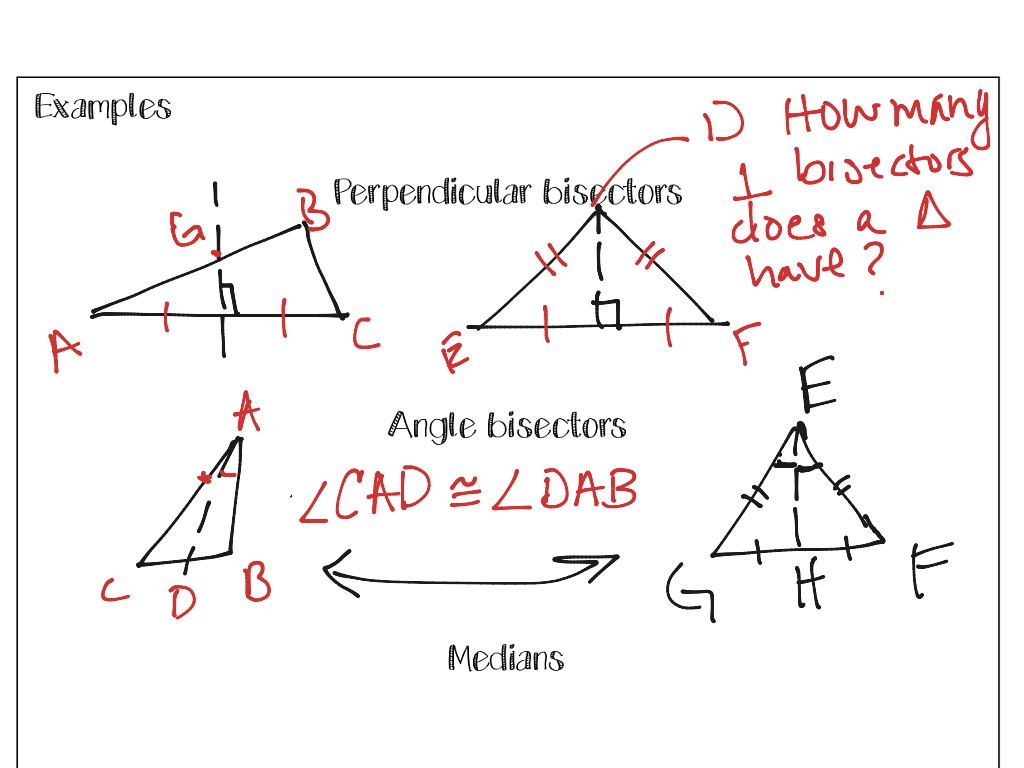
2. Medians

Medians are line segments drawn from a vertex to the midpoint of the opposite side:
- Every triangle has three medians, and they all intersect at the centroid.
- The centroid is also known as the center of gravity.

Key Takeaways:

- Medians divide the triangle into two equal areas.
- The centroid is always 2⁄3 of the way along each median from the vertex to the midpoint.
3. Altitudes

Altitudes are perpendicular lines from a vertex to the opposite side (or extended side in obtuse triangles):
- Three altitudes in each triangle intersect at the orthocenter.

Key Takeaways:

- In a right triangle, the legs are altitudes, and the orthocenter is at the right angle vertex.
- In an obtuse triangle, one altitude lies outside the triangle.
4. Perpendicular Bisectors

Perpendicular bisectors are lines that intersect the sides of a triangle at their midpoints and are perpendicular to them:
- All three bisectors converge at the circumcenter.

Key Takeaways:
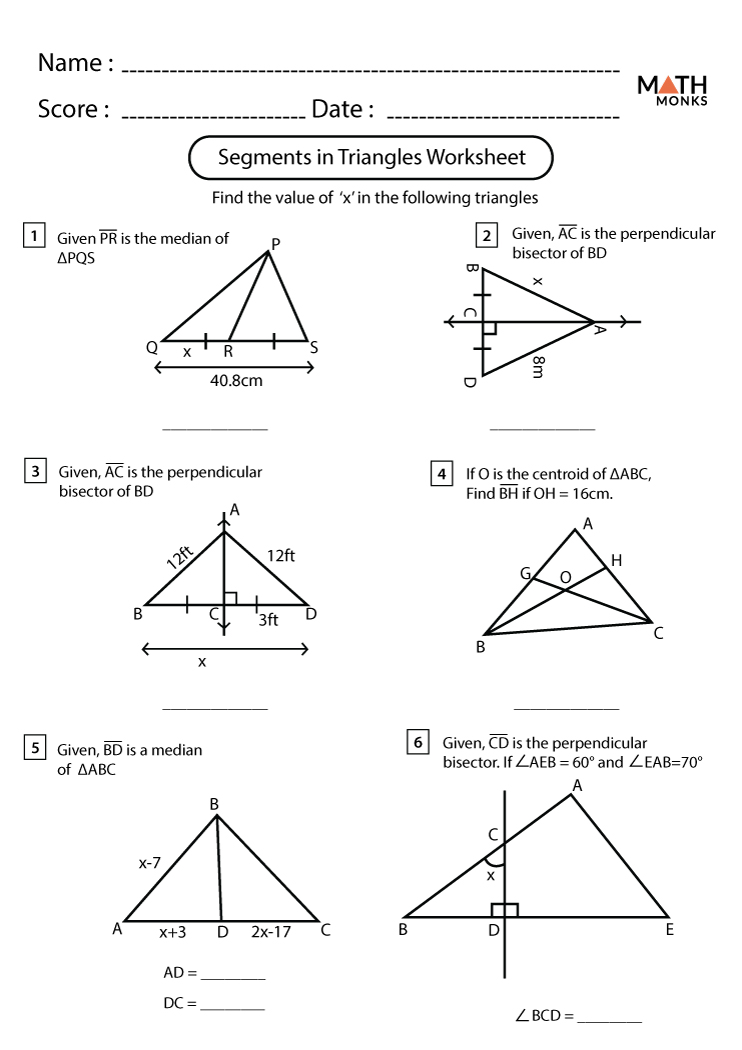
- The circumcenter is equidistant from all three vertices, forming the center of the circumscribed circle.
5. Angle Bisectors
Angle bisectors split each angle into two equal parts:
- All three angle bisectors meet at the incenter.

Key Takeaways:

- The incenter is the center of the inscribed circle or incircle.
- It is equidistant from the sides of the triangle.
By mastering these five key segments, you gain a deeper understanding of triangles, their properties, and how they interact with one another. This knowledge not only serves educational purposes but also has practical applications in fields like engineering, architecture, and computer graphics. Understanding how these segments work within triangles allows for better analysis, design, and problem-solving in real-world scenarios.
What is the difference between a median and an altitude in a triangle?

+
A median in a triangle is a line segment from a vertex to the midpoint of the opposite side, dividing it into two equal areas. An altitude, however, is a perpendicular line from a vertex to the opposite side or extended side, not necessarily dividing the area equally. The key difference is their endpoints and purpose; medians focus on length and area division, while altitudes emphasize perpendicularity.
Why is the centroid important in triangle analysis?

+
The centroid, or center of gravity, is where all three medians intersect. It’s crucial because it represents the balancing point of a triangle. This point divides each median into a ratio where two-thirds of the segment is from the vertex to the centroid, and one-third from the centroid to the midpoint, useful in balancing, stability, and centroidal triangulation.
How does understanding triangle segments help in real-world applications?
+
Understanding triangle segments aids in various fields like architecture for designing stable structures, in engineering for stress analysis, in computer graphics for rendering accurate shapes, and in navigation for calculating distances and positions using trilateration. These principles help professionals and students alike in problem-solving and optimizing designs for functionality and efficiency.


