5 Must-Know Answers for Circle Segments Worksheet

The study of geometric shapes forms an essential part of mathematical education, helping students develop logical thinking and problem-solving skills. Among these shapes, the circle segment stands out due to its complex yet intriguing nature. In this detailed post, we will delve into five must-know answers for circle segments worksheet problems, offering insight into how you can tackle these with ease.
Understanding Circle Segments
A circle segment refers to the region bounded by a chord and the arc subtending this chord. Segments can be categorized into two main types:
- Minor Segment: The smaller area enclosed by the chord and the arc.
- Major Segment: The larger area that includes the remaining part of the circle after the minor segment is subtracted.
To fully grasp circle segments, you need to understand:
- The properties of the circle.
- How to find the segment length or arc length.
- Formulas for calculating the area of the segment.
1. How to Calculate the Length of a Chord
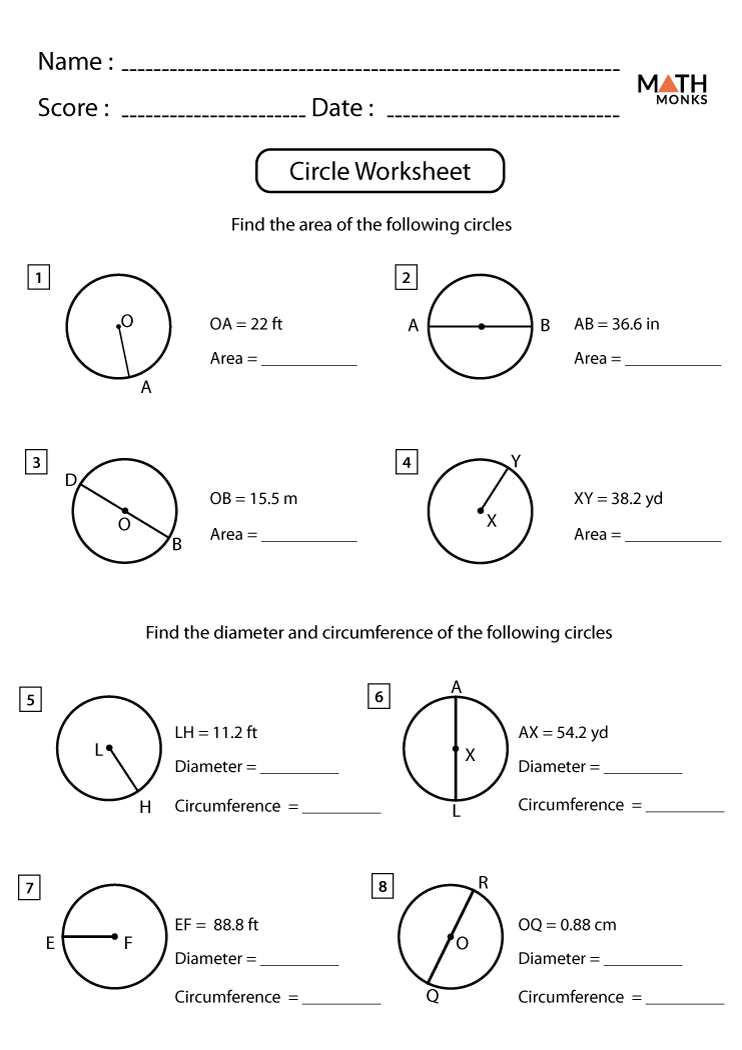
The chord length of a circle can be calculated if you know the radius and the perpendicular distance from the center to the chord. Here’s the formula:
[ \text{Chord Length} = 2 \times \sqrt{r^2 - d^2} ]
Where:
- r is the radius of the circle
- d is the perpendicular distance from the center to the chord
Important note:
🚫 Note: Remember, this formula assumes the perpendicular distance is measured from the center to the chord.
2. Determining the Arc Length and Area of a Segment

To find the arc length and area of a circle segment:
- Arc Length: L = \theta \times r , where \theta is in radians.
- Area of the Segment: \[ A = \frac{1}{2}r^2(\theta - \sin\theta) \]
This formula uses the central angle \theta in radians. You must convert degrees to radians if given in degrees:
[ \text{Radians} = \frac{\text{Degrees} \times \pi}{180} ]
Here’s a table to help you understand the conversion:
| Degrees | Radians |
|---|---|
| 30° | \frac{\pi}{6} |
| 45° | \frac{\pi}{4} |
| 60° | \frac{\pi}{3} |
| 90° | \frac{\pi}{2} |

3. Application of Circle Segment Properties in Real Life

Circle segments have numerous applications in the real world. Here are a few examples:
- Engineering: Designing curves in roads, bridges, and tunnels.
- Agriculture: Understanding the spread of crops or irrigation systems in circular fields.
- Art and Architecture: Drawing arches and domes.
4. The Importance of Knowing Segment Area in Geometry

The area of a segment provides valuable insights into:
- Volume calculations in 3D shapes with curved surfaces.
- Land surveying, where plots of land might not be perfectly rectangular.
5. Solving Complex Circle Segment Problems

For students, complex problems often involve multiple segments or require geometric reasoning. Here's how to approach them:
- Identify known variables (radius, chord length, arc length, etc.)
- Sketch the problem to visualize the segments.
- Use trigonometry and circle formulas to solve for unknown quantities.
- Validate your solution by checking if it aligns with the problem's constraints.
In wrapping up, understanding circle segments goes beyond mere memorization of formulas. It's about applying these principles to solve real-world problems, enhancing both your mathematical and critical thinking skills. Knowing how to find chord length, arc length, and segment area not only enriches your geometry knowledge but also equips you for practical applications in various fields.
What is the difference between a sector and a segment of a circle?

+
A sector is a region bounded by two radii and the arc, whereas a segment is bounded by a chord and the arc. A segment includes part of the sector.
How do you convert degrees to radians?

+
To convert degrees to radians, use the formula: ( \text{Radians} = \frac{\text{Degrees} \times \pi}{180} ).
Can you calculate the area of a segment if you only know the chord length?

+
No, to find the area of a segment, you need either the radius and central angle or the radius and the perpendicular height from the center to the chord.



