5 Key Problems for Special Right Triangles Explained

Understanding special right triangles is crucial for students of geometry and anyone interested in the mathematical foundations of various fields. Special right triangles are not just random triangles; they possess unique ratios and properties that make problem-solving and calculations much easier. In this post, we'll delve into five common problems associated with special right triangles, providing detailed explanations and solutions to enhance your understanding.
1. Identifying Special Right Triangles
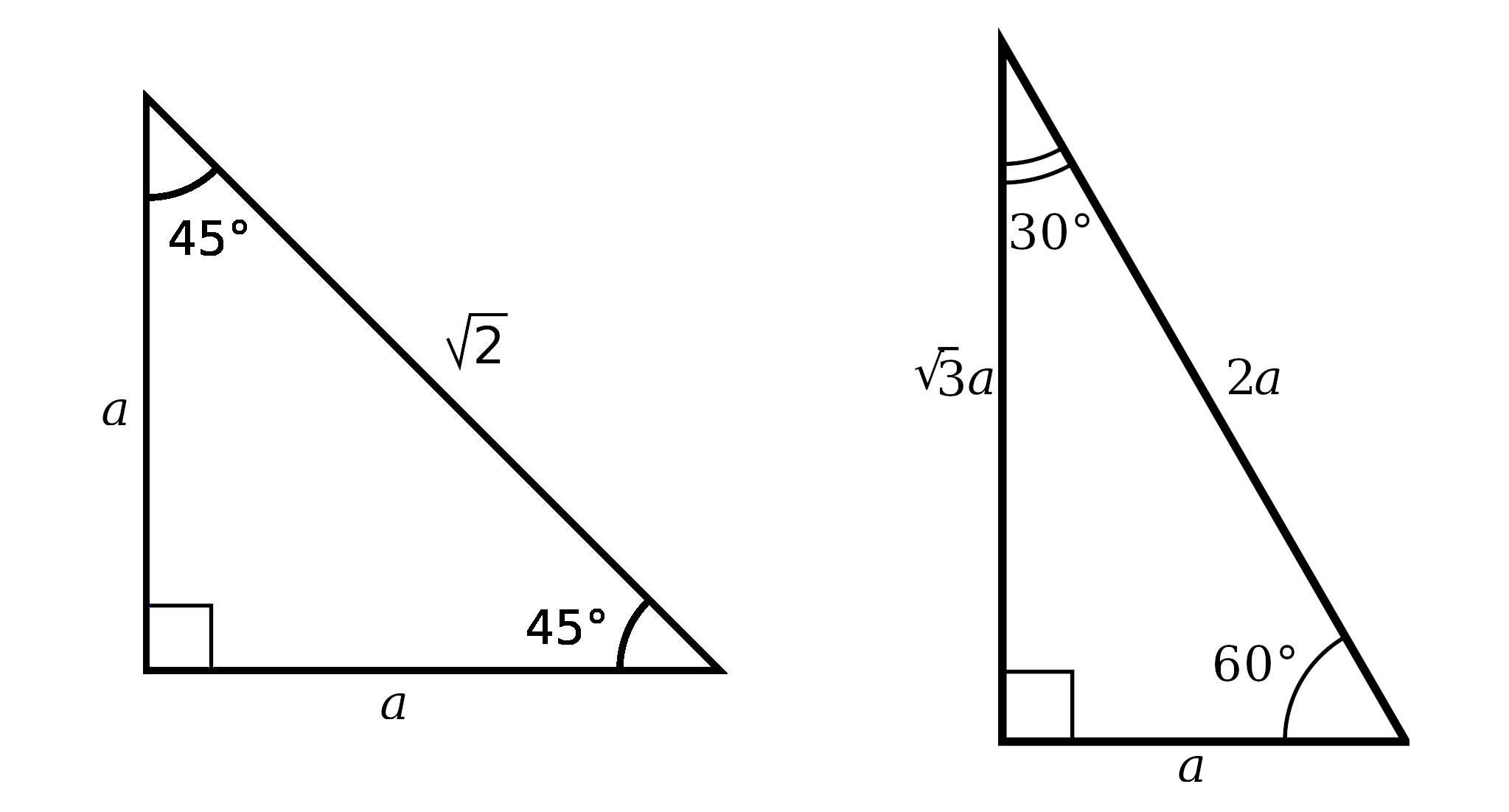

The first problem many encounter is identifying when a triangle is a special right triangle:
- Isosceles Right Triangle (45-45-90): If two sides of a triangle are equal and one angle is 90 degrees, it's a 45-45-90 triangle.
- 30-60-90 Triangle: A right triangle with an angle measuring 30 degrees or 60 degrees falls into this category. One side is half the hypotenuse.
2. Calculating Ratios in Special Right Triangles


The ratios of the sides of special triangles are specific:
- 45-45-90 Triangle:
- Side : Side : Hypotenuse = x : x : x√2
- 30-60-90 Triangle:
- Side : Side : Hypotenuse = x : x√3 : 2x
⚠️ Note: These ratios are fundamental in solving problems involving special right triangles. Always remember them for quick calculations.
3. Problem: Finding Missing Angles and Sides

One frequent challenge is determining unknown sides or angles:
- 45-45-90 Triangle: If one leg is 6 cm, the other leg is also 6 cm, and the hypotenuse would be 6√2 cm.
- 30-60-90 Triangle: If the hypotenuse is 10 cm, the shortest side (opposite the 30° angle) is 5 cm, and the longest leg is 5√3 cm.
📝 Note: Use trigonometry or Pythagorean theorem for triangles not matching these ratios or when needing exact values.
4. Trigonometric Functions in Special Triangles

Applying trigonometric functions:
| Angle | Sine (sin) | Cosine (cos) | Tangent (tan) |
|---|---|---|---|
| 30° | 1⁄2 | √3/2 | √3/3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1⁄2 | √3 |

5. Applications in Real-Life Problems


Special triangles are not just theoretical; they’re used in:
- Navigation and surveying for calculating distances and heights
- Architecture to design building structures and analyze stability
- Engineering for stress analysis and material strength testing
💡 Note: Recognizing these triangles in real-world scenarios can simplify complex problems into straightforward solutions.
In summary, recognizing and understanding the properties of special right triangles can significantly simplify geometric problem-solving. From identifying these triangles to applying their unique ratios and trigonometric functions, mastering these concepts offers a powerful tool for students and professionals alike. This knowledge not only enhances your geometric understanding but also provides a versatile approach to real-life applications where precision and efficiency are crucial.
Why are these triangles called ‘special’?

+
The term ‘special’ refers to the unique angles and side ratios these triangles possess, making calculations predictable and straightforward.
How do I remember the ratios of special triangles?

+
Many students use mnemonics or simple visualizations to remember ratios. For instance, for a 45-45-90 triangle, imagine an isosceles triangle with legs equal to x, and the hypotenuse is x√2.
Can special right triangles be used in trigonometry?

+
Absolutely! Their specific angles and ratios provide a perfect basis for understanding and applying trigonometric functions in practical and theoretical contexts.