5 Proven Tricks to Solve Special Triangles Fast

Mathematics often presents students and professionals with a variety of geometric puzzles, and among these, special triangles hold a distinct allure due to their unique properties and the challenges they pose. Whether you are preparing for an exam or dealing with geometric problems in real life, understanding how to quickly and efficiently solve special triangles can save you time and reduce stress. Here, we explore five proven tricks to tackle these triangles with ease.
Understanding Special Triangles

Before diving into the tricks, it’s crucial to understand what special triangles are:
- Equilateral Triangle: All sides are of equal length, and all angles are 60°.
- Isosceles Right Triangle: Two sides are equal with one angle at 90°.
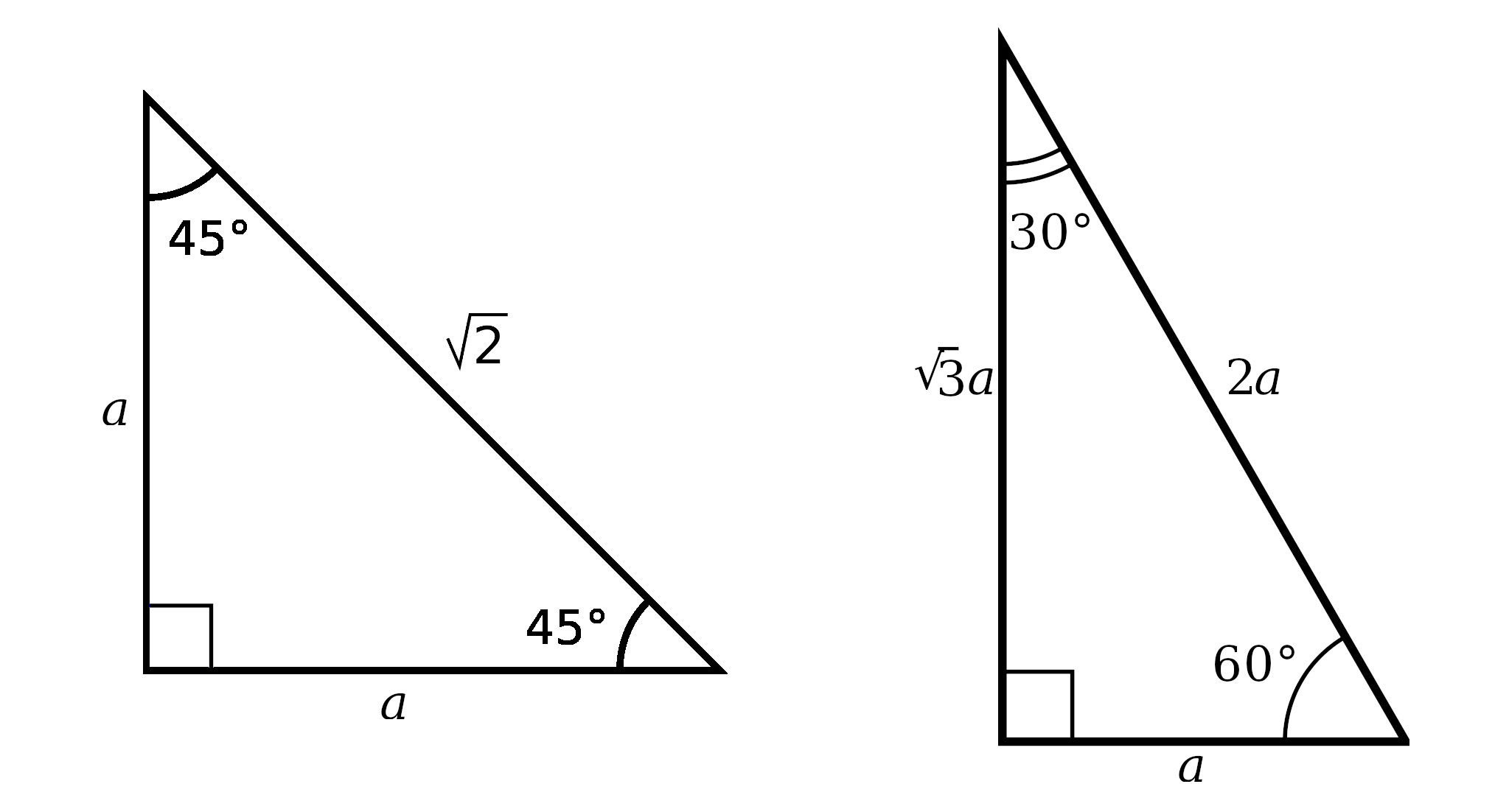
- 30-60-90 Triangle: A triangle with angles of 30°, 60°, and 90° where the sides are in a ratio of
1:√3:2. - 45-45-90 Triangle: Two equal angles of 45° with a ratio of sides
1:1:√2.
Trick 1: Using Pythagorean Theorem with Special Ratios

One of the most straightforward methods to deal with right-angled special triangles is through the application of the Pythagorean theorem:
a² + b² = c², where a and b are the legs, and c is the hypotenuse.
- For a 45-45-90 triangle, if one leg is x, then the hypotenuse is x√2.
- For a 30-60-90 triangle, if the shorter leg is x, then the hypotenuse is 2x and the longer leg is x√3.
By recognizing these ratios, you can immediately deduce the lengths of the other sides without additional calculations.
🔍 Note: This trick works best when you know at least one side of the triangle.

Trick 2: The Angle Bisector Property

For isosceles triangles, bisecting the vertex angle will split the triangle into two congruent right triangles. This can simplify calculations:
- Bisect an angle to form two right triangles where you can apply the properties of 45-45-90 or 30-60-90 triangles.
- The bisector of an angle in an isosceles triangle will also bisect the opposite side, providing symmetry and making the calculations easier.
Trick 3: Side Ratios for Quick Calculation

Understanding the fixed ratios in special triangles can be your quickest solution:
| Triangle Type | Side Ratios |
|---|---|
| 30-60-90 | 1:√3:2 |
| 45-45-90 | 1:1:√2 |

With these ratios, you can calculate the remaining sides of the triangle almost instantly. For instance, if you know the hypotenuse of a 30-60-90 triangle, you can find the shorter and longer legs directly.
🔎 Note: Always check if the triangle fits into one of these specific categories before applying this trick.
Trick 4: Trigonometry to Determine Lengths

For non-right triangles or when dealing with angles that are not standard in special triangles, trigonometry comes in handy:
- Use
sin(θ),cos(θ), andtan(θ)to find missing sides or angles. - Sine Rule:
a/sin(A) = b/sin(B) = c/sin© - Cosine Rule:
c² = a² + b² - 2ab cos©
These formulas are especially useful when one or more angles are known.
🚩 Note: Trigonometry might take longer but is invaluable for more complex triangle problems.
Trick 5: Construction and Properties

Sometimes, understanding how to construct special triangles can provide quick solutions:
- For an equilateral triangle, construct one by drawing an angle bisector, which splits it into two 30-60-90 triangles.
- Use geometric constructions to understand properties like the circumcircle or incircle of triangles, which can help find sides or angles indirectly.
Geometry is not just about solving equations; visual recognition of shapes and their properties can often provide shortcuts.
In summary, tackling special triangles efficiently involves recognizing their distinct properties and applying the right method for the situation. The five tricks discussed—using Pythagorean theorem with ratios, angle bisectors, side ratios, trigonometry, and geometric construction—can significantly streamline your problem-solving process. By mastering these techniques, you'll find yourself approaching geometric challenges with newfound confidence, whether you're solving a math problem or designing an architectural model.
What is the difference between an equilateral and an isosceles triangle?
+
An equilateral triangle has all sides of equal length and all angles equal to 60°, while an isosceles triangle has at least two sides of equal length with the angles opposite those sides also being equal.
Can I use the Pythagorean theorem for all triangles?

+
No, the Pythagorean theorem applies only to right-angled triangles. However, for other triangles, you can use the cosine rule or the law of sines to find sides and angles.
Why are special triangles important in mathematics?

+
Special triangles have unique properties that make geometric calculations simpler and more straightforward. They are often foundational in trigonometry, physics, engineering, and architecture due to their predictable ratios and angles.
How can I quickly identify a special triangle?

+
Look for side length ratios or angle measurements that match those of known special triangles. For instance, if one angle is 90°, check if the other angles and side lengths fit the patterns of 30-60-90 or 45-45-90 triangles.